- Kontinuierliche Fourier-Transformation
-
Die kontinuierliche Fourier-Transformation ist eine Form der Fourier-Transformation (FT), die es erlaubt, kontinuierliche, aperiodische Vorgänge in ein kontinuierliches Spektrum zu zerlegen. Oft wird diese Transformation auch einfach als Fourier-Transformation bezeichnet.
Für eine Begriffsklärung, Interpretationen, Hintergrund- und Anwendungsinformationen sowie eine detaillierte mathematische Herleitung sei auf den Artikel zur Fourier-Transformation verwiesen. Hier soll nur kurz die Formel angegeben werden:
Für eine zu transformierende Funktion f(t) ist die kontinuierliche Fourier-Transformation definiert durch
die Rücktransformation (Fouriersynthese) lautet
Hierbei ist F(ω) das kontinuierliche Spektrum, das die Amplitude jeder Frequenz ω aus den reellen Zahlen angibt.
Wichtige Fourier-Transformations Paare
Hier eine Zusammenstellung wichtiger Fourier-Transformations-Paare. G und H sind die Fouriertransformierten der Funktionen g(t) bzw. h(t).
Signal Fouriertransformierte
KreisfrequenzFouriertransformierte
FrequenzHinweise 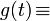
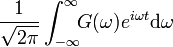

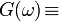
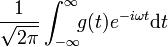
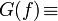
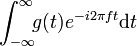
1 


Linearität 2 
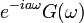
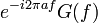
Zeitverschiebung 3 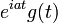
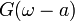
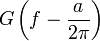
Frequenzverschiebung (Äquivalent zu Nr. 2) 4 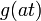


5 


Dualität der Fouriertransformation durch Vertauschung der Variablen 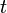 und
und  .
.6 

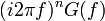
7 


Äquivalent zu Nr. 6 8 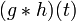
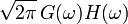
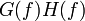
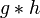 bedeutet die Faltung von
bedeutet die Faltung von  mit
mit 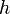
9 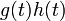
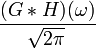
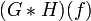
Äquivalent zu Nr. 8 Quadratisch integrierbare Funktionen Signal Fouriertransformierte
KreisfrequenzFouriertransformierte
FrequenzHinweise 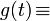
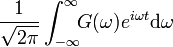

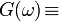
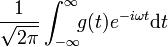
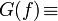
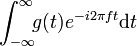
10 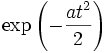
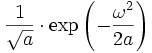
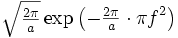
Die Gaußsche Funktion exp( − t2 / 2) ergibt fouriertransformiert wieder dieselbe Funktion. Für die Integrierbarkeit muss Re(a) > 0 sein. 11 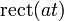
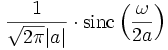

Die Rechteckfunktion und die sinc-Funktion. 12 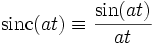
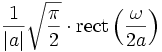
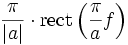
Äquivalent zu Nr. 11. Die Rechteckfunktion ist ein idealisierter Tiefpassfilter, und die sinc-Funktion ist die akausale Stoßantwort eines solchen Filters. 13 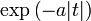

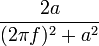
a > 0. Die FT der um den Ursprung exponentiell abfallenden Funktion ist eine Lorentzkurve. 14 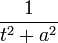
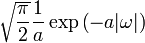
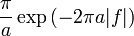
Äquivalent zu Nr. 13. Distributionen Signal Fouriertransformierte
KreisfrequenzFouriertransformierte
FrequenzHinweise 
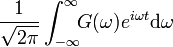

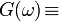
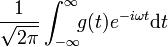
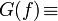
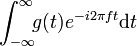
15 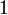


δ(ω) bezeichnet die Delta-Distribution. 16 
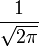
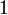
Äquivalent zu Nr. 15. 17 
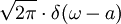
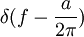
Folgt aus Nr. 3 und 15. 18 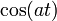
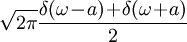
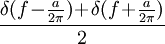
Folgt aus Nr. 1 und 17 19 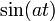

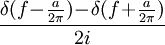
20 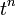
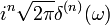

Hier ist n eine Natürliche Zahl. δn(ω) bezeichnet die n-te Ableitung der Delta-Distribution. 21 
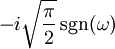

22 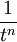
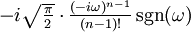
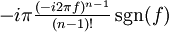
23 
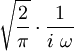
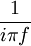
24 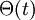
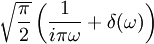
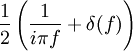
Θ(t) ist der Einheitssprung (Heaviside-Funktion). 25 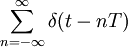

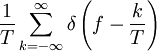
Beispiel
Als Beispiel soll das Frequenzspektrum einer gedämpften Schwingung mit ausreichend schwacher Dämpfung untersucht werden. Diese kann durch folgende Funktion beschrieben werden:
oder in komplexer Schreibweise:
Hier ist x0 die Amplitude und ωs die Kreisfrequenz der Schwingung, τ; die Zeit nach der die Amplitude auf 1 / e abgefallen ist und Θ(t) die Heaviside-Funktion. Das heißt, die Funktion ist nur für positive Zeiten nicht null.
Man erhält
Wikimedia Foundation.



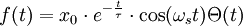





![= \frac{x_0}{2 \sqrt{2 \pi}} \left[ -{ 1 \over \frac{1}{\tau} -\mathrm{i}(\omega_s -\omega ) } e^{-t(\frac{1}{\tau} - \mathrm{i}(\omega_s - \omega))} - { 1 \over \frac{1}{\tau} +\mathrm{i}(\omega_s +\omega ) } e^{-t(\frac{1}{\tau} + \mathrm{i}(\omega_s + \omega))} \right]_0^\infty](/pictures/dewiki/49/16d4e66331e532667bf75367455d1ad4.png)

