Konvergenzpunkt — glausties taškas statusas T sritis fizika atitikmenys: angl. point of convergence vok. Konvergenzpunkt, m rus. точка сходимости, f pranc. point de convergence, m … Fizikos terminų žodynas
Konvergenzpunkt — Kon|ver|gẹnz|punkt 〈[ vɛr ] m. 1〉 Treffpunkt zweier sich gegenseitig nähernder Strahlen … Universal-Lexikon
Christliche Mystik — Der Ausdruck christliche Mystik ist ein Sammelbegriff für Texte, Autoren und Gruppierungen innerhalb des Christentums, auf welche rückblickend die religionswissensschaftliche Kategorie „Mystik“ anwendbar ist. Es werden allerdings unterschiedliche … Deutsch Wikipedia
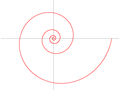
Cornu-Spirale — Form der Klothoide Die Klothoide, auch Klotoide (v. griechisch κλώθω „spinnen“), ist eine spezielle ebene Kurve. Andere Bezeichnungen für die Klothoide sind Cornu Spirale (nach Marie Alfred Cornu) und Spinnkurve (da der Graph, der von einem… … Deutsch Wikipedia
Cornuspirale — Form der Klothoide Die Klothoide, auch Klotoide (v. griechisch κλώθω „spinnen“), ist eine spezielle ebene Kurve. Andere Bezeichnungen für die Klothoide sind Cornu Spirale (nach Marie Alfred Cornu) und Spinnkurve (da der Graph, der von einem… … Deutsch Wikipedia
Eine gewisse Tendenz im französischen Film — (Originaltitel: Une certaine tendance du cinéma français) ist ein Artikel des damaligen Filmkritikers und späteren Filmregisseurs François Truffaut in der Filmzeitschrift Cahiers du cinéma aus dem Jahr 1954. Truffaut kritisierte darin das… … Deutsch Wikipedia
Einheitsklothoide — Form der Klothoide Die Klothoide, auch Klotoide (v. griechisch κλώθω „spinnen“), ist eine spezielle ebene Kurve. Andere Bezeichnungen für die Klothoide sind Cornu Spirale (nach Marie Alfred Cornu) und Spinnkurve (da der Graph, der von einem… … Deutsch Wikipedia
Einheitsklotoide — Form der Klothoide Die Klothoide, auch Klotoide (v. griechisch κλώθω „spinnen“), ist eine spezielle ebene Kurve. Andere Bezeichnungen für die Klothoide sind Cornu Spirale (nach Marie Alfred Cornu) und Spinnkurve (da der Graph, der von einem… … Deutsch Wikipedia
Fresnelsche Integrale — Form der Klothoide Die Klothoide, auch Klotoide (v. griechisch κλώθω „spinnen“), ist eine spezielle ebene Kurve. Andere Bezeichnungen für die Klothoide sind Cornu Spirale (nach Marie Alfred Cornu) und Spinnkurve (da der Graph, der von einem… … Deutsch Wikipedia
Fresnelsches Integral — Form der Klothoide Die Klothoide, auch Klotoide (v. griechisch κλώθω „spinnen“), ist eine spezielle ebene Kurve. Andere Bezeichnungen für die Klothoide sind Cornu Spirale (nach Marie Alfred Cornu) und Spinnkurve (da der Graph, der von einem… … Deutsch Wikipedia