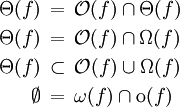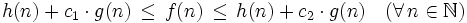- Kostenmaß
-
Landau-Symbole werden in der Mathematik und in der Informatik verwendet, um das asymptotische Verhalten von Funktionen und Folgen zu beschreiben. In der Informatik werden sie insbesondere in der Komplexitätstheorie verwendet, um verschiedene Probleme danach zu vergleichen, wie „schwierig“ oder aufwendig sie zu lösen sind.
Inhaltsverzeichnis
Geschichte
Der Großbuchstabe
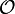 (damals eigentlich ein großes Omikron) als Symbol für Ordnung von wurde erstmals vom deutschen Zahlentheoretiker Paul Bachmann in der 1894 erschienenen zweiten Auflage seines Buchs Analytische Zahlentheorie verwendet. Bekannt gemacht wurde diese Notation durch den ebenfalls deutschen Zahlentheoretiker Edmund Landau, mit dessen Namen sie insbesondere im deutschen Sprachraum heute in Verbindung gebracht wird.[1]
(damals eigentlich ein großes Omikron) als Symbol für Ordnung von wurde erstmals vom deutschen Zahlentheoretiker Paul Bachmann in der 1894 erschienenen zweiten Auflage seines Buchs Analytische Zahlentheorie verwendet. Bekannt gemacht wurde diese Notation durch den ebenfalls deutschen Zahlentheoretiker Edmund Landau, mit dessen Namen sie insbesondere im deutschen Sprachraum heute in Verbindung gebracht wird.[1]Anschauliche Bedeutung
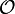 und o sind die am häufigsten verwendeten Landau-Symbole. Darüber hinaus gibt es noch Ω (Groß-Omega), ω (Klein-Omega) und Θ (Theta).
und o sind die am häufigsten verwendeten Landau-Symbole. Darüber hinaus gibt es noch Ω (Groß-Omega), ω (Klein-Omega) und Θ (Theta).Sie vergleichen das Wachstum von zwei Funktionen, meist im Unendlichen. In der nachfolgenden Tabelle ist f die Folge oder Funktion, über die eine Aussage getroffen werden soll, und g der einfachste Repräsentant einer Klasse gleich schnell wachsender Funktionen, die als Vergleich dienen.
Notation Anschauliche Bedeutung 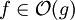
f wächst nicht wesentlich schneller als g 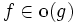
f wächst langsamer als g 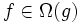
f wächst mindestens so schnell wie g 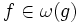
f wächst schneller als g 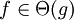
f wächst genauso schnell wie g Beispiele
In den folgenden Beispielen ist f stets als Funktion von x zu verstehen.
Notation Bedeutung Anschauliche Erklärung Beispiele für Laufzeiten 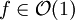
f ist beschränkt f überschreitet einen konstanten Wert nicht (unabhängig vom Wert des Arguments). Nachschlagen des i-ten Elementes in einem Array. 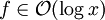
f logarithmisches Wachstum f wächst ungefähr um einen konstanten Betrag, wenn sich das Argument verdoppelt. Merke: Die Basis des Logarithmus ist egal.
Binäre Suche im sortierten Feld mit x Einträgen 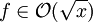
f Wachstum wie die Wurzelfunktion f wächst ungefähr auf das Doppelte, wenn sich das Argument vervierfacht 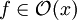
f lineares Wachstum f wächst ungefähr auf das Doppelte, wenn sich das Argument verdoppelt. Suche im unsortierten Feld mit x Einträgen 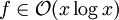
f super-lineares Wachstum Fortgeschrittenere Algorithmen zum Sortieren von x Zahlen 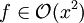
f quadratisches Wachstum f wächst ungefähr auf das Vierfache, wenn sich das Argument verdoppelt Einfache Algorithmen zum Sortieren von x Zahlen 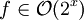
f exponentielles Wachstum f wächst ungefähr auf das Doppelte, wenn sich das Argument um eins erhöht Man kann hier jede Basis c > 1 verwenden, z.B e oder 10.
Rekursive Variante der Fibonacci-Folge 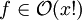
f faktorielles Wachstum f wächst ungefähr um das x-fache, wenn sich das Argument um eins von x − 1 auf x erhöht. Bogosort Formale Definition
In der folgenden Tabelle bezeichnen f und g entweder
- Folgen reeller Zahlen, dann ist
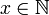 und der Grenzwert
und der Grenzwert 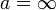 , oder
, oder - reellwertige Funktionen der reellen Zahlen, dann ist
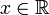 und der Grenzwert aus den erweiterten reellen Zahlen:
und der Grenzwert aus den erweiterten reellen Zahlen: 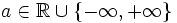 , oder
, oder - reellwertige Funktionen beliebiger topologischer Räume
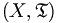 , dann ist
, dann ist  und auch der Grenzwert
und auch der Grenzwert 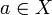 . Wichtigster Spezialfall ist dabei
. Wichtigster Spezialfall ist dabei 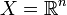 .
.
Formal lassen sich die Landau-Symbole dann mittels Limes superior und Limes inferior folgendermaßen definieren:
Notation Definition Mathematische Definition 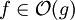
asymptotische obere Schranke 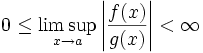
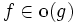
asymptotisch vernachlässigbar 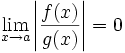
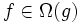
asymptotische untere Schranke, 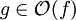
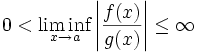
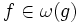
asymptotisch dominant, 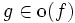
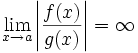
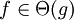
asymptotisch scharfe Schranke, sowohl 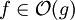 als auch
als auch 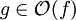
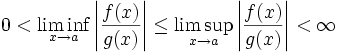
Definition mittels Quantoren
Äquivalent zur Definition mit Limessymbolen können für einen normierten Raum X, insbesondere also für die Fälle
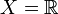 und
und 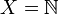 , folgende Definitionen mit Quantoren verwendet werden:
, folgende Definitionen mit Quantoren verwendet werden:Notation 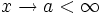
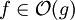
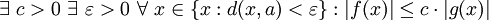
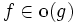
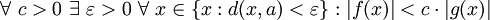
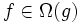
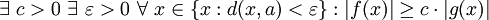
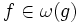
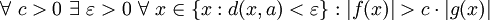
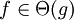
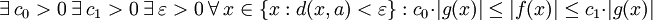
Notation 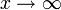
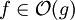
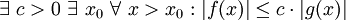
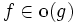
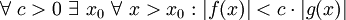
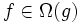
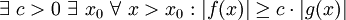
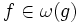
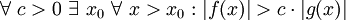
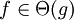
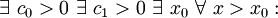
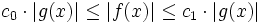
Analoge Definitionen lassen sich auch für den Fall
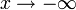 sowie für einseitige Grenzwerte geben.
sowie für einseitige Grenzwerte geben.Beispiele
Die Landau-Notation wird verwendet, um das asymptotische Verhalten bei Annäherung an einen endlichen oder unendlichen Grenzwert zu beschreiben. Das große O wird verwendet, um eine maximale Größenordnung anzugeben. So gilt beispielsweise nach der Stirling-Formel für das asymptotische Verhalten der Fakultät
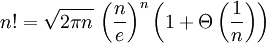 für
für 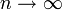
und
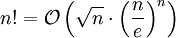 für
für 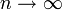 .
.
Der Faktor
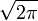 ist dabei nur eine Konstante und kann für die Abschätzung der Größenordnung vernachlässigt werden.
ist dabei nur eine Konstante und kann für die Abschätzung der Größenordnung vernachlässigt werden.Die Landau-Notation kann auch benutzt werden, um den Fehlerterm einer Approximation zu beschreiben. Beispielsweise besagt
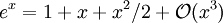 für
für 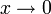 ,
,
dass der Absolutbetrag des Approximationsfehlers kleiner als eine Konstante mal x3 für x hinreichend nahe bei Null.
Das kleine o wird verwendet, um zu sagen, dass ein Ausdruck vernachlässigbar klein gegenüber dem angegebenen Ausdruck ist. Für differenzierbare Funktionen gilt beispielsweise
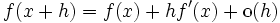 für
für 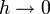 ,
,
der Fehler bei Approximation durch die Tangente geht also schneller als linear gegen 0.
Notationsfallen
Symbolisches Gleichheitszeichen
Oft wird in der Mathematik bei der Landau-Notation das Gleichheitszeichen verwendet. Es handelt sich dabei aber um eine rein symbolische Schreibweise und nicht um eine Gleichheitsaussage, auf die beispielsweise die Gesetze der Transitivität oder der Symmetrie anwendbar wären: In einer Aussage wie
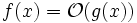 ist keine Seite der „Gleichung“ durch die andere bestimmt. Aus
ist keine Seite der „Gleichung“ durch die andere bestimmt. Aus 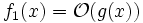 und
und 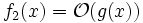 folgt nicht, dass f1 und f2 gleich sind. Genauso wenig kann man aus
folgt nicht, dass f1 und f2 gleich sind. Genauso wenig kann man aus 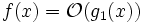 und
und 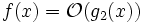 schließen, dass
schließen, dass 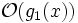 und
und 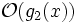 dieselbe Klasse sind oder die eine in der anderen enthalten ist.
dieselbe Klasse sind oder die eine in der anderen enthalten ist.Tatsächlich handelt es sich bei
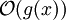 um eine Menge, welche alle diejenigen Funktionen enthält, welche höchstens so schnell wachsen wie g(x). Die Schreibweise
um eine Menge, welche alle diejenigen Funktionen enthält, welche höchstens so schnell wachsen wie g(x). Die Schreibweise 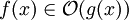 wäre also formal korrekt.
wäre also formal korrekt.Vergessener Grenzwert
Eine weitere Falle besteht darin, dass oft nicht angegeben wird, auf welchen Grenzwert sich das Landausymbol bezieht. Der Grenzwert ist aber wesentlich; so ist beispielsweise
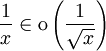 für
für 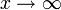 , nicht aber für den einseitigen Grenzwert
, nicht aber für den einseitigen Grenzwert 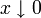 . Normalerweise wird der betrachtete Grenzwert aber aus dem Zusammenhang klar, sodass hier Mehrdeutigkeiten nur selten auftreten.
. Normalerweise wird der betrachtete Grenzwert aber aus dem Zusammenhang klar, sodass hier Mehrdeutigkeiten nur selten auftreten.Was beschreiben Ω, Ο und Θ?
Wie man aus der Definition erkennen kann, beschreiben Ω,
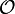 und Θ Mengen von Funktionen. Folgende Beziehungen zwischen diesen Funktionenmengen lassen sich aus der Definition ableiten:
und Θ Mengen von Funktionen. Folgende Beziehungen zwischen diesen Funktionenmengen lassen sich aus der Definition ableiten:Dennoch nutzt man die laxere Notation mit dem Gleichheitszeichen wie in
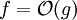 in der Praxis ausgiebig. Beispielsweise soll der Ausdruck f(n) = h(n) + Θ(g(n)) besagen, dass es Konstanten c1,c2 mit
in der Praxis ausgiebig. Beispielsweise soll der Ausdruck f(n) = h(n) + Θ(g(n)) besagen, dass es Konstanten c1,c2 mitgibt.
Anwendung in der Komplexitätstheorie
In der Komplexitätstheorie werden die Landau-Symbole vor allem angewendet, um den (minimalen oder maximalen) Bedarf an Speicher (Platzkomplexität) und Zeit (Zeitkomplexität) bezüglich eines bestimmten Maschinenmodells zu beschreiben.
Normalerweise ist es sehr aufwändig oder ganz unmöglich, für ein Problem L eine Funktion
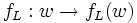 anzugeben, die allgemein jeder beliebigen Eingabe für ein Problem die zugehörige Anzahl der Rechenschritte (bzw. der Speicherzellen) zuordnet. Daher begnügt man sich in der Regel damit, statt jede Eingabe einzeln zu erfassen, sich lediglich auf die Eingabelänge n = | w | zu beschränken. Es ist aber meist ebenfalls zu aufwändig, eine Funktion
anzugeben, die allgemein jeder beliebigen Eingabe für ein Problem die zugehörige Anzahl der Rechenschritte (bzw. der Speicherzellen) zuordnet. Daher begnügt man sich in der Regel damit, statt jede Eingabe einzeln zu erfassen, sich lediglich auf die Eingabelänge n = | w | zu beschränken. Es ist aber meist ebenfalls zu aufwändig, eine Funktion 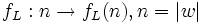 anzugeben.
anzugeben.Daher hat man die Landau-Notation entwickelt, die sich auf das asymptotische Verhalten der Funktion fL beschränkt. Man betrachtet also, in welchen Schranken sich der Rechenaufwand (der Bedarf an Speicher und Rechenzeit) hält, wenn man die Eingabe vergrößert. Das wichtigste Landau-Symbol ist
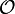 (großer lateinischer Buchstabe „O“), mit dem man obere Schranken angeben kann; untere Schranken sind im allgemeinen viel schwieriger zu finden. Dabei meint
(großer lateinischer Buchstabe „O“), mit dem man obere Schranken angeben kann; untere Schranken sind im allgemeinen viel schwieriger zu finden. Dabei meint 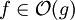 (oft auch
(oft auch 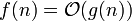 ), dass eine Konstante c > 0 und ein
), dass eine Konstante c > 0 und ein 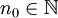 existieren, so dass für alle n > n0 gilt:
existieren, so dass für alle n > n0 gilt: 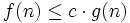 . In anderen Worten: Für alle Eingabelängen ist der Rechenaufwand f(n) nicht wesentlich größer – d. h. höchstens um einen konstanten Faktor c – als g(n).
. In anderen Worten: Für alle Eingabelängen ist der Rechenaufwand f(n) nicht wesentlich größer – d. h. höchstens um einen konstanten Faktor c – als g(n).Dabei ist die Funktion f nicht immer bekannt: Die Landau-Notation ist gerade dazu da, den Rechenaufwand (Platzbedarf) abzuschätzen, wenn es zu aufwändig ist, die genaue Funktion anzugeben, bzw. wenn diese zu kompliziert ist.
Die Landau-Symbole erlauben es dadurch, Probleme und Algorithmen nach ihrer Komplexität in Komplexitätsklassen zusammenzufassen.
In der Komplexitätstheorie lassen sich die verschiedenen Probleme und Algorithmen dann folgendermaßen vergleichen: Man kann für Problemstellungen mit Ω eine untere Schranke für beispielsweise die asymptotische Laufzeit angeben, mit
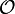 entsprechend eine obere Schranke. Bei
entsprechend eine obere Schranke. Bei 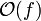 wird die Form von f (z. B. f(n) = n2) auch als die Komplexitätsklasse oder Aufwandsmaß bezeichnet (also z. B. quadratisch). Bei dieser Notation werden, wie die Definitionen der Landau-Symbole zeigen, konstante Faktoren vernachlässigt. Dies ist gerechtfertigt, da die Konstanten zu großen Teilen vom verwendeten Maschinenmodell bzw. bei implementierten Algorithmen von der Qualität des Compilers und diversen Eigenschaften der Hardware des ausführenden Computer abhängig sind. Damit können sie nicht direkt mit der Laufzeit des Algorithmus in Verbindung gebracht werden.
wird die Form von f (z. B. f(n) = n2) auch als die Komplexitätsklasse oder Aufwandsmaß bezeichnet (also z. B. quadratisch). Bei dieser Notation werden, wie die Definitionen der Landau-Symbole zeigen, konstante Faktoren vernachlässigt. Dies ist gerechtfertigt, da die Konstanten zu großen Teilen vom verwendeten Maschinenmodell bzw. bei implementierten Algorithmen von der Qualität des Compilers und diversen Eigenschaften der Hardware des ausführenden Computer abhängig sind. Damit können sie nicht direkt mit der Laufzeit des Algorithmus in Verbindung gebracht werden.Siehe auch: Grenzwert (Limes)
Quellen
- ↑ Earliest Uses of Symbols of Number Theory, 22. September 2006: According to Wladyslaw Narkiewicz in The Development of Prime Number Theory: “The symbols O(·) and o(·) are usually called the Landau symbols. This name is only partially correct, since it seems that the first of them appeared first in the second volume of P. Bachmann’s treatise on number theory (Bachmann, 1894). In any case Landau (1909a, p. 883) states that he had seen it for the first time in Bachmann's book. The symbol o(·) appears first in Landau (1909a).”
Weblinks
- Folgen reeller Zahlen, dann ist
Wikimedia Foundation.