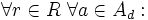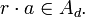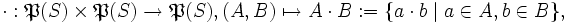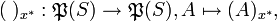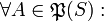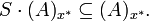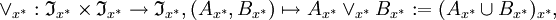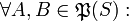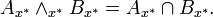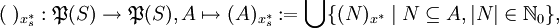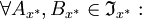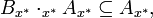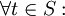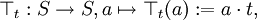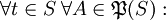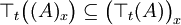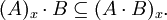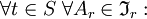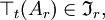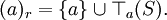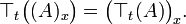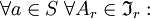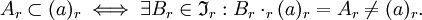Idealsystem

In der abstrakten Algebra ist ein Ideal eine Teilmenge einer algebraischen Struktur mit mindestens einer multiplikativen zweistelligen Operation, die abgeschlossen bezüglich Produkten mit Elementen aus der gesamten Struktur ist.

Die Ideale gleichen Typs auf einer gegebenen algebraischen Struktur bilden stets ein Hüllensystem, das Idealsystem genannt wird. Zu jedem Idealsystem ist immer ein entsprechender Hüllenoperator gegeben (und umgekehrt), das ist der zugehörige Idealoperator.

Zur einfacheren Darstellung wird hier nur der kommutative Fall beschrieben. Verzichtet man auf die Kommutativität der Multiplikation, dann handelt es sich im folgenden jedoch um Linksideale, und vertauscht man bei jedem Produkt den linken und den rechten Faktor, ergeben sich entsprechend Rechtsideale. Zweiseitige Ideale oder einfach nur Ideale sind sowohl Links- als auch Rechtsideale. Bei Kommutativität besteht kein Unterschied zwischen diesen drei Arten von Idealen.

„Klassische“ Ringideale

Zahlentheoretische Untersuchungen von Zahlenbereichen, bei denen eine eindeutige Primfaktorzerlegung von Elementen nicht mehr gegeben war, führten zur Entwicklung der „klassischen“ Idealtheorie für kommutative Ringe.

Definition

Ist 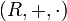$(R, +, \cdot)$ ein Ring, dann ist ein (dedekindsches) Ideal oder d-Ideal die Trägermenge 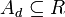$A_d \subseteq R$ einer Untergruppe von (R, + ), für die gilt:

$\forall r \in R \;\forall a \in A_d:$

$r \cdot a \in A_d.$

Eigenschaften

• Die Ideale eines Rings sind genau die Kerne der Ringhomomorphismen des Ringes.
• Die Ideale eines Rings bilden jeweils ein Hüllensystem, so dass die Ideale durch den zugehörigen Hüllenoperator 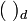$(\;)_d$ gegeben sind.

Bemerkungen

• Es entstanden weitere Idealbegriffe für Ringe, aber auch für andere algebraische Strukturen wie Verbände, Halbgruppen, Halbringe usw., die (mindestens) eine assoziative zweistellige Operation besitzen.
• Es gibt auch Ideale bei algebraischen Strukturen mit nicht assoziativen zweistelligen Operationen, z.B. Lie-Algebren.
• Der Begriff des Verbandsideals wurde auch für beliebige halbgeordnete Mengen zum Ordnungsideal verallgemeinert.
• In der Regel lässt man den Index weg, wenn klar ist, um welchen Hüllenoperator es sich handelt.

Allgemeine Idealoperatoren

Da in der Regel nur die jeweilige assoziative zweistellige Operation entscheidend für die Faktorisierung ist (der nicht assoziative Fall wird im folgenden nicht behandelt), ist es für eine allgemeine Idealtheorie ausreichend, Halbgruppen zu betrachten:

Gegeben sei im Folgenden stets eine kommutative multiplikative Halbgruppe 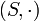$(S, \cdot)$, und es sei

$\cdot: \mathfrak P(S)\times\mathfrak P(S) \to \mathfrak P(S), (A, B) \mapsto A \cdot B := \{a\cdot b \mid a \in A, b \in B\},$

die Komplexmultiplikation über 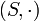$(S, \cdot)$, wobei 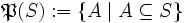$\mathfrak P(S) := \{A \mid A \subseteq S\}$ die Potenzmenge von S ist.

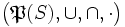$\bigl(\mathfrak P(S), \cup, \cap, \cdot\bigr)$ bildet dann einen u.a. kommutativen, assoziativen, vollständigen multiplikativen Verband mit einem Nullelement $\emptyset$.

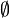Definition

Es soll nun

$(\;)_{x^*}: \mathfrak P(S) \to \mathfrak P(S), A \mapsto (A)_{x^*},$

ein Hüllenoperator auf S sein, mit der Eigenschaft, dass

$\forall A \in \mathfrak P(S):$

$S \cdot (A)_{x^*} \subseteq (A)_{x^*}.$

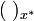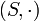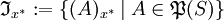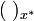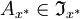$(\;)_{x^*}$ wird dann ein x ^* -Idealoperator oder kurz x ^* -Operator auf $(S, \cdot)$ genannt, $\mathfrak I_{x^*} := \{(A)_{x^*} \mid A \in \mathfrak P(S)\}$ ist das x ^* -Idealsystem bzw. x ^* -System zu $(\;)_{x^*}$, ein $A_{x^*} \in \mathfrak I_{x^*}$ heißt x ^* -Ideal und 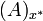$(A)_{x^*}$ ist das von 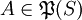$A \in \mathfrak P(S)$ erzeugte x ^* -Ideal. 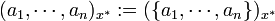$(a_1, \cdots, a_n)_{x^*} := (\{a_1, \cdots, a_n\})_{x^*}$ bezeichnet das von 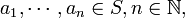$a_1, \cdots, a_n \in S, n \in \Bbb N,$ erzeugte x ^* -Ideal und 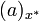$(a)_{x^*}$ ist das von 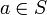$a \in S$ erzeugte x ^* -Hauptideal.

Bemerkung

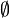• $\emptyset$ ist gewöhnlich kein Ideal, weil es aber für die Idealarithmetik von Vorteil ist, soll hier auch 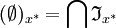$(\emptyset)_{x^*} = \bigcap\mathfrak I_{x^*}$ ein unechtes x ^* -Hauptideal sein, falls $(\emptyset)_{x^*} = \emptyset$.

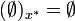Idealverbände

Auf 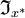$\mathfrak I_{x^*}$ sind zwei zweistellige Operationen

$\vee_{x^*}: \mathfrak I_{x^*}\times\mathfrak I_{x^*} \to \mathfrak I_{x^*}, (A_{x^*}, B_{x^*}) \mapsto A_{x^*} \vee_{x^*} B_{x^*} := (A_{x^*} \cup B_{x^*})_{x^*},$

$\wedge_{x^*}: \mathfrak I_{x^*}\times\mathfrak I_{x^*} \to \mathfrak I_{x^*}, (A_{x^*}, B_{x^*}) \mapsto A_{x^*} \wedge_{x^*} B_{x^*} := (A_{x^*} \cap B_{x^*})_{x^*},$

gegeben, so dass 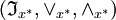$(\mathfrak I_{x^*}, \vee_{x^*}, \wedge_{x^*})$ einen vollständigen Verband bildet, den Verband der x ^* -Ideale von 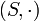$(S, \cdot)$. Dabei ist 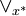$\vee_{x^*}$ die x ^* -Idealverbindung, 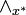$\wedge_{x^*}$ der x ^* -Idealdurchschnitt.

Wie für alle Hüllensysteme gilt auch für jedes x ^* -Idealsystem:

$\forall A, B \in \mathfrak P(S):$

$A_{x^*} \wedge_{x^*} B_{x^*} = A_{x^*} \cap B_{x^*}.$

Algebraische Idealoperatoren

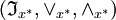$(\mathfrak I_{x^*}, \vee_{x^*}, \wedge_{x^*})$ ist genau dann algebraisch, wenn 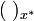$(\;)_{x^*}$ algebraisch ist, also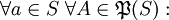

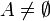$\forall a \in S \;\forall A \in \mathfrak P(S):$

$A \neq \emptyset$ und $a \in (A)_{x^*} \implies \exists a_1, \cdots, a_n \in A; n \in \Bbb N: a \in (a_1, \cdots, a_n)_{x^*}.$

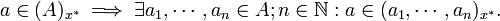
Bezeichnet | A | die Mächtigkeit der Menge A, so existiert mit

$(\;)_{x^*_s}: \mathfrak P(S) \to \mathfrak P(S), A \mapsto (A)_{x^*_s} := \bigcup \{(N)_{x^*} \mid N \subseteq A, |N| \in \Bbb N_0\},$

immer ein algebraischer x ^* -Idealoperator zu $(\;)_{x^*}$.

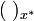x-Idealoperatoren

Die x ^* -Idealmultiplikation

$\cdot_{x^*}: \mathfrak I_{x^*}\times\mathfrak I_{x^*} \to \mathfrak I_{x^*}, (A_{x^*}, B_{x^*}) \mapsto A_{x^*} \cdot_{x^*} B_{x^*} := (A_{x^*} \cdot B_{x^*})_{x^*},$

besitzt zwar die für Ideale charakteristische Eigenschaft

$\forall A_{x^*}, B_{x^*} \in \mathfrak I_{x^*}:$

$B_{x^*} \cdot_{x^*} A_{x^*} \subseteq A_{x^*},$

sie bietet aber im Allgemeinen noch nicht genügend Eigenschaften, um 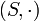$(S, \cdot)$ gut untersuchen zu können. Als gut geeignet für eine allgemeine Idealtheorie hat sich hingegen die folgende Klasse von x ^* -Idealoperatoren erwiesen.

Definition

So genannte x-Idealoperatoren bzw. x-Operatoren 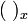$(\;)_x$ sind x ^* -Idealoperatoren, bei denen Translationen

$\forall t \in S:$

$\top_{t}: S \to S, a \mapsto \top_{t}(a) := a \cdot t,$

``stetig´´ sind wie bei topologischen Abschlussoperatoren:

$\forall t \in S \;\forall A \in \mathfrak P(S):$

$\top_{t}\bigl((A)_x\bigr) \subseteq \bigl(\top_{t}(A)\bigr)_x$

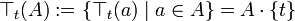mit $\top_{t}(A) := \{\top_{t}(a) \mid a \in A\} = A \cdot \{t\}$ für jedes 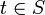$t \in S$ und alle $A \in \mathfrak P(S)$.

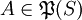Eigenschaften

• Mit jedem x-Idealoperator 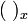$(\;)_x$ ist auch 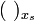$(\;)_{x_s}$ ein x-Idealoperator.
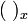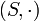• Für jeden x-Idealoperator $(\;)_x$ auf $(S, \cdot)$ folgt sogar

$\forall A, B \in \mathfrak P(S):$

$(A)_x \cdot B \subseteq (A \cdot B)_x.$

• Die zweiseitigen x-Ideale einer Halbgruppe 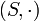$(S, \cdot)$ sind genau die Kerne von bestimmten Halbgruppenhomomorphismen von 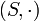$(S, \cdot)$, und es gilt

$\forall A, B \in \mathfrak P(S):$

$(A)_x \cdot_x (B)_x = (A \cdot B)_x.$

• Ein zweiseitiges x-Idealsystem bildet einen (kommutativen,) assoziativen, quasiganzen und vollständigen multiplikativen Verband $(\mathfrak I_x, \vee_x, \wedge_x, \cdot_x)$.
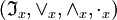• Ebenso ist 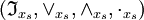$(\mathfrak I_{x_s}, \vee_{x_s}, \wedge_{x_s}, \cdot_{x_s})$ für zweiseitige x-Ideale ein solcher multiplikativer Verband, der zudem stets algebraisch ist.

Bemerkungen

• Ein beliebiger x ^* -Idealoperator induziert stets einen x-Idealoperator, so dass auch x-Idealoperatoren sehr allgemeiner Natur sind.
• Ein anderer, abstrakter Ansatz für eine allgemeine Idealtheorie ist die Beschreibung von Idealsystemen durch entsprechende multiplikative Verbände.
• In der Regel können Begriffe aus der ``klassischen´´ Idealtheorie, wie Maximalideal, Primideal usw., problemlos für x-Ideale übernommen werden.

r-Idealoperatoren

Definition

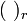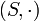Ein r-Idealoperator $(\;)_r$ auf $(S, \cdot)$ ist ein x-Idealoperator, der zusätzlich translationsabgeschlossenen ist, also

$\forall t \in S \;\forall A_r \in \mathfrak I_r:$

$\top_{t}(A_r) \in \mathfrak I_r,$

und für den auch noch gilt:

$\forall a \in S:$

$(a)_r = \{a\} \cup \top_{a}(S).$

Eigenschaften

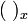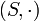• Für jeden translationsabgeschlossenen x-Idealoperator $(\;)_x$ auf $(S, \cdot)$ folgt sogar

$\forall t \in S \;\forall A \in \mathfrak P(S):$

$\top_{t}\bigl((A)_x\bigr) = \bigl(\top_{t}(A)\bigr)_x.$

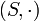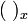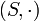• Besitzt $(S, \cdot)$ ein Einselement 1, dann ist jeder translationsabgeschlossene x-Idealoperator $(\;)_x$ auf $(S, \cdot)$ bereits ein r-Idealoperator und

$\forall a \in S:$

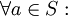
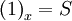$\left(1\right)_x = S$ und $(a)_x = \top_{a}(S) = S \cdot \{a\}.$

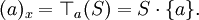
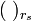• $(\;)_{r_s}$ ist ebenfalls ein r-Idealoperator.
• Jedes zweiseitige r-Hauptideal ist ein Multiplikationsideal, d.h.

$\forall a \in S \;\forall A_r \in \mathfrak I_r:$

$A_r \subset (a)_r \iff \exists B_r \in \mathfrak I_r: B_r \cdot_r (a)_r = A_r \neq (a)_r.$

• Ein zweiseitiges (a)_r ist in 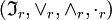$(\mathfrak I_r, \vee_r, \wedge_r, \cdot_r)$ kürzbar, also

$\forall a \in S \;\forall A_r, B_r \in \mathfrak I_r:$

$A_r \cdot_r (a)_r = B_r \cdot_r (a)_r \implies A_r = B_r,$

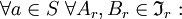
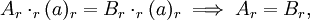
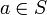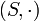wenn $a \in S$ in $(S, \cdot)$ kürzbar ist.

Bemerkung

• r-Idealsysteme weisen alle wesentlichen Eigenschaften der d-Idealsysteme von Ringen auf, weshalb sie eine gute Untersuchung der Teilbarkeitsverhältnisse in 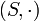$(S, \cdot)$ erlauben.

Literatur

• H. Prüfer: Untersuchungen über die Teilbarkeitseigenschaften von Körpern. J. reine angew. Math. 168 (1932), 1--36.
• K. E. Aubert: Theory of x-ideals. Acta Math. 107 (1962), 1--52.
• I. Fleischer: Equivalence of x-systems and m-lattices, in: Colloquia Mathematica Societatis Janos Bolyai, 33. Contributions to Lattice Theory, Szeged, 1980. North-Holland, Amsterdam-Oxford-New York, 1983, S. 381--400.
• P. Lorenzen: Abstrakte Begründung der multiplikativen Idealtheorie. Math. Z. 45 (1939), 533--553.
• M. Ward, R.P. Dilworth: The lattice theory of ova. Ann. Math. 40 (1939), 600--608.
• L. Fuchs: Teilweise geordnete algebraische Strukturen. Vandenhoeck & Ruprecht, Göttingen, 1966.
• G. Birkhoff: Lattice Theory. American Mathematical Society, Providence, R.I., 3rd ed. 1973.