- L'Hospitalsche Regel
-
Mit der Regel von L’Hospital (gesprochen [lopi'tal], auch L’Hôpital geschrieben) lassen sich Grenzwerte von Funktionen, die sich als Quotient zweier gegen 0 konvergierender oder bestimmt divergierender Funktionen schreiben lassen, mit Hilfe der ersten Ableitungen dieser Funktionen berechnen.
Die Regel ist nach Guillaume François Antoine, Marquis de L’Hospital (1661–1704) benannt. L’Hospital veröffentlichte sie 1696 in seinem Buch Analyse des infiniment petits pour l’intelligence des lignes courbes, dem ersten Lehrbuch der Differentialrechnung. Er hatte sie aber nicht selbst entdeckt, sondern von Johann Bernoulli übernommen.
Inhaltsverzeichnis
Anwendung
Die Regel von L’Hospital erlaubt es in vielen Fällen, den Grenzwert einer Funktion zu bestimmen, wenn sich der Funktionsterm so ausdrücken lässt, dass beim Erreichen der Grenze ein unbestimmter Ausdruck entsteht.
Alle Anwendungen der Regel lassen sich auf die Aufgabe zurückführen, den Grenzwert
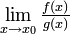 zu bestimmen, wenn sowohl
zu bestimmen, wenn sowohl 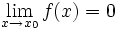 als auch
als auch 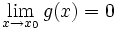 gilt,
gilt, 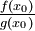 ist also ein unbestimmter Ausdruck des Typs
ist also ein unbestimmter Ausdruck des Typs 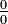 .
.Die Regel von L’Hospital besagt dann, dass
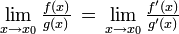 gilt, falls der Grenzwert auf der rechten Seite existiert. f' und g' bezeichnen dabei die ersten Ableitungen der Funktionen f und g.
gilt, falls der Grenzwert auf der rechten Seite existiert. f' und g' bezeichnen dabei die ersten Ableitungen der Funktionen f und g.Die rechte Seite dieser Gleichung lässt sich häufig einfach berechnen. Führt auch sie wieder auf einen unbestimmten Ausdruck, so kann man darauf erneut die Regel von L’Hospital anwenden, was möglicherweise in endlich vielen Schritten zum Ziel führt. Starres Festhalten an der Regel von L’Hospital kann aber auch zu längeren und schwierigeren Rechnungen führen.
Die Umkehrung der Regel gilt nicht: Daraus, dass der Grenzwert
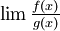 existiert, folgt nicht zwingend, dass auch
existiert, folgt nicht zwingend, dass auch 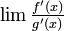 existiert.
existiert.Präzise Formulierung
Sei I = ]a,b[ ein nichtleeres offenes Intervall und seien
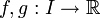 differenzierbare Funktionen, die für
differenzierbare Funktionen, die für 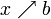 (x geht von unten gegen b) beide gegen 0 konvergieren oder beide bestimmt divergieren. Wenn
(x geht von unten gegen b) beide gegen 0 konvergieren oder beide bestimmt divergieren. Wenn 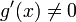 für alle
für alle 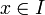 gilt sowie
gilt sowie 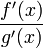 für
für 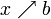 gegen einen Wert c konvergiert oder bestimmt divergiert, so tut dies auch
gegen einen Wert c konvergiert oder bestimmt divergiert, so tut dies auch 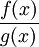 . Analoges gilt, wenn man
. Analoges gilt, wenn man 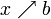 überall durch
überall durch 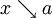 (x geht von oben gegen a) ersetzt.
(x geht von oben gegen a) ersetzt.Anschauliche Erklärung
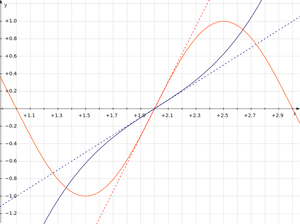
Die Regel beruht darauf, dass sich Funktionen in der Nähe einer Stelle x0 durch ihre Tangenten annähern lassen.
Ist
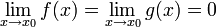 , so lauten die Tangentengleichungen
, so lauten die Tangentengleichungen 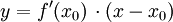 und
und 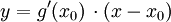 . Ihr Quotient
. Ihr Quotient 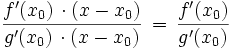 ist also eine Näherung für
ist also eine Näherung für 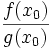 .
.Anwendungsbeispiele
Grenzübergang bei 0
Zu untersuchen ist die Konvergenz bzw. Divergenz von
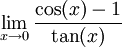 . Dazu setzt man
. Dazu setzt man 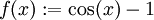 und
und 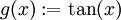 . Es gilt
. Es gilt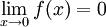 und
und 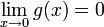 .
.
Falls
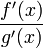 für
für 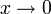 konvergiert oder bestimmt divergiert, darf die Regel von L’Hospital angewandt werden. Nun gilt
konvergiert oder bestimmt divergiert, darf die Regel von L’Hospital angewandt werden. Nun gilt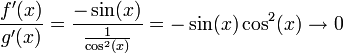 für
für 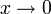 .
.
Somit ist die Regel von L’Hospital anwendbar. Mit dieser folgt die Konvergenz von
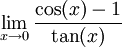 mit Grenzwert 0.
mit Grenzwert 0.Grenzübergang im Unendlichen
Zu untersuchen ist die Konvergenz bzw. Divergenz von
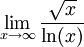 . Man setzt
. Man setzt 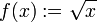 und
und 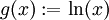 . Sowohl
. Sowohl 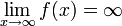 als auch
als auch 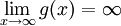 ist bestimmt divergent.
ist bestimmt divergent.Falls
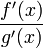 für
für 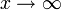 konvergiert oder bestimmt divergiert, dürfte die Regel von L’Hospital angewandt werden. Nun gilt
konvergiert oder bestimmt divergiert, dürfte die Regel von L’Hospital angewandt werden. Nun gilt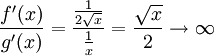 für
für 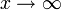 ,
,
d. h.,
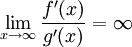 ist bestimmt divergent. Daher darf die Regel von L’Hospital angewandt werden. Aus ihr folgt die bestimmte Divergenz
ist bestimmt divergent. Daher darf die Regel von L’Hospital angewandt werden. Aus ihr folgt die bestimmte Divergenz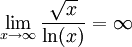 .
.
Warnbeispiele
Beachtung der Voraussetzungen
Sei
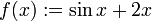 und
und 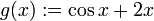 . Für
. Für 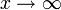 liegt der Fall
liegt der Fall 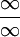 vor.
vor.Die Regel von L’Hospital kann aber nicht angewandt werden, denn
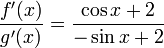 ist für
ist für 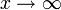 unbestimmt divergent, da eine periodische Funktion vorliegt. Trotz des Versagens der Regel von L’Hospital konvergiert
unbestimmt divergent, da eine periodische Funktion vorliegt. Trotz des Versagens der Regel von L’Hospital konvergiert 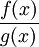 für
für 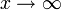 . Es ist nämlich
. Es ist nämlich 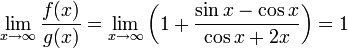 .
.Landau-Kalkül
Wenn man den Grenzwert
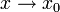 berechnen möchte und die Taylorentwicklung von Nenner und Zähler um x0 kennt, ist es oft einfacher, den Grenzwert über den -Kalkül zu bestimmen, als mehrfach die Regel von L’Hospital anzuwenden.
berechnen möchte und die Taylorentwicklung von Nenner und Zähler um x0 kennt, ist es oft einfacher, den Grenzwert über den -Kalkül zu bestimmen, als mehrfach die Regel von L’Hospital anzuwenden.So gilt beispielsweise
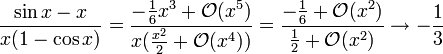 für
für 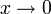 .
.Literatur
- Harro Heuser: Lehrbuch der Analysis. Teil 1. 12. Auflage. Teubner, Stuttgart/Leipzig, 1998.
Weblinks
Wikimedia Foundation.