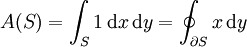Satz von Green — Der Satz von Green (auch Green Riemannsche Formel oder Lemma von Green, gelegentlich auch Satz von Gauß Green) erlaubt es, das Integral über eine ebene Fläche durch ein Kurvenintegral auszudrücken. Der Satz ist ein Spezialfall des Satzes von… … Deutsch Wikipedia
Liste der Namensvarianten von Jazzmusikern — Hinweise zur Nutzung der Tabelle Diese Listen sind sortierbar. Die Voreinstellung erfolgt nach dem Nachnamen der Musiker (Lemma). Darüber hinaus kann sie nach dem Spitznamen bzw. dem islamischen, indischen oder afrikanischen Namen der Künstler,… … Deutsch Wikipedia
Liste mathematischer Sätze — Inhaltsverzeichnis A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A Satz von Abel Ruffini: eine allgemeine Polynomgleichung vom … Deutsch Wikipedia
Finite-Elemente-Analyse — Die Finite Elemente Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung, insbesondere elliptischer partieller Differentialgleichungen mit Randbedingungen. Sie ist auch ein weit verbreitetes modernes Berechnungsverfahren im… … Deutsch Wikipedia
Finite-Elemente-Verfahren — Die Finite Elemente Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung, insbesondere elliptischer partieller Differentialgleichungen mit Randbedingungen. Sie ist auch ein weit verbreitetes modernes Berechnungsverfahren im… … Deutsch Wikipedia
Finite Elemente — Die Finite Elemente Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung, insbesondere elliptischer partieller Differentialgleichungen mit Randbedingungen. Sie ist auch ein weit verbreitetes modernes Berechnungsverfahren im… … Deutsch Wikipedia
Finite Elementemethode — Die Finite Elemente Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung, insbesondere elliptischer partieller Differentialgleichungen mit Randbedingungen. Sie ist auch ein weit verbreitetes modernes Berechnungsverfahren im… … Deutsch Wikipedia
Methode der finiten Elemente — Die Finite Elemente Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung, insbesondere elliptischer partieller Differentialgleichungen mit Randbedingungen. Sie ist auch ein weit verbreitetes modernes Berechnungsverfahren im… … Deutsch Wikipedia
Issai Schur — Issai Schur[1] (* 10. Januar 1875 in Mogiljow; † 10. Januar 1941 in Tel Aviv) war ein Mathematiker, der die meiste Zeit seines Lebens in Deutschland arbeitete. Als Student von Frobenius arbeitete er über Darstellungstheorie von Gruppen, aber auch … Deutsch Wikipedia
Regular semigroup — A regular semigroup is a semigroup S in which every element is regular, i.e., for each element a , there exists an element x such that axa = a . [Howie 1995 : 54.] Regular semigroups are one of the most studied classes of semigroups, and their… … Wikipedia
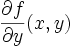 und
und 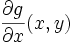 ebenfalls stetig auf S. Dann gilt
ebenfalls stetig auf S. Dann gilt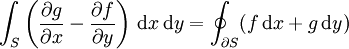 .
.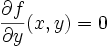 und
und 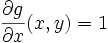 kann der Flächeninhalt eines Gebietes alleine durch den Verlauf der Randkurve bestimmt werden:
kann der Flächeninhalt eines Gebietes alleine durch den Verlauf der Randkurve bestimmt werden: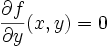 und
und 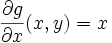 bzw.
bzw. 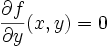 und
und 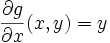 die Momente erster Ordnung durch ein Kurvenintegral berechnet werden, um den Schwerpunkt der Fläche S zu bestimmen:
die Momente erster Ordnung durch ein Kurvenintegral berechnet werden, um den Schwerpunkt der Fläche S zu bestimmen: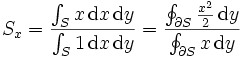 .
.