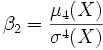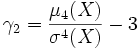leptokurtisch — hochgipflig … Universal-Lexikon
hochgipflig — leptokurtisch * * * ∙hoch|gipf|lig <Adj.> [zu Gipfel in der landsch. Bed. „oberer (rundlicher) Teil von etw.“]: (schweiz.) stark nach oben gewölbt; mit einer hervortretenden Verzierung versehen: hatte ... viele e Metallknöpfe auf der Weste… … Universal-Lexikon
Exzess (Statistik) — Die Wölbung (auch Kurtosis oder Exzess) einer statistischen Verteilung X ist definiert als normierte Form des vierten zentralen Moments μ4(X). Sie beschreibt die „Spitzigkeit“ der Wahrscheinlichkeitsdichtefunktion. Die Wölbung gibt es in… … Deutsch Wikipedia
Flachgipflig — Die Wölbung (auch Kurtosis oder Exzess) einer statistischen Verteilung X ist definiert als normierte Form des vierten zentralen Moments μ4(X). Sie beschreibt die „Spitzigkeit“ der Wahrscheinlichkeitsdichtefunktion. Die Wölbung gibt es in… … Deutsch Wikipedia
Kurtosis — Die Wölbung (auch Kurtosis oder Exzess) einer statistischen Verteilung X ist definiert als normierte Form des vierten zentralen Moments μ4(X). Sie beschreibt die „Spitzigkeit“ der Wahrscheinlichkeitsdichtefunktion. Die Wölbung gibt es in… … Deutsch Wikipedia
Mesokurtisch — Die Wölbung (auch Kurtosis oder Exzess) einer statistischen Verteilung X ist definiert als normierte Form des vierten zentralen Moments μ4(X). Sie beschreibt die „Spitzigkeit“ der Wahrscheinlichkeitsdichtefunktion. Die Wölbung gibt es in… … Deutsch Wikipedia
Platykurtisch — Die Wölbung (auch Kurtosis oder Exzess) einer statistischen Verteilung X ist definiert als normierte Form des vierten zentralen Moments μ4(X). Sie beschreibt die „Spitzigkeit“ der Wahrscheinlichkeitsdichtefunktion. Die Wölbung gibt es in… … Deutsch Wikipedia
Steilgipflig — Die Wölbung (auch Kurtosis oder Exzess) einer statistischen Verteilung X ist definiert als normierte Form des vierten zentralen Moments μ4(X). Sie beschreibt die „Spitzigkeit“ der Wahrscheinlichkeitsdichtefunktion. Die Wölbung gibt es in… … Deutsch Wikipedia
Volax-Future — Ein Volax Future ist ein Finanzterminkontrakt auf die implizite Volatilität einer DAX Option am Geld mit drei Monaten Restlaufzeit. 1998 wurde der Volax Future als erster Terminkontrakt auf implizite Optionsvolatilitäten an der DTB (heute Eurex)… … Deutsch Wikipedia
Wölbung (Statistik) — Die Wölbung oder Kurtosis (griechisch κύρτωσης kyrtōsis‚ das Krümmen, Wölben) ist eine Maßzahl für die Steilheit bzw. „Spitzigkeit“ einer (eingipfligen) Wahrscheinlichkeitsfunktion, statistischen Dichtefunktion oder Häufigkeitsverteilung.[1] … Deutsch Wikipedia