Volax-Future

Ein Volax-Future ist ein Finanzterminkontrakt auf die implizite Volatilität einer DAX-Option am Geld mit drei Monaten Restlaufzeit. 1998 wurde der Volax-Future als erster Terminkontrakt auf implizite Optionsvolatilitäten an der DTB (heute Eurex) eingeführt. Nach ca. 15.000 gehandelten Kontrakten wurde der Handel mit dem Volax-Future allerdings Ende 1998 aufgrund stark gesunkener Liquidität wieder eingestellt.

Seit der Veröffentlichung des Black-Scholes-Modells (1973) ist der enorme Einfluss des Faktors Volatilität auf den Optionspreis bekannt. Im Gegensatz zu anderen Optionspreisfaktoren, wie dem Kurs des Underlyings und dem Zins, ließ sich die Volatilität bis 1998 nicht separat mit einem einzigen Finanzinstrument handeln. Im Folgenden wird gezeigt, wie der Volax-Future auf die impliziten Volatilitäten der DAX-Option ausgestaltet war und welche Anwendungsbereiche es für Volatilitätsfuture wie den Volax-Future gibt.

1973 war in mehrfacher Hinsicht ein bemerkenswertes Jahr für die internationalen Terminbörsen. Zum einen sorgte der Zusammenbruch des Bretton Woods Systems fester Wechselkurse für signifikant höhere Volatilitäten auf den Zins- und Devisenmärkten und in der Konsequenz für einen bis heute ungebrochenen Aufschwung der derivativen Instrumente in diesen Bereichen. Zum anderen führte die CBOE in Chicago als erste Terminbörse der Welt Optionen auf Aktien ein. Dies wurde erst durch die Ergebnisse von Fischer Black und Myron Scholes ermöglicht, die gemeinsam ein Optionspreismodell zur Bewertung von Aktienoptionen europäischer Art veröffentlichten. Obwohl die Herleitung der Optionspreisformel im Original sehr aufwändig ist und das Modell nur unter idealtypischen Prämissen gilt, setzte sich das Modell in der Praxis schnell durch. Noch heute ist es das am weitesten verbreitete Optionspreismodell. Denn zum einen liegt der rechnerische Optionspreis P des Black-Scholes-Modells in der Regel sehr nahe an dem Preis, zu dem die jeweilige Option tatsächlich gehandelt wird. Zum anderen benötigt das Modell nur fünf Inputfaktoren, nämlich den aktuellen Aktienkurs S, den Ausübungspreis E, die Restlaufzeit t der Option, den risikolosen Zinssatz r sowie die Standardabweichung σ der Aktienrendite. Der letztgenannte Faktor wird auch als Volatilität bezeichnet.

Der Wert eines Portfolios mit Optionen schwankt in Abhängigkeit von Änderungen der Volatilität. Zur Absicherung dieses Volatilitätsrisikos gibt es derzeit keine reinen Hedginginstrumente. Der vorliegende Aufsatz zeigt am Beispiel des Volax-Futures auf die implizite Volatilität von DAX-Optionen, wie ein Future auf implizite Volatilitäten aussehen kann. Dazu werden zunächst die impliziten Volatilität definiert und einige ihrer Eigenschaften dargestellt. Anschließend wird ein Futureskurs für Volatilitäten hergeleitet und die konkrete Ausgestaltung des Volatilitätsfutures beschrieben. Darauf aufbauend werden die Anwendungsbereiche Hedging, Spekulation und Arbitrage eines solchen Derivates erklärt.

Merkmale impliziter Volatilität

Definition

Sind der Preis einer Option sowie die preisbeeinflussenden Faktoren Laufzeit, Kurs des Underlyings, Zinsen und Basispreis bekannt, so lässt sich mittels eines Optionspreismodells die noch fehlende Größe Volatilität bestimmen. Die auf diese Art bestimmte Volatilität wird implizite Volatilität genannt. Die Formel des Black/Scholes-Modells sowie der anderen gängigen Optionspreismodelle lässt sich nicht nach der Volatilität σ umstellen. Daher müssen zur Bestimmung der impliziten Volatilität numerische Näherungsverfahren verwendet werden. Bei europäischen Standardoptionen, wie sie im Black-Scholes-Modell unterstellt werden, bietet sich dazu das Newton-Raphson-Verfahren an. Es ist sehr effizient und konvergiert in der Regel innerhalb von drei oder vier Iterationen zu der gesuchten impliziten Volatilität.

Volatilitätssmile

Black/Scholes unterstellen in ihrem Modell unabhängig vom Basispreis und der Laufzeit der Option konstante Volatilitäten. Demnach müssten die impliziten Volatilitäten einer Option bei unterschiedlichen Basispreisen und verschieden langen Laufzeiten immer gleich sein. Dies ist jedoch nicht der Fall. Grafik 1

1-Volatilitätssmile

zeigt die impliziten Volatilitäten von DAX-Call-Optionen mit unterschiedlichen Basispreisen bei gleicher Restlaufzeit.

Auffallend ist der konvexe Verlauf der impliziten Volatilitäten. Je weiter der Basispreis unter dem aktuellen DAX-Kurs liegt, desto höher ist die implizite Volatilität. Hauptursache dafür ist, dass die DAX-Renditen entgegen den Annahmen im Black-Scholes-Modell nicht normalverteilt sind. Die Tabelle zeigt, dass die DAX-Renditen zwischen dem 2. Januar 1987 und dem 9. April 1997 leptokurtisch verteilt waren.

Kennzahlen der täglichen DAX-Renditen zwischen 2. Januar 1987 und 9. April 1997

Mittelwert	0,000412
Standardabweichung	0,012147
Schiefe	-0,801822
Kurtosis	12,342076

Dies bedeutet, es existieren gegenüber der Normalverteilungsannahme höhere Wahrscheinlichkeiten, dass sich die DAX-Renditen entweder nicht verändern oder aber extreme Abweichungen von ihrem Mittelwert aufweisen. Crash-Situationen sind im DAX wahrscheinlicher als extreme Kurssteigerungen. Weitere mögliche Gründe für die Volatilitätssmiles ergeben sich aus den Geld/Brief-Spannen bei besonders weit aus dem Geld liegenden Optionen sowie der generell niedrigeren Liquidität von nicht am Geld befindlichen Optionen. Die Existenz der Volatilitätssmiles hat, wie noch zu zeigen ist, einen nicht unerheblichen Einfluss auf die Gestaltung eines Volatilitätsfutures.

Zeitstruktur der Volatilität

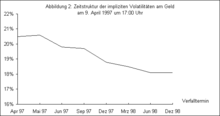
Grafik 2

2-Zeitstruktur der Volatilität

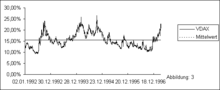
zeigt die impliziten Volatilitäten am Geld befindlicher DAX-Calls mit unterschiedlichen Restlaufzeiten. Entgegen den Annahmen des Black/Scholes-Modells weisen verschiedene Laufzeiten nicht identische implizite Volatilitäten auf. Dies hat im Wesentlichen zwei Ursachen. Erstens unterliegen ökonomische Rahmenbedingungen ständigen Änderungen, die wiederum einen wechselnden Einfluss auf den Kurs des Underlying haben. Dessen Volatilitäten sind daher ebenfalls ständigen Schwankungen ausgesetzt. Erwartet beispielsweise ein Analyst für einen zukünftigen Zeitpunkt eine Änderung der ökonomischen Fundamentaldaten, etwa eine Zinsänderung durch einen Bundesbankbeschluss, so wird dies Einfluss auf seine Einschätzung der DAX-Entwicklung haben. Dies führt dazu, dass der Analyst zur Optionspreisbestimmung von Optionen, die vor bzw. nach dem Bundesbankbeschluss auslaufen werden, jeweils unterschiedliche Volatilitäten verwendet. Ein zweiter Grund ist die Mean-Reverting-Eigenschaft der Volatilität. Volatilitäten verharren nicht bei extremen Werten. Vielmehr kehren sie immer wieder zu ihrem langjährigen Durchschnittswert zurück. Grafik 3

3-Entwicklung VDAX

verdeutlicht diese Eigenschaft anhand der Entwicklung des VDAX, einem Index der impliziten Volatilitäten der DAX-Optionen. Der VDAX zeigt die Tendenz, immer wieder zu seinem langjährigen Durchschnitt von 15,44 Prozent zurückzukehren. Sein maximaler Wert betrug 26,56 Prozent, sein minimaler Wert 9,36Prozent.

Berechnung der Forward-Volatilität

Die Zeitstruktur der Volatilität erinnert stark an eine Zinsstrukturkurve. Daher erfolgt die Bestimmung der impliziten Forward-Volatilitäten in Analogie zu einem Forward-Rate-Agreement im Zinsbereich. Die Existenz von Volatilitätssmiles wird zunächst ausgeklammert, das heißt, je Laufzeit existiert nur eine implizite Volatilität.

Grafik 4

4-Forward-Volatilität

zeigt die zu berechnende Forward-Volatilität sowie die dazu zur Verfügung stehenden Größen. Zwischen den einzelnen Größen gilt die folgende Beziehung (stochastische Unabhängigkeit von σ₁ und σ_F unterstellt):

$\left( T_1-T_0 \right) \sigma^2_1 + \left( T_2-T_1 \right) \sigma^2_F = \left( T_2-T_0 \right) \sigma^2_2$

Wird diese Gleichung nach der Forward-Volatilität σ_F aufgelöst, so ergibt sich als Formel für die implizite Forward-Volatilität:

$\sigma_F = \sqrt{\frac{\left( T_2-T_0 \right) \sigma^2_2 - \left( T_1-T_0 \right) \sigma^2_1}{T_2-T_1}}$

Theoretisch ist die so berechnete Forward-Volatilität auch der faire Kurs für einen börsengehandelten Future.

Spezifikationen eines Volatilitätsfutures

Das Underlying

Zunächst ist zu klären, auf welche implizite Volatilität sich der Future bezieht. Je länger die Laufzeit einer Option, desto stärker reagiert ihr Preis auf Volatilitätsänderungen. Unter diesem Aspekt sollte die zugrunde liegende Volatilität sich auf möglichst lang laufende Optionen beziehen. Andererseits sind Optionen mit längerer Restlaufzeit in der Regel weniger liquide als Optionen mit kürzerer Restlaufzeit. Daher sollten als Underlying eher Volatilitäten mit kurzer Restlaufzeit gewählt werden. Einen guten Kompromiss, diesen Gegensatz zu lösen, stellen die impliziten Drei-Monats-Volatilitäten dar.

Aufgrund der Smilestruktur der impliziten Volatilitäten gibt es wie schon in Grafik 1 gezeigt keine einheitliche implizite Drei-Monats-Volatilität. Die am aktivsten gehandelten Optionen sind die Optionen am „at-the-money“-Punkt. Zur Lösung der Smileproblematik ist es daher sinnvoll als Underlying die implizite Volatilität am „at-the-money“-Punkt zu verwenden. Börsengehandelte Optionen sind hinsichtlich der Basispreise standardisiert. Das bedeutet, dass es in der Regel keine Option gibt, deren Basispreis mit dem „at-the-money“-Punkt identisch ist. Die implizite Volatilität am „at-the-money“-Punkt wird daher wie folgt definiert: Sie ist der gewogene Durchschnitt der impliziten Volatilitäten der vier um den „at-the-money“-Punkt liegenden Optionen mit gleicher Restlaufzeit (Grafik 5)

5-Ermittlung at the money Volatilität

. Im Falle des Volax-Futures wurde das Underlying, die Drei-Monats-Volatilität, durch einen Subindex des VDAX berechnet, der zusammen mit dem VDAX und weiteren Subindizes von der Deutschen Börse an Börsentagen alle 15 Sekunden berechnet und veröffentlicht wird.

Laufzeiten des Futures

An der Eurex werden u.a. ständig Optionen auf den DAX mit maximalen Laufzeiten von drei, sechs, neun und zwölf Monaten gehandelt. Aus den impliziten Volatilitäten am „at-the-money“-Punkt dieser Optionen lassen sich mit der im vorherigen Kapitel beschriebenen Formel implizite Drei-Monats-Forward-Volatilitäten mit einem Zeithorizont von drei, sechs und neun Monaten berechnen. Dadurch konnte der Volax-Future auf die implizite Drei-Monats-Volatilität der DAX-Optionen ebenfalls diese drei Laufzeiten aufweisen.

Kontraktwert

Damit der Volatilitätsfuture zur exakten Feinsteuerung des Volatilitätsrisikos eines Optionsportfolios verwendet werden kann, sollte der Kontraktwert nicht zu groß sein. Ein Kontraktwert von 100 DM multipliziert mit dem Kurs des Futures, der mit zwei Nachkommastellen notiert, erfüllte 1998 diese Anforderung. Daraus ergab sich beim Volax-Future eine Tick-Größe von 1 DM.

Verfalltermine

Der Volax-Future verfiel wie die zur Berechnung des Underlying notwendigen Optionen an jedem dritten Freitag der Monate März, Juni, September und Dezember.

Anwendungsbereiche

Hedging

Der Volatilitätsfuture kann zur Absicherung von Optionsportfolios gegen Volatilitätsänderungen verwendet werden. Der Einfluss der Volatilität auf den Optionspreis und damit das Ausmaß des Volatilitätsrisikos wird durch die erste Ableitung der Black/Scholes-Formel nach der Volatilität deutlich:

$\frac{\partial P}{\partial \sigma} = Vega = S \sqrt{t}N'\left(\frac{\ln{\left(\frac{S}{E}\right)} + \left(r + \frac{\sigma^2}{2}\right)t}{\sigma \sqrt{t}}\right)$

Diese Größe wird auch Vega genannt, so dass statt des Begriffes Volatilitätsrisiko auch der Begriff Vegarisiko verwendet wird. Folgendes Zahlenbeispiel verdeutlicht anschaulich die große Bedeutung des Volatilitätsrisikos: Ein Händler möchte vormittags bei einem DAX-Kurs von 3300, einem Zinssatz von 3,4 Prozent und einer Volatilität von 14 Prozent einen DAX-Call mit einem Basispreis von 3300 und einer Laufzeit von 30 Tagen kaufen. Er erhält die Option zu dem rechnerisch fairen Wert von 57,50 DM. Am Nachmittag sind alle Marktparameter unverändert, lediglich die Volatilität ist auf 12 Prozent abgesunken (-14,3Prozent). Der Wert seines Calls sinkt dadurch auf 49,98 DM, immerhin ein Verlust von 13,2 Prozent innerhalb weniger Stunden. Das Volatilitätsrisiko besteht für jedes Optionsportfolio mit Ausnahme von Optionen, die bis zum Verfall gehalten werden. Insbesondere für Market Maker, die verbindliche Kurse stellen und handeln müssen, stellt der Volatilitätsfuture ein sinnvolles Instrument zur Absicherung dar.

Spekulation

Der Volax-Future erlaubte es Tradern erstmalig, auf eine reine Volatilitätsänderung zu spekulieren. Mit den herkömmlichen Optionen ist dies bisher nur in sehr eingeschränkter Weise möglich. Aufgrund des Einflusses einer Vielzahl ökonomischer Kennzahlen auf die impliziten Volatilitäten ergibt sich für Trader ein ganz neues Betätigungsfeld. Auch wurden in den letzten Jahren eine Reihe an vielversprechenden Verfahren zur Volatilitätsprognose entwickelt, die sich in profitable Handelsstrategien einbauen lassen.

Arbitrage

Unter Arbitrage wird die Realisierung risikoloser Gewinne durch das Ausnutzen von Preisunterschieden verstanden. Der Volatilitätsfuture ist auf die folgende Art und Weise arbitragierbar: Ist der Future teurer (preiswerter) als sein rechnerisch fairer Wert, so muss ein Arbitrageur den Future verkaufen (kaufen), die zur Berechnung des fairen Futureskurses notwendige kurzfristige Volatilität mittels eines deltaneutralen Straddles ebenfalls verkaufen (kaufen) und die entsprechende längerfristige Volatilität durch einen deltaneutralen Straddle kaufen (verkaufen). Zur echten Arbitrage müssen die beiden Straddles zusätzlich gegeneinander thetaneutral ausgerichtet werden, damit es im Arbitrageportfolioes nicht zu einem Zeitwertverlust kommt. Zur deltaneutralen Ausbalancierung des Arbitrageportfolios kann auch der DAX-Future verwendet werden. Bei Bewegungen des DAX muss das Arbitrageportfolio dynamisch den sich veränderten Marktbedingungen angepasst werden.

Fazit und Ausblick

Das vorgestellte Konzept Volax-Futures auf die impliziten Drei-Monats-Volatilitäten der DAX-Optionen war 1998 eine echte Finanzinnovation. Erstmals in der Geschichte der Terminbörsen wurde mit diesem Kontrakt der Faktor Volatilität isoliert handelbar. Für Hedger, Spekulanten und Arbitrageure ergaben sich durch den reinen Volatilitätshandel eine Vielzahl neuer Möglichkeiten zur Steuerung ihrer Optionsportfolios. Allgemein wurden und werden Volatilitätsderivaten trotz der Einstellung des Handels Ende 1998 des Volax-Futures mangels Liquidität erhebliche Umsatzpotentiale zugesprochen. Das vorgestellte Konzept des Volax-Futures ist darüber hinaus geeignet, auf die Märkte für Zins-, Währungs- und Commodity-Optionen übertragen zu werden. Dazu muss lediglich das zur Berechnung impliziter Volatilitäten notwendige Optionspreismodell dem jeweiligen Underlying angepasst werden. Zwar hat seit 1998 keine Terminbörse mehr einen neuen Anlauf unternommen, Volatilitätsderivate zu listen, doch haben einige Banken in Deutschland Zertifikate aufgelegt, die nach ganz ähnlichen Prinzipien funktionieren wie der damalige Volax-Future. Hierzu zählen z.B. Zertifikate der Deutschen Bank auf den VDAX oder der UBS auf die implizite Volatilität von DAX-Optionen.

Literatur

• Black, Fischer/Scholes, Myron (1973): The Pricing of Options and Corporate Liabilities, in: Journal of Political Economy, Vol. 81, S. 637-654.
• Brenner, Menachem/Galai, Dan (July-August 1989): New Financial Instruments for Hedging Changes in Volatility, in: Financial Analysts Journal, S. 64.
• Engle, Robert F. (1993): Statistical Models for Financial Volatility, in: Financial Analysts Journal, January-February, S. 72-78. (Eine gute Einführung in die Verfahren zur Volatilitätsprognose)
• Grünbichler, Andreas/Longstaff, Francis A. (1994): Valuing Futures and Options on Volatility, Working Paper, Anderson Graduate School of Management University of California, S. 1ff.
• Manaster, Steven und Koehler, Gary (1982): The Calculation of Implied Variances from the Black-Scholes Model: A Note, in: The Journal of Finance, Vol. 37, S. 227-229.
• Natenberg, Sheldon (1994): Option Volatility and Pricing, New York, S. 72ff.
• Redelberger, Dr. Thomas (1994): Grundlagen und Konstruktion des VDAX-Volatilitätsindex der Deutsche Börse AG. (Achtung, das VDAX-Konzept wurde Ende 1997 grundlegend überarbeitet, der VDAX wird aktuell nach einem anderen Konzept berechnet. Siehe auch [1] für den Indexleitfaden der Deutschen Börse)
• Roth, Randolf (1998): Das theoretische Konzept eines Volatilitätsderivates und seine Anwendung auf die DAX-Optionen, S.1ff.
• Tompkins, Robert (1994): Options Explained2, S.156f. Dort findet sich auch eine Analyse der Smilestrukturen unterschiedlicher Optionsmärkte.
• Werner, Elmar (1997): Future auf implizite Volatilitäten in DAX-Optionen, in: Die Bank, Nr. 6, S.342-345.
• Werner, Elmar/Roth, Randolph (1998): The Volax future, in: Risk - Special Report Equity Derivatives, February, S. S16-S17.
• Whaley, Rober E. (1993): Derivatives on Market Volatility: Hedging Tools Long Overdue, in: The Journal of Derivatives, S. 71ff.