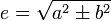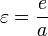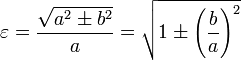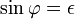Lineare Exzentrizität

Die Exzentrizität ist ein Maß für die Abweichung eines Kegelschnittes von der Kreisform.

• Die lineare Exzentrizität oder Brennweite ist ein Längenmaß.
• Die numerische Exzentrizität ist eine dimensionslose Größe.

Neben allgemeinen Problemen der Geometrie spielen die Werte insbesondere in Optik und Astronomie – hier auch als Exzentrizitätswinkel – eine besondere Rolle

Die lineare Exzentrizität e

Im Zähler der numerischen Exzentrizität steht e, die lineare Exzentrizität. Sie ist ein Maß für die optische Brennweite des Kegelschnitts:

$e = \sqrt{a^2 \pm b^2}$

Im Falle der Parabel ist die Gleichung trivial: e = a und b = 0
Gleichfalls im Falle des Kreises: a = b und e = 0

Die numerische Exzentrizität ε

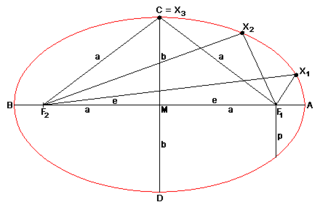Ellipse mit Beschriftung und Brennlinien.
Zu den anderen in der Grafik verwendeten Bezeichnungen siehe Ellipse.

Die numerische Exzentrizität eines Kreises ist 0, die einer Ellipse zwischen 0 und kleiner als 1, die einer Parabel 1 und die einer Hyperbel größer als 1.

Es steht a für die große und b für die kleine Halbachse einer Ellipse bzw. imaginäre Halbachse der Hyperbel.

Die Formel zur Berechnung der numerischen Exzentrizität ist:

$\varepsilon = \frac{e}{a}$

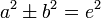Mit $a^2 \pm b^2 = e^2$ (+ für die Hyperbel, − für die Ellipse) ergibt sich:

$\varepsilon = \frac{\sqrt{a^2 \pm b^2}}{a} = \sqrt{1 \pm \left( {b\over a} \right) ^2}$

Die Exzentrizität in der Astronomie

Die numerische Exzentrizität dient in der Himmelsmechanik als Bahnelement der Beschreibung der Form einer Keplerbahn. Sie charakterisiert die verschiedenen Typen der Lösungen des Keplerproblems (Zweikörperproblem).

Zu beachten ist, dass die numerische Exzentrizität ε im astronomischen Gebrauch kurz als „die Exzentrizität“ und mitunter auch mit e bezeichnet wird, da die lineare Exzentrizität (mathematisch e) als absolute Größe nicht verwendet wird, sondern durch die Periapsisdistanz a−e oder den Bahnradius r₀ ersetzt wird.

Für einen Orbit in Form einer Keplerellipse gilt:

1. Die Periapsisdistanz = Große Halbachse − Exzentrizität: r_min = a − e = a(1 − ε)
2. Die Apoapsisdistanz = Große Halbachse + Exzentrizität: r_max = a + e = a(1 + ε)
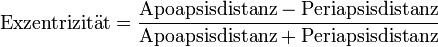3. $\mathrm{Exzentrizit\ddot at} = \frac{\mathrm{Apoapsisdistanz} - \mathrm{Periapsisdistanz}}{\mathrm{Apoapsisdistanz} + \mathrm{Periapsisdistanz}}\;$, d. h.,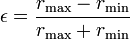 $\quad\epsilon = \frac {r_\mathrm{max} - r_\mathrm{min}} {r_\mathrm{max} + r_\mathrm{min}}$

Für manche Fälle findet auch noch der Exzentrizitätswinkel φ als Bahnelement eine Anwendung:

$\sin \varphi = \epsilon$

Der Exzentrizitätswinkel ist die Abweichung der wahren Anomalie ν des Nebenscheitels S_N vom rechten Winkel.

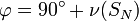$\varphi = {90^\circ + \nu (S_N)}$ oder $\epsilon = \cos \nu (S_N) \,$

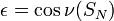
Dieser Zusammenhang eignet sich insbesondere, wenn man direkt mit der Keplergleichung hantiert.

Etymologie: Aus lateinisch ex „außerhalb“ und centrum „Mittelpunkt“ heißt excentricus „außermittig“: Die Bezeichnung geht auf Tycho Brahe zurück: Das sogenannte tychonische Weltsystem ist eine Mischung aus geozentrischem und heliozentrischem Weltbild. Die Erde ist dabei das Zentrum der Welt, um die die Sonne kreist. Die anderen Planeten bewegen sich auf sogenannten „exzentrischen“ Kreisbahnen um der Sonne.

Unter den Planeten unseres Sonnensystems hat die Venus mit 0,0067 die geringste Exzentrizität (also die kreisähnlichste Bahn) und der Merkur mit 0,2056 die größte. Die Werte für die anderen Planeten, unter anderem auch für deren mittlere Entfernung zur Sonne, können in der Tabelle der Planetendaten nachgelesen werden. Die Werte für Aphel- und Periheldistanz können dem Artikel Apsis (Astronomie) entnommen werden.

Siehe auch: Keplersche Gesetze