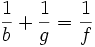Linsenformel

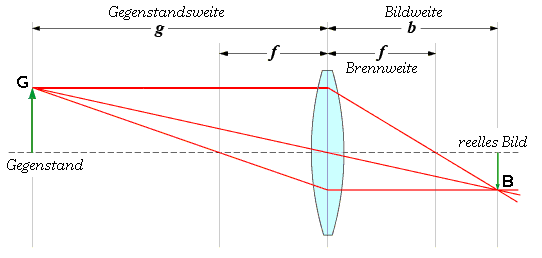
Mit der Linsengleichung, auch Abbildungsgleichung genannt, kann man die optische Abbildung einer idealen Linse berechnen.

Bezeichnungen an der Linse

Wenn man den Strahlensatz der Geometrie zuerst auf den Mittelpunktsstrahl und die sich mit ihm im Mittelpunkt der Linse kreuzende optische Achse anwendet erhält man den Abbildungsmaßstab A (oder β):

$A = \frac{B}{G}= \frac{b}{g}$.

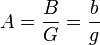Wobei G die Größe des abzubildenden Gegenstandes (Objektes) angibt und B die des Bildes. Die Gegenstandsweite oder Objektweite, also der Abstand zwischen Hauptebene der Linse und Objekt, ist hier mit g bezeichnet, und die Bildweite, also der Abstand zwischen Hauptebene und Bild, mit b.

Wendet man den Strahlensatz der Geometrie nun auf den Brennpunktstrahl und die sich mit ihm im Brennpunkt kreuzende optische Achse an, so erhält man:

$\frac{B}{G} = \frac{b-f}{f}$.

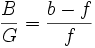f ist in diesem Fall die bildseitige Brennweite der Linse.

Die linken Seiten der 1. und 2. Gleichung sind gleich, also müssen auch die rechten Seiten gleich sein, das ergibt:

$\frac{b}{g}=\frac{b-f}{f}$.

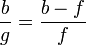Die Division durch b und das Umformen der Gleichung ergibt:

$\frac{1}{b} + \frac{1}{g} = \frac{1}{f}$

Diese Beziehung wird Abbildungsgleichung genannt.

Diese Erklärungen beziehen sich auf eine dünne Linse, bei der die objektseitige und bildseitige Hauptebene zusammenfallen. Die Linsengleichung ist auch für dicke Linsen und Systeme aus mehreren Linsen gültig, deren Hauptebenen im Allgemeinen nicht zusammenfallen. Dann bezeichnet g den Abstand zwischen Objekt und objektseitiger Hauptebene, und b den Abstand zwischen Bild und bildseitiger Hauptebene.

Eine äquivalente Formulierung stellt die Newtonsche Abbildungsgleichung dar. Will man die Brennweite bestimmen, sind das Bessel-Verfahren oder das Abbe-Verfahren vorzuziehen.

Den Zusammenhang zwischen Linsenform und Brennweite hingegen gibt die sogenannte Linsenschleiferformel an..