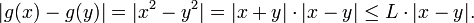- Lipschitz-Bedingung
-
Lipschitz-Stetigkeit (nach Rudolf Lipschitz) ist ein Begriff aus der Analysis.
Inhaltsverzeichnis
Definition
Eine Funktion
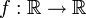 heißt Lipschitz-stetig, wenn eine Konstante L existiert mit
heißt Lipschitz-stetig, wenn eine Konstante L existiert mitDies ist ein Spezialfall der folgenden, allgemeinen Definition.
Seien (X,dX) und (Y,dY) metrische Räume. Eine Funktion
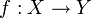 heißt Lipschitz-stetig, falls es eine (nichtnegative) reelle Zahl L gibt, sodass
heißt Lipschitz-stetig, falls es eine (nichtnegative) reelle Zahl L gibt, sodasserfüllt ist. L wird Lipschitz-Konstante genannt. Anschaulich gesprochen, ist die Steigung von f nach oben durch L beschränkt. Ist eine Funktion Lipschitz-stetig, so sagt man auch sie erfülle die Lipschitz-Bedingung.
Eine Abschwächung der Lipschitz-Stetigkeit ist die lokale Lipschitz-Stetigkeit. Eine Funktion
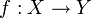 heißt lokal Lipschitz-stetig, wenn es um jeden Punkt in X eine Umgebung gibt, sodass die Einschränkung von f auf diese Umgebung Lipschitz-stetig ist. Eine Funktion die nur auf einer Teilmenge
heißt lokal Lipschitz-stetig, wenn es um jeden Punkt in X eine Umgebung gibt, sodass die Einschränkung von f auf diese Umgebung Lipschitz-stetig ist. Eine Funktion die nur auf einer Teilmenge 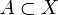 definiert ist, heißt Lipschitz- oder lokal Lipschitz-stetig, wenn sie Lipschitz- oder lokal Lipschitz-stetig bezüglich der metrischen Räume (A,dX | A) und (Y,dY) ist.
definiert ist, heißt Lipschitz- oder lokal Lipschitz-stetig, wenn sie Lipschitz- oder lokal Lipschitz-stetig bezüglich der metrischen Räume (A,dX | A) und (Y,dY) ist.Eigenschaften
Lipschitz-stetige Funktionen sind lokal Lipschitz-stetig. (Wähle ganz X als Umgebung und stets L als Lipschitz-Konstante.) Lokal Lipschitz-stetige Funktionen sind stetig (Wähle
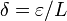 in der
in der  -δ-Definition der gleichmäßigen Stetigkeit.) und entsprechend sind Lipschitz-stetige Funktionen gleichmäßig stetig. Daher ist Lipschitz-Stetigkeit „stärker“ als gleichmäßige Stetigkeit. Die Umkehrung gilt im Allgemeinen nicht, so ist z. B. die Funktion
-δ-Definition der gleichmäßigen Stetigkeit.) und entsprechend sind Lipschitz-stetige Funktionen gleichmäßig stetig. Daher ist Lipschitz-Stetigkeit „stärker“ als gleichmäßige Stetigkeit. Die Umkehrung gilt im Allgemeinen nicht, so ist z. B. die Funktion ![f:[0,1]\rightarrow\R,~x\mapsto\sqrt x](/pictures/dewiki/102/f1e7b068458716f9a259da0fa00d25e0.png) zwar Hölder-stetig mit Exponenten 1 / 2 und daher gleichmäßig stetig, jedoch nicht Lipschitz-stetig (siehe Beispiel).
zwar Hölder-stetig mit Exponenten 1 / 2 und daher gleichmäßig stetig, jedoch nicht Lipschitz-stetig (siehe Beispiel).Nach dem Satz von Rademacher ist eine lipschitzstetige Funktion fast überall differenzierbar. Es gibt jedoch auch Funktionen, die zwar differenzierbar, aber nicht lipschitzstetig sind, z. B.
 . Eine differenzierbare Funktion
. Eine differenzierbare Funktion  mit
mit  ist genau dann lipschitzstetig, wenn ihre erste Ableitung beschränkt ist.
ist genau dann lipschitzstetig, wenn ihre erste Ableitung beschränkt ist.Anwendung
Lipschitz-Stetigkeit ist ein wichtiges Konzept in der Theorie gewöhnlicher Differentialgleichungen, um Existenz und Eindeutigkeit von Lösungen zu beweisen (siehe Satz von Picard-Lindelöf). Abbildungen mit einer Lipschitz-Konstante kleiner als eins nennt man Kontraktion. Diese sind wichtig für den Fixpunktsatz von Banach.
Beispiele
Für eine Lipschitz-stetige Funktion
 ist der Quotient
ist der Quotientmit
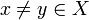 durch jede Lipschitz-Konstante von f nach oben beschränkt. Für lokal Lipschitz-stetige Funktionen ist der Quotient auf hinreichend kleinen Umgebungen beschränkt.
durch jede Lipschitz-Konstante von f nach oben beschränkt. Für lokal Lipschitz-stetige Funktionen ist der Quotient auf hinreichend kleinen Umgebungen beschränkt.Daher ist die Funktion
![f: [0,1]\to\R](/pictures/dewiki/101/e1e8eaf7fd9f12d440ba424134f0b3b8.png) mit
mit 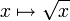 wegen
wegenzwar stetig und sogar gleichmäßig stetig jedoch nicht lokal Lipschitz-stetig und folglich auch nicht Lipschitz-stetig.
Für die Funktion
![g:[a,b]\to\R](/pictures/dewiki/54/6d6d815cc2194078c1799b375d54dc74.png) mit
mit 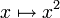 folgt mit
folgt mitdass
Das heißt, L ist eine Lipschitz-Konstante für diese Funktion.
Weil für g der Quotient gleich | x + y | ist, folgt, dass g nur für einen beschränkten Definitionsbereich Lipschitz-stetig ist, für unbeschränkte jedoch nicht.
Wikimedia Foundation.


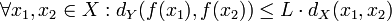
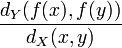
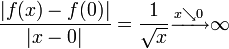
![L:=\max_{x,y \in [a,b]}(|x+y|)=2\max{(|a|,|b|)},](/pictures/dewiki/52/405bc6a6911b5c7ecc19550d0edb5e58.png)