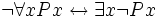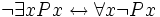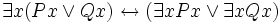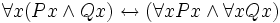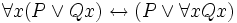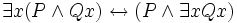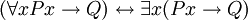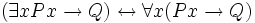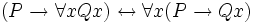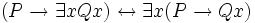Logik erster Ordnung

Die Artikel Prädikatenlogik und Prädikat (Logik) überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Hafenbar 23:36, 2. Mai 2008 (CEST)

Prädikatenlogik oder Quantorenlogik ist eine Familie logischer Systeme, die es erlauben, einen weiten und in der Praxis vieler Wissenschaften und deren Anwendungen wichtigen Bereich von Argumenten zu formalisieren und auf ihre Gültigkeit zu überprüfen. Auf Grund dieser Eigenschaft spielt die Prädikatenlogik eine große Rolle in der formalen und nicht formalen Logik sowie in Mathematik, Informatik, Linguistik und Philosophie.

Prädikatenlogik ist eine Erweiterung der Aussagenlogik. In der Aussagenlogik werden zusammengesetzte Aussagen daraufhin untersucht, aus welchen einfacheren Aussagen sie mit Hilfe von aussageverknüpfenden Bindewörtern – in der Logik: Junktoren – zusammengesetzt sind. Zum Beispiel besteht die Aussage „Es regnet oder die Erde ist eine Scheibe“ aus den beiden Aussagen „Es regnet“ und „Die Erde ist eine Scheibe.“ Diese beiden Aussagen lassen sich ihrerseits nicht in weitere Teilaussagen zerlegen – sie werden deshalb atomar oder elementar genannt. In der Prädikatenlogik werden atomare Aussagen hinsichtlich ihrer inneren Struktur untersucht.

Das zentrale Konzept der Prädikatenlogik ist das Prädikat. Ein Prädikat in diesem prädikatenlogischen Sinn ist eine Folge von Wörtern mit klar definierten Leerstellen (Auslassungen), die zu einer – wahren oder falschen – Aussage wird, wenn in jede Leerstelle ein Eigenname eingesetzt wird. Zum Beispiel ist die deutsche Wortfolge „_ ist ein Mensch“ ein Prädikat, weil durch Einsetzen eines Eigennamens – etwa „Sokrates“ – ein Aussagesatz, zum Beispiel „Sokrates ist ein Mensch“, entsteht. In diesem Sinn lässt sich die elementare Aussage „Die Erde ist eine Scheibe“ prädikatenlogisch in das Prädikat „_ ist eine Scheibe“ und den Eigennamen „die Erde“ zerlegen. Anhand der Definition und der Beispiele wird klar, dass der Begriff „Prädikat“ in der Logik, speziell in der Prädikatenlogik, nicht dieselbe Bedeutung hat wie in der traditionellen Grammatik bzw. Schulgrammatik (auch wenn historisch und philosophisch ein Zusammenhang besteht).

Das charakteristische und wichtigste Sprachmittel der Prädikatenlogik ist der Quantor oder Quantifikator. Quantoren erlauben es, Aussagen darüber zu machen, auf wie viele Individuen ein Prädikat zutrifft. Der Allquantor oder Universalquantifikator sagt aus, dass ein Prädikat auf alle Individuen zutrifft; der Existenzquantor oder Existenzialquantifikator sagt aus, dass ein Prädikat auf mindestens ein Individuum zutrifft. Damit ermöglichen es die Quantoren, Aussagen wie „Alle Menschen sind sterblich“ oder „Es gibt (mindestens) einen rosa Elefanten“ (gleichbedeutend mit: „Es gibt rosa Elefanten“) in ihrer Struktur zu analysieren. Gelegentlich werden zusätzlich numerische Quantoren verwendet, mit denen ausgesagt werden kann, dass ein Prädikat zum Beispiel auf eine genaue Anzahl von Individuen zutrifft; numerische Quantoren lassen sich allerdings auf den All- und den Existenzquantor sowie auf das Identitätsprädikat (meist ausgedrückt durch das Zeichen „=“) zurückführen.

Gottlob Frege und Charles Sanders Peirce^[1] entwickelten unabhängig voneinander die Prädikatenlogik. Frege entwickelt und formalisiert sein System in der 1879 erschienenen Begriffsschrift. Ältere logische Systeme, zum Beispiel die traditionelle Begriffslogik seit ihrer Begründung in der aristotelischen Syllogistik oder auch der modernere Relationenkalkül von Charles Peirce, sind hinsichtlich ihrer Ausdrucksstärke echte Teilmengen der Prädikatenlogik, d. h. sie lassen sich vollständig in dieser ausdrücken bzw. in diese übersetzen.

Prädikate

Die in der Einführung gegebene Definition eines Prädikats als Folge von Wörtern mit klar definierten Leerstellen, die zu einer Aussage wird, wenn in jede Leerstelle ein Eigenname eingesetzt wird, ist eine rein formale, inhaltsfreie Definition. Inhaltlich betrachtet können Prädikate ganz unterschiedliche Gegebenheiten ausdrücken, zum Beispiel Begriffe (z. B. „_ ist ein Mensch“), Eigenschaften (z. B. „_ ist rosa“) oder Relationen, d. h. Beziehungen zwischen Individuen (z. B. „_₁ ist größer als _₂“ oder „_₁ liegt zwischen _₂ und _₃“). Da die genaue Natur und der ontologische Status von Begriffen, Eigenschaften und Relationen umstritten sind bzw. von unterschiedlichen philosophischen Richtungen unterschiedlich betrachtet werden und da auch die genaue Abgrenzung von Begriffen, Eigenschaften und Relationen untereinander unterschiedlich gesehen wird, ist diese formale Definition die anwendungspraktisch günstigste, weil sie es erlaubt, Prädikatenlogik zu verwenden, ohne bestimmte ontologische bzw. metaphysische Voraussetzungen akzeptieren zu müssen.

Die Zahl der unterschiedlichen Leerstellen eines Prädikats wird seine Stelligkeit genannt. So ist ein Prädikat mit einer Leerstelle einstellig, eines mit zwei Leerstellen zweistellig usw. Gelegentlich werden Aussagen als nullstellige Prädikate, d. h. als Prädikate ohne Leerstellen betrachtet. Bei der Zählung der Leerstellen werden nur unterschiedliche Leerstellen berücksichtigt.

In formaler Prädikatenlogik werden Prädikate durch Prädikatbuchstaben ausgedrückt, meist Großbuchstaben vom Anfang des lateinischen Alphabets, zum Beispiel F_₁_₂ für ein zweistelliges Prädikat, G_₁ für ein einstelliges Prädikat oder H_₁_₂_₃ für ein dreistelliges Prädikat. Oft werden die Argumente eines Prädikats in Klammern gesetzt und durch Beistriche getrennt, sodass die genannten Beispiele als F(_₁,_₂) bzw. G(_₁) und H(_₁,_₂,_₃) geschrieben würden.

Eigennamen und Individuenkonstanten

In Sprachphilosophie und Sprachwissenschaft ist das Thema der Eigennamen ein durchaus komplexes. Für die Behandlung im Rahmen einer einleitenden Darstellung der Prädikatenlogik soll es ausreichen, solche Sprachausdrücke als Eigennamen zu bezeichnen, die genau ein Individuum bezeichnen; das Wort „Individuum“ wird hier in einem ganz allgemeinen Sinn verstanden und meint jedes „Ding“ (physikalischer Gegenstand, Zahl, Person,...), das in irgendeiner erdenklichen Weise von anderen Dingen unterschieden werden kann. Eigennamen im genannten Sinn werden meistens eigentliche Eigennamen (z. B. „Gottlob Frege“) oder Kennzeichnungen (z. B. „der gegenwärtige Bundeskanzler von Österreich“) sein.

Das Gegenstück zu den Eigennamen der natürlichen Sprache sind die Individuenkonstanten der Prädikatenlogik; meist wählt man Kleinbuchstaben vom Anfang des lateinischen Alphabets, zum Beispiel a, b, c. Im Gegensatz zu natürlichsprachlichen Eigennamen bezeichnet jede Individuenkonstante tatsächlich genau ein Individuum. Dies bedeutet keine impliziten metaphysischen Voraussetzungen, sondern legt lediglich fest, dass nur solche natürlichsprachlichen Eigennamen mit Individuenkonstanten ausgedrückt werden, die tatsächlich genau ein Individuum benennen.

Mit dem Vokabular von Prädikatbuchstaben und Individuenkonstanten lassen sich aussagenlogisch atomare Sätze wie „Sokrates ist ein Mensch“ oder „Gottlob Frege ist Autor der ‚Begriffsschrift’“ bereits in ihrer inneren Struktur analysieren: Übersetzt man den Eigennamen „Sokrates“ mit der Individuenkonstante a, den Eigennamen „Gottlob Frege“ mit der Individuenkonstante b, den Eigennamen bzw. Buchtitel „Begriffsschrift“ mit der Individuenkonstante c und die Prädikate „_ ist ein Mensch“ und „_₁ ist der Autor von _₂“ mit den Prädikatbuchstaben F_ bzw. G_₁_₂, dann lässt sich „Sokrates ist ein Mensch“ als Fa und „Gottlob Frege ist der Autor der ‚Begriffsschrift’“ mit Gbc ausdrücken.

Quantoren

Hauptartikel: Quantor

Quantoren ermöglichen es, Aussagen darüber zu machen, auf wie viele Individuen ein Prädikat zutrifft. Der Existenzquantor sagt aus, dass ein Prädikat auf mindestens ein Individuum zutrifft, beschreibt also die Existenz mindestens eines unter das Prädikat fallenden Gegenstandes. Der Allquantor sagt aus, dass ein Prädikat auf alle Individuen zutrifft.

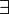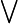Der Existenzquantor wird in halbformaler Sprache als „es gibt mindestens ein Ding, sodass...“ oder „es gibt mindestens ein Ding, für das gilt...“ ausgedrückt. In formaler Sprache werden die Zeichen $\exist$ oder $\bigvee$ verwendet. Der Allquantor wird in halbformaler Sprache als „Für jedes Ding gilt: ...“ ausgedrückt, in formaler Sprache durch eines der Zeichen 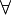$\forall$ oder $\bigwedge$.

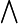Unmittelbar einsichtig ist die Verwendung von Quantoren bei einstelligen Prädikaten, zum Beispiel „_ ist ein Mensch.“ Die existenzquantifizierte Aussage würde lauten „Es gibt mindestens ein Ding, für das gilt: es ist ein Mensch,“ in formaler Sprache: 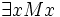$\exists x Mx$. Dabei ist M_ die Übersetzung des einstelligen Prädikats „_ ist ein Mensch“ und ist 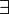$\exists$ der Existenzquantor. Der Buchstabe x ist keine Individuenkonstante, sondern erfüllt dieselbe Funktion, die in der halbformalen Formulierung das Wort „es“ erfüllt: Beide kennzeichnen die Leerstelle, auf die sich der Quantor bezieht. Im gewählten Beispiel erscheint das als redundant, weil es nur einen Quantor und nur eine Leerstelle enthält und daher keine Mehrdeutigkeit möglich ist. Im allgemeinen Fall, in dem ein Prädikat mehr als eine Leerstelle und ein Satz mehr als einen Quantor und mehr als ein Prädikat enthalten kann, wäre ohne die Verwendung geeigneter „Querverweiszeichen“ keine eindeutige Lesart vorgegeben.

Zum Herstellen der Beziehung zwischen einem Quantor und der Leerstelle, auf die er sich bezieht, werden meist Kleinbuchstaben vom Ende des lateinischen Alphabets verwendet, zum Beispiel die Buchstaben x, y und z; sie werden als Individuenvariablen bezeichnet. Die Leerstelle, auf die sich ein Quantor bezieht, bzw. die Variable, die zum Herstellen dieser Verbindung verwendet wird, bezeichnet man als durch den Quantor gebunden.

Bindet man in einem mehrstelligen Prädikat eine Leerstelle durch einen Quantor, dann entsteht ein Prädikat von um eins niedrigerer Stelligkeit. Das zweistellige Prädikat L_₁_₂, „_₁ liebt _₂“, das die Relation des Liebens ausdrückt, wird durch Binden der ersten Leerstelle durch den Allquantor zum einstelligen Prädikat 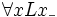$\forall x Lx\_$, sozusagen zur Eigenschaft, von jedem geliebt zu werden (der Allquantor bezieht sich auf die erste Leerstelle, in der das Individuum steht, von dem die Liebe ausgeht). Durch Binden der zweiten Leerstelle wird daraus hingegen das einstellige Prädikat 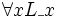$\forall x L\_x$, sozusagen die Eigenschaft, alles und jeden zu lieben (der Allquantor bindet die zweite Leerstelle, also jene, in der das Individuum steht, das die Rolle des oder der Geliebten innehat).

Interessant sind Sätze mit Prädikaten, in denen mehr als eine Leerstelle durch einen Quantor gebunden wird. Die Möglichkeit der Behandlung solcher Sätze macht die große Leistungsfähigkeit der Prädikatenlogik aus, ist aber zugleich der Punkt, an dem das System für den Neueinsteiger etwas kompliziert wird und intensiverer Auseinandersetzung und Übung bedarf. Als kleiner Einblick in die Möglichkeiten der Prädikatenlogik sollen für das einfache zweistellige Prädikat L_₁_₂, das zum Beispiel wie oben gelesen werden kann als „_₁ liebt _₂“, alle Möglichkeiten aufgezählt werden, die Leerstellen durch Quantoren zu binden:

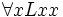1. $\forall x Lxx$: „für jedes Ding gilt: es liebt es (=sich selbst)“: Alles und jeder liebt sich selbst
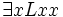2. $\exist x Lxx$: „für mindestens ein Ding gilt: es liebt es (=sich selbst)“: Mindestens einer liebt sich selbst
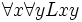3. $\forall x \forall y Lxy$: Jeder liebt jeden
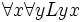4. $\forall x \forall y Lyx$: Jeder wird von jedem geliebt
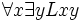5. $\forall x \exist y Lxy$: Jeder liebt mindestens einen
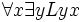6. $\forall x \exist y Lyx$: Jeder wird von mindestens einem geliebt
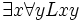7. $\exist x \forall y Lxy$: Es gibt jemanden, der alle liebt
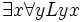8. $\exist x \forall y Lyx$: Es gibt jemanden, der von allen geliebt wird
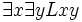9. $\exist x \exist y Lxy$: Mindestens einer liebt mindestens einen
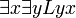10. $\exist x \exist y Lyx$: Mindestens einer wird von mindestens einem geliebt

Wichtig und instruktiv ist es, zwischen den Sätzen 6, 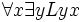$\forall x \exist y Lyx$, und 7, 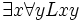$\exist x \forall y Lxy$, zu unterscheiden: In beiden Fällen wird jeder geliebt; im ersten Fall jedoch wird jeder von irgendjemandem geliebt, im zweiten Fall wird jeder von ein und demselben Individuum geliebt.

Zwischen einigen dieser Sätze bestehen Folgerungszusammenhänge, zum Beispiel:

• Aus Satz 3 folgt Satz 4, und aus Satz 4 folgt Satz 3.
• Aus Satz 7 folgt Satz 6 (aber nicht umgekehrt): Wenn es jemanden gibt, der alle liebt, dann wird tatsächlich jeder von mindestens einem geliebt.
• Aus Satz 8 folgt Satz 5 (aber nicht umgekehrt): Wenn es jemanden gibt, der von allen geliebt wird, dann muss tatsächlich jeder mindestens einen lieben.
• Aus Satz 9 folgt Satz 10, und aus Satz 10 folgt Satz 9.

In natürlicher Sprache treten Quantoren in sehr unterschiedlichen Formulierungen auf. Oft werden Wörter wie „alle,“ „keine,“ „einige“ oder „manche“ verwendet, manchmal ist die Quantifizierung nur aus dem Zusammenhang erkennbar – zum Beispiel meint der Satz „Menschen sind sterblich“ in der Regel die Allaussage, dass alle Menschen sterblich sind.

Einige prädikatenlogische Äquivalenzen

Dieses Kapitel stellt exemplarisch einige häufiger gebrauchte prädikatenlogische Äquivalenzen, angezeigt durch den Doppelpfeil, dar.

• $\neg \forall x Px \leftrightarrow \exists x \neg Px$

Sprich: die Verneinung der Aussage „Alle Autos sind grün“ lässt sich wahlweise als „Nicht alle Autos sind grün“ oder als „Es gibt mindestens ein Auto, das nicht grün ist“ formulieren.

• $\neg \exists x Px \leftrightarrow \forall x \neg Px$

Diese Äquivalenz zeigt auf, dass die Verneinung der Aussage „Es gibt mindestens einen Ostfriesen, der die Wahrheit sagt“ wahlweise als „Es ist nicht der Fall, dass es mindestens einen Ostfriesen gibt, der die Wahrheit sagt“ oder als „Alle Ostfriesen sagen nicht die Wahrheit“ ausgedrückt werden kann.

• $\exists x ( Px \vee Qx ) \leftrightarrow (\exists x Px \vee \exists x Qx)$
• $\forall x ( Px \wedge Qx ) \leftrightarrow (\forall x Px \wedge \forall x Qx)$
• $\forall x (P \vee Qx) \leftrightarrow (P \vee \forall x Qx)$
• $\exists x (P \wedge Qx) \leftrightarrow (P \wedge \exists x Qx)$
• $(\forall x Px \rightarrow Q) \leftrightarrow \exists x (Px \rightarrow Q)$
• $(\exists x Px \rightarrow Q) \leftrightarrow \forall x (Px \rightarrow Q)$
• $(P \rightarrow \forall x Qx) \leftrightarrow \forall x (P \rightarrow Qx)$
• $(P \rightarrow \exists x Qx) \leftrightarrow \exists x (P \rightarrow Qx)$

Arten von Prädikatenlogik

Wenn – wie bisher skizziert – Quantoren die Leerstellen von Prädikaten binden, dann spricht man von Prädikatenlogik der ersten Stufe oder Ordnung, englisch: first order logic, abgekürzt FOL; sie ist sozusagen das Standardsystem der Prädikatenlogik.

Eine naheliegende Variation der Prädikatenlogik besteht darin, nicht nur die Leerstellen von Prädikaten zu binden, also nicht nur über Individuen zu quantifizieren, sondern auch Existenz- und Allaussagen über Prädikate zu machen. Auf diese Weise kann man Aussagen wie „Es gibt ein Prädikat, für das gilt: es trifft auf Sokrates zu“ und „Für jedes Prädikat gilt: es trifft auf Sokrates zu, oder es trifft nicht auf Sokrates zu“ formalisieren. Zusätzlich zu den individuellen Leerstellen der Prädikate erster Stufe hätte man auf diese Weise Prädikatsleerstellen eingeführt, die zu Prädikaten zweiter Stufe führen, zum Beispiel eben zu „_ trifft auf Sokrates zu“. Von hier ist es nur ein kleiner Schritt zu Prädikaten dritter Stufe, in deren Leerstellen Prädikate zweiter Stufe eingesetzt werden können, und allgemein zu Prädikaten höherer Stufe. Man spricht in diesem Fall daher von Prädikatenlogik höherer Stufe, englisch higher order logic, abgekürzt HOL.

Die formal einfachste Erweiterung der Prädikatenlogik erster Stufe besteht jedoch in der Ergänzung um Mittel zur Behandlung von Identität. Das entstehende System heißt Prädikatenlogik der ersten Stufe mit Identität. Zwar lässt sich Identität in der Prädikatenlogik höherer Stufe definieren, d. h. ohne Spracherweiterung behandeln, doch ist man bestrebt, möglichst lange und möglichst viel auf der ersten Stufe zu arbeiten, weil es für diese einfachere und vor allem vollständige Kalküle gibt, d. h. Kalküle, in denen alle in diesem System gültigen Formeln und Argumente hergeleitet werden können. Für die Prädikatenlogik höherer Stufe gilt das nicht mehr, d.h. es ist für die höhere Stufe nicht möglich, mit einem einzigen Kalkül alle gültigen Argumente herzuleiten.

Umgekehrt kann man Prädikatenlogik der ersten Stufe einschränken, indem man sich zum Beispiel auf einstellige Prädikate beschränkt. Das aus dieser Einschränkung entstehende logische System, die monadische Prädikatenlogik, hat den Vorteil, entscheidbar zu sein; das bedeutet, dass es mechanische Verfahren (Algorithmen) gibt, die für jede Formel bzw. für jedes Argument der monadischen Prädikatenlogik in endlicher Zeit feststellen können, ob sie bzw. ob es gültig ist oder nicht. Für einige Anwendungszwecke ist monadische Prädikatenlogik ausreichend; zudem lässt sich die gesamte traditionelle Begriffslogik, namentlich die Syllogistik, in monadischer Prädikatenlogik ausdrücken.

Parallel zur bereits thematisierten Unterscheidung prädikatenlogischer Systeme nach ihrer Stufe bzw. Ordnung gibt es klassische und nichtklassische Ausprägungen. Von klassischer Prädikatenlogik bzw. allgemein von klassischer Logik spricht man genau dann, wenn die beiden folgenden Bedingungen erfüllt sind:

• das behandelte System ist zweiwertig, d. h. jede Aussage nimmt genau einen von genau zwei Wahrheitswerten an (Prinzip der Zweiwertigkeit); und
• der Wahrheitswert von Aussagen, die durch aussagenlogische Junktoren zusammengesetzt sind, ist durch die Wahrheitswerte der zusammengesetzten Aussagen eindeutig bestimmt (Extensionalitätsprinzip).

Weicht man von mindestens einem dieser Prinzipien ab, dann entsteht nichtklassische Prädikatenlogik. Selbstverständlich ist es auch innerhalb der nichtklassischen Prädikatenlogik möglich, sich auf einstellige Prädikate zu beschränken (nichtklassische monadische Prädikatenlogik), über Individuen zu quantifizieren (nichtklassische Prädikatenlogik der ersten Stufe), das System um Identität zu erweitern (nichtklassische Prädikatenlogik der ersten Stufe mit Identität) oder die Quantifikation auf Prädikate auszudehnen (nichtklassische Prädikatenlogik höherer Stufe). Ein häufig verwendetes nichtklassisches prädikatenlogisches System ist die modale Prädikatenlogik (siehe Modallogik).

Semantik der Prädikatenlogik

Hauptartikel: Interpretation (Logik)

Wie in formalen Sprachen üblich, wird für die Prädikatenlogik beziehungsweise für jedes prädikatenlogische System eine Interpretation festgelegt, das ist eine Funktion im mathematischen Sinn, die den Zeichen und Ausdrücken der formalen prädikatenlogischen Sprache eine Bedeutung zuordnet. Zunächst wird ein Diskursuniversum festgelegt, das ist die Gesamtheit der unterscheidbaren Gegenstände („Individuen“), auf die sich die zu interpretierenden prädikatenlogischen Aussagen beziehen sollen. Für die klassische Prädikatenlogik werden dann die einzelnen Sprachelemente folgendermaßen interpretiert:

Individuenkonstanten 

Jeder Individuenkonstante wird genau ein Element aus dem Diskursuniversum zugeordnet, das heißt jede Individuenkonstante benennt genau ein Individuum.

Einstellige Prädikate 

Jedem einstelligen Prädikat wird eine Menge von Individuen aus dem Diskursuniversum zugeordnet. Auf diese Weise wird festgelegt, auf welche Individuen das betroffene Prädikat zutrifft. Wird zum Beispiel dem einstelligen Prädikat F die Menge {a,b,c} zugeordnet, dann ist damit festgelegt, dass F auf a, auf b und auf c zutrifft.

Mehrstellige Prädikate 

Jedem n-stelligen Prädikat wird eine Menge von n-Tupeln von Individuen aus dem Diskursuniversum zugeordnet.

Aussagen

Um den Wahrheitswert von Aussagen bestimmen zu können, muss die Bewertungsfunktion die Menge aller wohlgeformten Aussagen in die Menge der Wahrheitswerte abbilden, also für jede Aussage der prädikatenlogischen Sprache festlegen, ob sie wahr oder falsch ist. Dies geschieht in der Regel rekursiv nach folgendem Muster (die Bewertungsfunktion wird hier mit B bezeichnet):

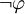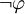• B($\neg\varphi$) = wahr ($\varphi$ ist hier eine prädikatenlogische Aussage), wenn B($\varphi$) = falsch; andernfalls ist B($\neg\varphi$) = falsch. Mit anderen Worten: Die Verneinung einer falschen Aussage ist wahr, die Verneinung einer wahren Aussage ist falsch.
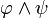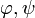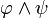• B($\varphi\land\psi$) = wahr ($\varphi, \psi$ sind hier prädikatenlogische Aussagen), wenn B($\varphi$) = B(ψ) = wahr; andernfalls ist B($\varphi\land\psi$) = falsch. Mit anderen Worten: Eine Konjunktion ist genau dann wahr, wenn beide Konjunkte wahr sind; andernfalls ist sie falsch.
• Analoge Definitionen werden für alle anderen Junktoren aufgestellt.
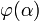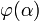• B($\varphi(\alpha)$), wobei $\varphi$ ein einstelliger Prädikatbuchstabe und α eine Individuenkonstante ist, liefert den Wahrheitswert „wahr“, wenn die Interpretation von α ein Element der Interpretation von $\varphi$ ist, mit anderen Worten: wenn das von α benannte Individuum unter das Prädikat $\varphi$ fällt. Andernfalls liefert B($\varphi(\alpha)$) den Wahrheitswert „falsch“.
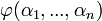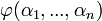• B($\varphi(\alpha_1,...,\alpha_n)$), wobei $\varphi$ ein n-stelliger Prädikatbuchstabe ist und α₁ bis α_n Individuenkonstanten sind, liefert den Wahrheitswert „wahr“, wenn das n-Tupel < α₁,...,α_n > Element der Interpretation des Prädikatbuchstaben $\varphi$ ist. Andernfalls liefert B($\varphi(\alpha_1,...,\alpha_n)$) den Wahrheitswert „falsch“.
• B(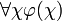$\forall \chi \varphi(\chi)$), wobei χ eine Individuenvariable ist und wobei 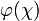$\varphi(\chi)$ ein einstelliges Prädikat ist, in dessen (ein- oder mehrfach vorkommender) Leerstelle χ eingetragen ist, liefert den Wahrheitswert „wahr“, wenn B(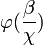$\varphi({\beta\over\chi})$) – dabei ist β – eine Individuenkonstante, die nicht in 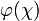$\varphi(\chi)$ vorkommt und ist 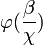$\varphi({\beta\over\chi})$ der Ausdruck, der entsteht, wenn man in 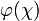$\varphi(\chi)$ jedes Vorkommnis der Individuenvariable χ durch die Individuenkonstante β ersetzt – unabhängig davon, für welches Individuum β steht, den Wahrheitswert „wahr“ liefert; andernfalls ist B(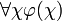$\forall \chi \varphi(\chi)$) = falsch. Mit anderen Worten: B(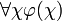$\forall\chi\varphi(\chi)$) ist genau dann wahr, wenn $\varphi$ tatsächlich auf alle Individuen des Diskursuniversums zutrifft.
• B(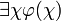$\exists \chi \varphi(\chi)$), wobei χ eine Individuenvariable ist und wobei 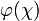$\varphi(\chi)$ ein einstelliges Prädikat ist, in dessen (ein- oder mehrfach vorkommender) Leerstelle χ eingetragen ist, liefert den Wahrheitswert „wahr“, wenn, wenn $\varphi$ auf mindestens ein Individuum aus dem Diskursuniversum zutrifft, das heißt wenn es möglich ist, einer in $\varphi$ nicht vorkommenden Individuenkonstante β ein Individuum aus dem Diskursuniversum derart zuzuordnen, dass B($\varphi({\beta\over\chi})$) 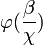den Wahrheitswert „wahr“ liefert.

Alternativen

Vor dem Aufblühen von Aussagenlogik und Prädikatenlogik dominierte die Begriffslogik in Gestalt der von Aristoteles entwickelten Syllogistik und darauf aufbauender relativ moderater Erweiterungen. Zwei in den 1960-er-Jahren in der Tradition der Begriffslogik entwickelte Systeme werden von ihren Vertretern als der Prädikatenlogik gleichmächtig (Freytag) bzw. sogar überlegen (Sommers) bezeichnet, haben aber in der Fachwelt wenig Resonanz gefunden (siehe Artikel Begriffslogik).

Die Gesetze der Prädikatenlogik gelten nur dann, wenn der Bereich der untersuchten Individuen nicht leer ist, d. h. wenn es überhaupt mindestens ein Individuum (welcher Art auch immer) gibt. Eine Modifikation der Prädikatenlogik, die dieser Existenzvoraussetzung nicht unterliegt, ist die Freie Logik (engl. free logic).

Anwendung

Neben der Anwendung als Hilfsmittel vor allem für Informatik, Mathematik und Linguistik spielt die Prädikatenlogik insbesondere in der Konzeption und Programmierung von Expertensystemen und in der künstlichen Intelligenz eine Rolle. In den beiden letztgenannten Gebieten wird oft sogar eine Form angewandter Prädikatenlogik, Prolog („programming in logic“), als Programmiersprache verwendet.

Eine Form der Wissensrepräsentation kann mit einer Sammlung von Ausdrücken in Prädikatenlogik erfolgen.

Der Relationenkalkül, eine der theoretischen Grundlagen von Datenbankabfragesprachen wie etwa SQL, bedient sich ebenfalls der Prädikatenlogik als Ausdrucksmittel.

Siehe auch

Arten und Erweiterungen

Die einzelnen Arten und Erweiterungen der Prädikatenlogik sind in folgenden vertiefenden Einzelartikeln beschrieben:

• Klassische Prädikatenlogik und ihre Erweiterungen
  • Prädikatenlogik der ersten Stufe
  • Prädikatenlogik der ersten Stufe mit Identität
  • Prädikatenlogik höherer Stufe

• Nichtklassische Erweiterungen der Prädikatenlogik
  • Modallogik (modale Prädikatenlogik)
  • Temporale Logik
  • Aktionslogik
  • Fixpunktlogik

Kalküle für prädikatenlogische Systeme

Konkrete Kalküle für prädikatenlogische Systeme werden in folgenden weiterführenden Einzelartikeln angegeben:

• Hilbertkalküle (axiomatischer Kalkül)
• Systeme natürlichen Schließens, zum Beispiel der Fitchkalkül
• Baumkalküle
• Resolution (Logik)
• Existential Graphs
• Dialogische Logik

Quellen

1. ↑ Eric M. Hammer: Semantics for Existential Graphs, Journal of Philosophical Logic, Volume 27, Issue 5 (Oktober 1998), Seite 489: „Development of first-order logic independently of Frege, anticipating prenex and Skolem normal forms“

Literatur

Einführungen

• Jon Barwise, John Etchemendy: Band 1: Aussagen- und Prädikatenlogik. Mentis 2005, ISBN 3-89785-440-6; Band 2: Anwendungen und Metatheorie. Mentis 2006, ISBN 3-89785-441-4
• Benson Mates: Elementare Logik - Prädikatenlogik der ersten Stufe. Vandenhoeck & Ruprecht Göttingen 1997, ISBN 3-525-40541-3
• Wesley C. Salmon: Logik. Stuttgart: Reclam 1983 (=Universal-Bibliothek), ISBN 3-15-007996-9

Zur Geschichte

• Karel Berka, Lothar Kreiser: Logik-Texte. Kommentierte Auswahl zur Geschichte der modernen Logik. Akademie-Verlag Berlin, 4. Auflage 1986
• William Kneale, Martha Kneale: The Development of Logic. Clarendon Press, 1962, ISBN 0-19-824773-7 – Standardwerk zur Geschichte der Logik, in englischer Sprache

Weblinks

• Formale Darstellung der Prädikatenlogik (Technische Universität Dortmund)
• Einführung in die Prädikatenlogik (Universität Wien)
• Einführungsskriptum (PDF-Datei, ETH Zürich)