- Lot (Mathematik)
-
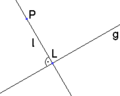
In der Geometrie ist ein Lot von einem Punkt P auf eine Gerade g diejenige Gerade l, die durch den Punkt P geht und die Gerade g senkrecht (in einem 90°-Winkel) schneidet. Der Lotfußpunkt L ist der Schnittpunkt der Geraden g mit dem Lot l, also derjenige Punkt auf g, dessen Abstand zu P minimal ist. Man definiert den Abstand von P zu g als den Abstand von P zu L.
Abweichend von dieser Definition verstehen manche Autoren unter dem Lot von P auf g nicht die Gerade l (siehe oben), sondern die Verbindungsstrecke zwischen P und dem Fußpunkt L. Eindeutig in dieser Hinsicht sind die ebenfalls üblichen Begriffe Lotgerade und Lotstrecke.
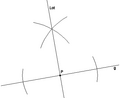
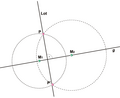
Je nachdem, ob der gegebene Punkt P auf der Geraden g oder außerhalb liegt, spricht man vom Errichten oder vom Fällen des Lotes. In beiden Fällen lässt sich das Lot auf einfache Weise mit Zirkel und Lineal konstruieren.
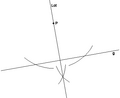
Es gibt eine noch einfachere Methode, um von einem gegebenen Punkt ein Lot auf die Gerade zu fällen. Diese Konstruktion kommt mit nur zwei (beliebigen) Zirkeleinstichen auf der Geraden g aus und kann auch für Spiegelungen benutzt werden (siehe Bild).
In der analytischen Geometrie lässt sich der Fußpunkt L des Lotes von einem Punkt P auf eine Gerade g rechnerisch durch eine Hilfsebene ermitteln, die orthogonal zu der Geraden g ist und den Punkt P enthält. Der Lotfußpunkt ist der Schnittpunkt dieser Hilfsebene mit der Geraden g.
Verallgemeinerung
In der räumlichen Geometrie wird der Begriff Lot auch für Geraden verwendet, die zu einer gegebenen Ebene im Raum senkrecht verlaufen. In ähnlicher Weise spricht man von den Lotebenen einer gegebenen Ebene oder einer Geraden. In der linearen Algebra verallgemeinert man diesen Begriff für beliebige euklidische Räume.
Wikimedia Foundation.