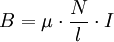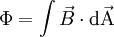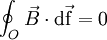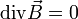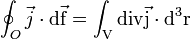- Magnetische Flußdichte
-
Physikalische Größe Name Magnetische Flussdichte Formelzeichen der Größe B Größen- und
Einheiten-
systemEinheit Dimension SI Tesla (T) M/(I·T2) Die magnetische Flussdichte, auch als magnetische Induktion bezeichnet, umgangssprachlich und unpräzise manchmal auch Magnetfeld genannt, ist eine physikalische Größe. Sie hat das Formelzeichen B und steht für die Flächendichte des magnetischen Flusses welcher durch ein bestimmtes Flächenelement hindurch tritt. Das Formelzeichen geht zurück auf den schottischen Physiker James Clerk Maxwell, der in seinen Aufzeichnungen die Buchstaben B, C und D für das magnetische und E, F und G für das elektrische Feld verwendete.
Die Flussdichte
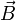 ist eine gerichtete Größe, also ein Vektor und wird aus dem Vektorpotential
ist eine gerichtete Größe, also ein Vektor und wird aus dem Vektorpotential 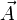 hergeleitet.
hergeleitet.Definition
Die magnetische Flussdichte ist eine Größe der Elektrodynamik. Sie ist der Quotient aus der Lorentzkraft F, die ein vom Strom I durchflossener Leiter der Länge l in einem Magnetfeld erfährt, und dem Produkt dieser Stromstärke I und Leiterlänge l. Dabei orientieren sich die Feldlinien senkrecht zum Strom:
wobei
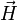 die magnetische Feldstärke,
die magnetische Feldstärke,- μ die Permeabilität ist.
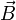 ist ein Vektor, der die Richtung der magnetischen Feldlinien eines Magnetfelds hat.
ist ein Vektor, der die Richtung der magnetischen Feldlinien eines Magnetfelds hat.Die Einheit der magnetischen Flussdichte ist im SI das Tesla mit dem Einheitenzeichen T:
Eine der veralteten Einheiten für die magnetische Flussdichte ist Gauß mit dem Einheitenzeichen G. Gauß wird in der Technik noch immer häufig verwendet. Es gilt 1 T = 10000 G.
Im Zentrum von Spulen, die von Strom mit der Stromstärke I durchflossen werden, die Windungszahl N, die Länge l und die Permeabilität μ haben, herrscht folgende magnetische Flussdichte:
Die Flussdichte ist über folgende Beziehung mit dem magnetischen Fluss verknüpft:
Dass die Flusslinien des magnetischen Flusses in sich geschlossen sind, lässt sich mathematisch dadurch zum Ausdruck bringen, dass jedes Integral von
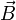 über eine beliebige geschlossene Oberfläche O verschwindet:
über eine beliebige geschlossene Oberfläche O verschwindet:Der nach außen gerichtete Normalenvektor
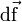 beschreibt an jeder Stelle auf O das orientierte und hinreichend kleine Flächenelement, sein Betrag entspricht jeweils dessen (infinitesimalen bzw. hinreichend kleinen) Flächeninhalt. Die Gleichung folgt aus der Quellenfreiheit des magnetischen Feldes, mathematisch aus der homogenen Maxwellschen Gleichung
beschreibt an jeder Stelle auf O das orientierte und hinreichend kleine Flächenelement, sein Betrag entspricht jeweils dessen (infinitesimalen bzw. hinreichend kleinen) Flächeninhalt. Die Gleichung folgt aus der Quellenfreiheit des magnetischen Feldes, mathematisch aus der homogenen Maxwellschen Gleichungund dem Gaußschen Satz
für ein beliebiges Vektorfeld
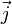 und das in O eingeschlossene Volumen V .
und das in O eingeschlossene Volumen V .Anschaulich: Was (netto) „in V entspringt“, fließt durch O nach außen, was netto „in V versickert“, fließt durch O nach innen.
Die magnetische Flussdichte kann mit Hilfe von Hallsensoren oder Messspulen ermittelt werden.
Literatur
- Küpfmüller, K., Kohn, G., Theoretische Elektrotechnik und Elektronik, Eine Einführung, Springer, 16., vollst. neu bearb. u. aktualisierte Aufl., 2005, ISBN 3-540-20792-9
Wikimedia Foundation.


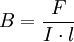
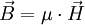
![\left[ B \right] = 1\,{\mathrm{kg} \over \mathrm{As^2}} = 1\,{\mathrm{N} \over \mathrm{Am}} = 1\,{\mathrm{Nm} \over \mathrm{Am^2}} = 1\,{\mathrm{J} \over \mathrm{Am^2}} = 1\,{\mathrm{Ws} \over \mathrm{Am^2}} = 1\,{\mathrm{Vs} \over \mathrm{m^2}} = 1\,\mathrm{T}](/pictures/dewiki/54/6d77349ff5f8caf12bdaacbc005f972c.png)