Martingal

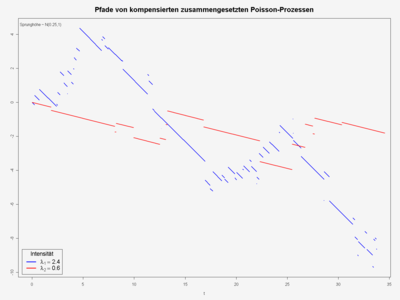Pfade von zwei kompensierten zusammengesetzten Poisson-Prozessen. Die Intensität (Sprunghäufigkeit) des blauen Prozesses ist mit 2.4 genau vier mal so hoch wie die des roten Prozesses. Im gezeichneten Intervall [0,35] springt der blaue Prozess 66 mal, der rote 16 mal, also circa viermal so oft. Bei beiden Prozessen sind die Sprünge normalverteilt mit Mittel 0.25. Diese Sprünge nach oben werden durch die negative Drift genau so ausgeglichen (kompensiert), dass beide Prozesse Martingale sind. Da der blaue Prozess öfter nach oben springt, ist seine negative Drift stärker.

In der Wahrscheinlichkeitstheorie ist ein Martingal ein stochastischer Prozess, bei dem der bedingte Erwartungswert einer Beobachtung gleich dem Wert der vorigen Beobachtung ist.

In die Mathematik wurden Martingale von Paul Pierre Lévy eingeführt.

Definition

Zeitdiskreter Fall

Auf einem Wahrscheinlichkeitsraum $(\Omega, \mathcal{A}, P)$ sei eine Folge $(M_0, M_1, \ldots)$ integrierbarer Zufallsvariablen gegeben, d. h., für alle $n \in \N_0$ gelte $E(|M_n|) < \infty$. Diese Folge heißt ein Martingal, wenn für alle $n \in \N_0$ der bedingte Erwartungswert einer zukünftigen Beobachtung M_{n + 1} gleich dem zuletzt beobachteten Wert ist, also

$E(M_{n+1} \mid M_0, M_1, \dots, M_n) = M_n.$

Diese Bedingung kann so interpretiert werden, dass ein Martingal ein faires Spiel ist, da der Erwartungswert einer zukünftigen Beobachtung gleich der letzten getätigten Beobachtung ist. Wenn der Wert eines Martingals zum Zeitpunkt n bekannt ist, dann ist der Erwartungswert zukünftiger Beobachtungen nicht von Werten abhängig, die vor n beobachtet wurden. Damit gilt noch nicht zwingend die Markow-Eigenschaft, dass die Verteilung von M_{n + 1} lediglich von M_n abhängt. Zum Beispiel kann die Streuung des Martingals auch von Beobachtungen vor n abhängen.

Die Information, die zum Zeitpunkt n über den stochastischen Prozess $(M_n)_{n\in\N_0}$ bekannt ist, kann allgemeiner durch eine Filtrierung gegeben sein. Eine Filtrierung ist eine Folge $(\mathcal F_n)_{n\in\N_0}$ von σ-Algebren, die aufsteigend geordnet ist, d. h. für alle $n \in \N_0$ gilt $\mathcal F_n \subseteq \mathcal F_{n+1}$. Der integrierbare Prozess $(M_n)_{n\in\N_0}$ heißt Martingal bezüglich der Filtrierung $(\mathcal F_n)_{n\in\N_0}$, wenn gilt:

• Für alle $n \in \N_0$ ist M_n messbar bezüglich $\mathcal F_n$ (man sagt dazu „der Prozess ist an die Filtrierung adaptiert“) und
• für alle $n \in \N_0$ gilt die Martingalgleichung $E(M_{n+1} \mid \mathcal F_n) = M_n$.

Der oben betrachtete Fall eines Martingals „schlechthin“ ist in dieser Definition enthalten. Man wähle dazu für $\mathcal F_n$ die von $M_0, \dots, M_n$ erzeugte σ-Algebra $\sigma(M_0, \dots, M_n)$.

Verallgemeinerung auf allgemeine Indexmengen

Sei $(M_t)_{t \in T}$ ein stochastischer Prozess auf einem Wahrscheinlichkeitsraum $(\Omega, \mathcal{A}, P)$ mit einer beliebigen, geordneten Indexmenge T.

$(M_t)_{t \in T}$ heißt ein Martingal bezüglich einer Filtrierung $(\mathcal{F}_t)_{t \in T}$, wenn gilt:

• Für alle $t \in T$ ist M_t messbar bezüglich $\mathcal{F}_t$,
• für jedes $t \in T$ gilt $E(|M_t|) < \infty$, und
• für alle $s, t \in T$ mit $s \le t$ gilt $E(M_t \mid \mathcal{F}_s) = M_s$ (P-fast sicher).

Der zeitdiskrete Fall ist in dieser allgemeinen Definition für $T = \N_0$ enthalten, denn aus $E(M_{n+1} \mid \mathcal F_n) = M_n$ für alle $n \in \N_0$ folgt induktiv $E(M_{m} \mid \mathcal F_n) = M_n$ für alle $m,n \in \N_0$ mit $n \leq m$. Besonders wichtig ist weiterhin der Fall $T = [0,\infty)$ beliebiger nichtnegativer Zeitpunkte als Indexmenge.

Sub- und Supermartingal

Als Submartingal bezeichnet man einen adaptierten und integrierbaren stochastischen Prozess X_t, der im Gegensatz zum Martingal tendenziell steigt:

$E(X_t \mid \mathcal{F}_s) \geq X_s \;\; \mbox{für alle} \; s<t$

Dementsprechend ist ein Supermartingal ein adaptierter und integrierbarer stochastischer Prozess X_t, der tendenziell fällt:

$E(X_t \mid \mathcal{F}_s)\leq X_s\;\; \mbox{für alle} \; s<t$

Motivierendes Beispiel

Der Begriff des Martingals lässt sich als Formalisierung und Verallgemeinerung eines fairen Glücksspiels auffassen. Sei dazu M₀ das Startkapital des Spielers. Dieses wird in vielen Fällen eine Konstante sein, aber auch ein zufälliges Startkapital ist denkbar. Der zufällige Gewinn im ersten Spiel werde mit X₁ bezeichnet. Er kann positiv, null oder negativ (also ein Verlust) sein. Das Kapital des Spielers nach dem ersten Spiel beträgt M₁ = M₀ + X₁ und allgemein nach dem n-ten Spiel

$M_n = M_0 + \sum_{k=1}^n X_k,$

wenn X_k den Gewinn im k-ten Spiel bezeichnet. Bei einem fairen Glücksspiel ist der Erwartungswert jedes Gewinns gleich null, d. h., es gilt E(X_k) = 0 für alle $k\in\N$.

Der Spielverlauf werde nun bis zum Zeitpunkt n einschließlich beobachtet, d. h. die Kapitalstände $M_0, M_1, \dots, M_n$ seien bekannt. Falls nun der Gewinn im nächsten, also im n + 1-ten, Spiel unabhängig vom bisherigen Spielverlauf ist, dann berechnet sich das erwartete Gesamtkapital M_{n + 1} = M_n + X_{n + 1} nach dem nächsten Spiel unter Berücksichtigung aller zur Verfügung stehenden Informationen mit Hilfe der Rechenregeln für bedingte Erwartungswerte zu

$E(M_{n+1} \mid M_0,\dots,M_n) = E(M_n \mid M_0, \dots M_n) + E(X_{n+1} \mid M_0,\ldots,M_n) = M_n + E(X_{n+1}) = M_n.$

Damit ist gezeigt, dass sich das Kapital eines Spielers, der an einem fairen Glücksspiel teilnimmt, als Martingal modellieren lässt.

Bei realen Gücksspielen, wie beispielsweise beim Roulette, ist jedoch wegen des Bankvorteils der erwartete Gewinn bei jedem Spiel im Allgemeinen negativ, also E(X_k) < 0. Dann ergibt sich analog zur obigen Rechnung

$E(M_{n+1} \mid M_0,\dots,M_n) \leq M_n.$

Aus Sicht des Spielers handelt es sich in diesem Fall um ein Supermartingal (Merkspruch: „Supermartingale sind super für die Spielbank“).

Beispiele für zeitstetige Martingale

Wiener-Prozess als Beispiel für ein Martingal

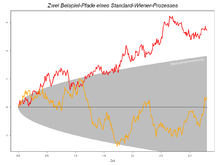
• Ein Wiener-Prozess W_t ist ein Martingal, ebenso sind für einen Wiener-Prozess W_t die Prozesse $W_t^2 - t$ und die geometrische brownsche Bewegung ohne Drift $a \exp\left(\sigma W_t - \frac{\sigma^2}{2}t\right)$ Martingale.
• Ein Poisson-Prozess mit Rate λ, der um seine Drift bereinigt wird, also $\hat P_{\lambda,t}=P_{\lambda,t}-\lambda t$, ist ein Martingal.
• Nach dem Lemma von Itō gilt: Jedes Itō-Integral (mit beschränktem Integranden) ist ein Martingal. Nach dem Itoschen Martingaldarstellungssatz lässt sich umgekehrt jedes Martingal (sogar jedes lokale Martingal) bezüglich einer von einer Brownschen Bewegung erzeugten Filtration als Ito-Integral bezüglich ebendieser Brown'schen Bewegung darstellen.
• Jedes stetige Martingal ist entweder von unendlicher Variation oder konstant.
• Jedes gestoppte Martingal ist wieder ein Martingal.

Gestoppte Brownsche Bewegung als Beispiel für ein Martingal

Quadratische Variation und Exponentialmartingal

Ist die quadratische Variation $\langle M\rangle$ eines stetigen beschränkten Martingals M_t (oder eines mit endlichen exponentiellen Momenten) endlich, so ist der stochastische Prozess

$X_t = M_t^2 - \langle M \rangle_t$

ebenfalls ein Martingal.

Ebenso ist das sog. Exponentialmartingal von M_t, gegeben durch

$X_t=e^{\left(M_t-\frac{1}{2}\langle M\rangle_t\right)},$

ein Martingal.

Herkunft des Wortes

Die Martingale ist eine seit dem 18. Jahrhundert bekannte Strategie im Glücksspiel, bei der nach einem verlorenen Spiel der Einsatz erhöht, im einfachsten Fall verdoppelt wird, so dass im hypothetischen Falle unerschöpflichen Vermögens, unerschöpflicher Zeit, und der Nichtexistenz eines Höchsteinsatzes sicherer Gewinn einträte.^[1]

Da die Martingale das bekannteste Spielsystem war und ist, wurde der Begriff auch als Synonym für „Spielsystem“ gebraucht und fand so Eingang in die mathematische Literatur ^[2].

Das Wort „Martingale“ selbst stammt aus dem Provenzalischen und leitet sich von der französischen Stadt Martigues im Departement Bouches du Rhone am Rande der Camargue ab, deren Einwohner früher als etwas naiv galten. Der provenzalische Ausdruck jouga a la martegalo bedeutet so viel wie sehr waghalsig zu spielen.

Der „Martingal“ genannte Hilfszügel soll ebenfalls nach der Stadt Martigues benannt sein, hiebei handelt es sich um einen optionalen Teil der Pferdeausrüstung, der das Pferd daran hindern soll, den Kopf nach oben zu reißen und zu steigen. Dass dieser Hilfszügel ebenfalls Martingal genannt wird, war den Pionieren der Martingaltheorie nicht bekannt ^[3] – und hat mit der mathematischen Begriffsbildung nichts zu tun.

Siehe auch

• Doob-Zerlegung
• Lokales Martingal
• Semimartingal

Literatur

Historische Literatur

• P. Lévy: Calcul de probabilités. Gauthier-Villars, Paris 1925.
• J. L. Doob: Stochastic Processes. Wiley, New York 1953.

Einführungen

• D. Williams: Probability with Martingales. Cambridge University Press, Cambridge 1991.
• H. Bauer: Wahrscheinlichkeitstheorie. deGruyter, 1991.

Diskrete Martingale

• J. Neveu: Discrete-Parameter Martingales. North-Holland, Amsterdam 1975.
• Y. S. Chow und H. Teicher: Probability Theory: Independence, Interchangeability, Martingales. Springer, New York 1997.

Stetige Martingale

• C. Dellacherie, P.-A. Meyer: Probabilités et potentiel I-IV, Hermann Paris, 1975-1987. (Englische Übersetzung bei North Holland.)

Anwendungen

• R. Bouss: Optimierung des Kreditgeschäftes mit Martingalen. Haupt, Bern 2003.

Einzelnachweise

1. ↑ H. Bauer: Wahrscheinlichkeitstheorie. de Gruyter, Berlin 1991, S. 144.
2. ↑ http://www.jehps.net/juin2009/Mansuy.pdf The Origins of the Word "Martingale"
3. ↑ http://www.jehps.net/juin2009/Mansuy.pdf a.a.O. p.2