Mathematischer Koprozessor

80287, FPU einer 80286 CPU mit 6 MHz.

Gleitkommaeinheit ist ein Begriff aus der Computertechnik und bezeichnet einen speziellen Prozessor, der mathematische Funktionen oder Gleitkommazahlen verarbeitet. Bei vielen modernen CPUs ist die FPU als Koprozessor realisiert. FPU oder NPU sind Abkürzungen für Floating Point Unit beziehungsweise Numeric Processing Unit, oft auch als mathematischer (Ko-)Prozessor oder auch Floating Point Processing Unit (Gleitkommaeinheit) bezeichnet.

Die FPU kann als externer Chip in einem eigenen Gehäuse sitzen (z. B. Intel 80287), oder in einen bestimmten Bereich innerhalb der CPU integriert sein (z. B. Intel Pentium).

Frühe CISC-Prozessoren verfügten oft nicht über eingebaute Mechanismen zur Behandlung von Gleitkommazahlen. Gleitkommaberechnungen und mathematischen Funktionen wurden per Software durch den Hauptprozessor erledigt, was einerseits den Hauptprozessor beanspruchte und andererseits erheblich langsamer als eine spezialisierte Hardwarelösung war. Daher gab es bei CISC-CPUs wie den Intel x86-Prozessoren (bis zum 486er) oder den Motorola 68k-CPUs die Möglichkeit, einen zusätzlichen Koprozessor auf dem Motherboard nachzurüsten. Mit den sinkenden Kosten in der Produktion von Prozessoren sowie durch neuere CPU-Designs (z. B. RISC) sind heute FPUs fest in den CPUs integriert.

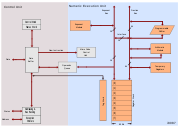
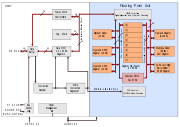
Funktionsweise und Aufbau

Architektur der FPU i8087 beziehungsweise i80287.

Architektur der FPU i80387 mit 16-Bit-Barrel-Shifter und CORDIC-Einheit

Die Anwesenheit einer FPU ermöglicht einen erheblichen Leistungssprung für gleitkommaintensive Berechnungen. So bietet der Koprozessor breitere Register; schon bei 16- und 32-Bit-CPUs hatte die FPU oft bereits 64-Bit, 80-Bit oder auch 128-Bit, so dass einfache Berechnungen mit höherer Genauigkeit durchgeführt werden können und ein größerer Wertebereich abgedeckt wird. Da auch die FPU im Inneren letztendlich eine digitale Recheneinheit darstellt, bedarf es weiterer, trickreicher Methoden, um eine echte Beschleunigung zu erhalten. Viele Modelle (z. B. der 80x87) verfügen über hardwareseitig optimierte Rechenmethoden, wie z. B. den CORDIC-Algorithmus für trigonometrische Funktionen, welcher nur durch Addition und Registerverschiebung, aber ohne langwierige Multiplikation auskommt. Oft wird eine große Beschleunigung auch über fest implementierte Lookup-Tabellen erreicht. Das heißt, die Werte werden nicht über langwierige Iterationen ermittelt, sondern zuerst mit Hilfe von Tabellen näherungsweise und dann durch Interpolationsverfahren bis zu hinreichender Genauigkeit ermittelt. (Eine fehlerhafte Tabelle war übrigens Ursache bei dem berühmten Pentium-Bug.) Weiterhin kann eine FPU ihre Register oftmals als Matrizen organisieren und so Vektorrechnungen beschleunigen.

Die meisten FPUs stellen Operationen für die Grundrechenarten (mit höherer Genauigkeit als die CPU), Logarithmus-, Wurzel- und Potenzrechnung und trigonometrische Funktionen, sowie Funktionen für das Rechnen mit Matrizen zur Verfügung.

Die Rechnenleistung einer FPU wird meistens in FSPEC gemessen, im Gegensatz zu den SPEC einer CPU.

Siehe auch

• Liste x86er-Koprozessoren

Weblinks

• Assembler X86 Befehlslisten/OpCode und Beschreibungen