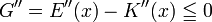Mengenanpassung

In der Theorie der Volkswirtschaftslehre (Mikroökonomie) wird ein Anbieter als Mengenanpasser bezeichnet, wenn er den herrschenden Marktpreis als gegeben akzeptiert und seine Absatzmenge diesem Preis anpasst. Unter der Voraussetzung, dass dieser Anbieter Gewinnmaximierung anstrebt, soll die Differenz aus Erlös und variablen Stückkosten maximiert werden. Angeboten wird nur dann, wenn diese Differenz über den Fixkosten liegt. Im vollkommenen Wettbewerb agieren alle Anbieter als Mengenanpasser, da keiner über hinreichende Marktmacht zur Beeinflussung des Preises verfügt.

Formale Darstellung

Das Problem der Gewinnmaximierung lässt sich bei der Mengenanpassung so formulieren:

Bestimme die optimale Absatzmenge x, so dass der Gewinn G(x) = E(x) - K(x) maximal ist. Dabei bezeichnet E(x)=px die Erlösfunktion für den gegebenen Marktpreis p und K(x) die Kostenfunktion in Abhängigkeit von der produzierten Menge.

Ein Maximum liegt genau dann vor, wenn

1. die erste Ableitung der Gewinnfunktion gleich Null ist:

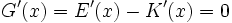$G^\prime(x) = E^\prime(x) - K^\prime(x) = 0$ und

2. die zweite Ableitung der Gewinnfunktion kleiner oder gleich Null ist:

$G''=E''(x)-K''(x)\leqq0\!\,$

Somit ergibt sich aus der ersten Bedingung, dass 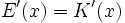$E^\prime(x)=K^\prime(x)$ gelten muss, was mit E(x) = px zu folgendem Ausdruck führt:

$K^\prime(x) = p$.

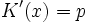Außerdem folgt aus der zweiten Bedingung mit E''(x) = 0, dass gelten muss:

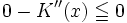$0-K''(x)\leqq0\!\,$    und daraus folgend    $K''(x)\geqq0\!\,$.

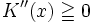Weil man in der Regel von mit steigender Produktionsmenge fallenden Grenzkosten auf Betriebsebene ausgehen muss, gilt für den einzelnen Anbieter aber immer:

$K''(x)<0\!\,$.

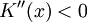Dies ist ein Widerspruch zur Maximums-Bedingung. Daraus folgt, dass es ein absolutes Gewinnmaximum für den Mengenanpasser nicht geben kann. Wichtigster Grund hierfür ist das Vorliegen von Skaleneffekten (siehe Grenzkosten). Ein Produzent kann seinen Gewinn bei gegebenem Preis immer dadurch vergrößern, dass er seine Produktion u.a. mithilfe der Ersetzung von Arbeit durch Kapital ausweitet (Gesetz der Massenproduktion).

(Mit G=Gewinn, E=Erlös, K=Kosten und den jeweiligen Ableitungen, p=Preis)