Gewinnmaximierung

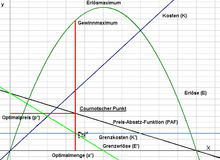
Gewinnmaximierung bezeichnet in der Neoklassischen Theorie den Mechanismus, nach dem in einer Marktwirtschaft Unternehmer ihre Produktionsmenge anpassen, damit ein Marktgleichgewicht erreicht wird. In der Situation maximalen Gewinns entsprechen die Grenzkosten dem Grenzerlös.

In der Betriebswirtschaftslehre gilt Gewinnmaximierung als ein wichtiges Unternehmensziel; doch genauer spricht Wilhelm Rieger hier von der Maximierung der Rentabilität des Eigenkapitals einer Unternehmung.^[1]

Formeln zur Gewinnmaximierung

Der Gewinn ist die Differenz zwischen dem Erlös und den Kosten, d.h. G = E - K. Das Gewinnmaximum liegt in dem Punkt, an dem der Grenzerlös E′ gleich den Grenzkosten K′ ist, also an dem E′ = K′ gilt. Aus G′ = E′ - K′ ergibt sich, dass der Grenzgewinn G′ an diesem Punkt 0 ist, d.h. G′ = 0 gilt. Formal könnte im Punkt G′ = 0 auch ein lokales Minimum vorliegen, die Bedingung G′ = 0 ist demnach notwendig, aber nicht hinreichend. Im Punkt G′ = 0 muss weiterhin G″ < 0 gelten (G″ ist die zweite Ableitung von G) um ein lokales Maximum formal zu garantieren (G′ = 0 und G″ < 0 ist eine hinreichende Bedingung für ein lokales Maximum).

Gewinnmaximum graphisch

Beispiel:

Gegeben sind die Preis-Absatz-Funktion

$p(x)=150- \frac {x} {20}$

und eine lineare Kostenfunktion

$K(x)=20000+30 \cdot x$

Daraus ergibt sich

$E(x)= p(x) \cdot x = 150 \cdot x - \frac {x^2} {20}$

$E'(x)= 150 - \frac {x} {10}$

$G(x) = E(x) - K(x) = \left(150 \cdot x - \frac {x^2} {20}\right) - (20000 + 30 \cdot x)$

$G'(x) = 150 - \frac {x} {10} - 30 = 120 - \frac {x} {10}$

$G'(x) = 120 - \frac {x} {10} = 0 \quad\Rightarrow\quad 1200 - x = 0 \quad\Rightarrow\quad 1200 = x$

$G(1200) = \left(150 \cdot 1200 - \frac {1200^2} {20}\right) - (20000 + 30 \cdot 1200) = 52000$

$p(1200) = 150 - \frac {1200} {20} = 90$

Bei 1.200 Mengeneinheiten ist das Gewinnmaximum in der Höhe von 52.000 Geldeinheiten erreicht. Der Preis pro Mengeneinheit beträgt dabei 90 Geldeinheiten.

Die Bedingung, dass G″ < 0 ist, ist in diesem Fall immer erfüllt, da

$G''(x) = - \frac {1} {10} \quad\Rightarrow\quad G'' < 0$ für alle $x \in \Re$

Anmerkungen

1. ↑ Wilhelm Rieger, Einführung in die Privatwirtschaftslehre, Nürnberg ³1984, ISBN 3-7896-0063-6

Siehe auch

• Formelsammlung Betriebswirtschaftslehre
• Formelsammlung Mikroökonomie