Mercator-Projektion

klassische Mercator-Projektion in normaler Lage

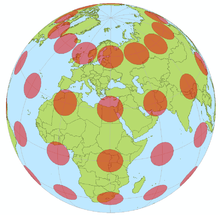
Die in der Kartografie verwendete Mercatorprojektion ist eine Form der Zylinderprojektion, bei der die Projektion in Richtung der Zylinderachse geeignet verzerrt ist, um eine winkeltreue Abbildung der Erdoberfläche zu erreichen. Die Mercatorprojektion ist dadurch eine unechte Projektion, die nicht geometrisch konstruiert werden kann. Die Winkeltreue ist gleichbedeutend mit Konformität, so dass geometrische Formen im Kleinen unverzerrt bleiben. Dagegen ist die Mercatorprojektion weder flächentreu noch richtungstreu, d.h. Flächeninhalte haben an verschiedenen Stellen der Abbildung unterschiedliche Maßstäbe und Großkreise als kürzeste Verbindungen zweier Punkte werden nicht gerade dargestellt. Längentreue besteht nur entlang einer oder zweier ausgezeichneter Linien. Nach der Lage der Achse des Projektionszylinders zur Erdachse unterscheidet man die normale Mercatorprojektion, bei der beide Achsen identisch sind, transversale Mercatorprojektionen mit Zylinderachsen senkrecht zur Erdachse sowie schiefe Mercatorprojektionen in den anderen Fällen.

erste Mercatorprojektion von 1569

Mercatorprojektionen finden insbesondere im Vermessungswesen und in der Navigation Anwendung, im Vermessungswesen überwiegend als transversale Projektionen mit unterschiedlichen Achsen für verschiedene Meridianstreifen (UTM, Gauß-Krüger-Projektion u.a.), in der Navigation als normale Projektion. Benannt ist die Mercatorprojektion nach dem Kartografen Gerhard Mercator, der zu Navigationszwecken 1569 eine Karte dieser Art in normaler Lage der Abbildungsfläche veröffentlichte, auf der erstmals ein gesteuerter Kurs als Gerade eingezeichnet werden konnte.

Verbreitung

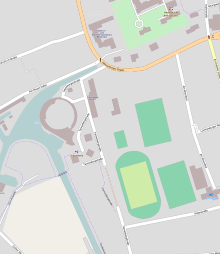Kreise bleiben Kreise, Quadrate bleiben Quadrate: Die Formentreue von Mercator - hier bei OpenStreetMap.

Die Erdoberfläche ist in erster Näherung eine Kugeloberfläche, die nicht verzerrungsfrei auf eine ebene Karte abgebildet werden kann. Auch im Internet nutzen sowohl freie Projekte wie OpenStreetMap als auch kommerzielle Anbieter wie Google Maps, Bing Maps und Yahoo Maps für zweidimensionale Darstellungen vorzugsweise diese Projektion.^[1].

Konstruktion

Um die Erde wird ein gedachter Zylinder gelegt, der diese entlang eines Großkreises berührt oder in zwei Kreisen beiderseits dieses Großkreises schneidet. Von der Zylinderachse aus kann jeder Punkt des Globus geometrisch auf eine Linie projiziert werden, die senkrecht zu diesem Großkreis liegt. Dabei werden innerhalb des Zylinders liegende Urbilder in Umfangsrichtung um so stärker vergrößert, je näher sie an der Achse liegen, außerhalb liegende werden verkleinert. Um Winkeltreue zu erreichen, muss ein solches Flächenelement daher in Achsrichtung um denselben Faktor vergrößert werden. Um die Lage in Achsrichtung zu bestimmen, muss die Vergrößerung über die Strecke von der Berührungslinie bis zum zu projizierenden Punkt rechnerisch integriert werden.

Normale Mercatorprojektion

Zylinderprojektion, normale Lage

Normale Mercator-Projektion

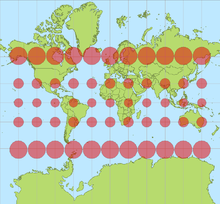
Bei der normalen Mercatorprojektion werden Breitenkreise und Meridiane zu Geraden. Flächen werden durch die Projektion auf die nun parallelen Meridiane in Ost-West-Richtung mit dem Kehrwert des Cosinus der geographischen Breite gedehnt. In Nord-Süd-Richtung muss daher dieselbe Dehnung vorgenommen werden, die Lage eines Punkte errechnet sich dann mit dem Integral des Kehrwerts des Cosinus der geographischen Breite.

Abbildungsgleichungen für normale Lage

Die folgenden Gleichungssysteme bestimmen die Koordinaten x und y eines Punktes auf einer Mercatorkarte aus seiner geographischen Breite φ und geographischen Länge λ (mit λ₀ als geographischer Länge des Kartenzentrums). Die Erde wird als kugelförmig angenommen; Längen sind mit dem Erdradius dimensionslos gemacht. Die Gleichung für y ist das oben genannte Integral des Kehrwerts des Cosinus der geographischen Breite (anstelle des Tangens bei der gnomonischen Zylinderprojektion):

$\begin{align} x &= \lambda - \lambda_0 \\ y &= \ln \left[ \tan \left( \frac {1} {4} \pi + \frac {1} {2} \varphi \right) \right] \\ &= \ln \left( \tan \varphi + \sec \varphi \right) \\ &= \frac {1} {2} \ln \left( \frac {1 + \sin \varphi} {1 - \sin \varphi} \right)\\ &= \mathop{\rm artanh} \left(\sin \varphi \right) \\ &= \mathop{\rm arsinh} \left( \tan \varphi \right) \end{align}$

Die Inverse ist die Gudermannfunktion:

$\begin{align} \varphi &= 2\arctan \left( e^y \right) - \frac{1} {2} \pi \\ &= \arctan \left( \sinh y \right) \\ &= \arcsin \left( \tanh y \right) \\ \lambda &= x + \lambda_0 \end{align}$

Transversale Mercatorprojektion

Die Anwendung der Mercatorprojektion in transversaler Lage des Abbildungszylinders wurde 1772 von Johann Heinrich Lambert veröffentlicht. Zur Steigerung der Genauigkeit erweiterte Carl Friedrich Gauß 1825 die Anwendung auf das Erdellipsoid, die von Louis Krüger 1912 für die praktische Anwendung weiter untersucht wurde.

Transversale Lage, Zylinder schneidet den Globus

Transversale Mercator-Projektion für 45°E

Transversale Mercator-Projektion für den Nullmeridian

Abbildungseigenschaften

Tissotsche Indikatrix des Globus in perspektivischer Darstellung

Tissotsche Indikatrix der Mercatorprojektion

Die wichtigste Eigenschaft der Mercatorprojektion ist ihre Winkeltreue. Diese bedeutet auch, dass in kleinen Bereichen der Längenmaßstab in allen Richtungen gleich ist. Jedoch ist er nur entlang der Berührungslinie und ihrer Parallelen konstant. Nur an Berührungslinien ist die Projektion längentreu, d.h. entspricht dem angegebenen Maßstab. Damit ist sie auch nicht flächentreu. Die Verzerrungen werden mit Abstand zur Berührungslinie zunehmend größer und an der Achse der Projektion unendlich. Bei zwei Berührungslinien wird der Bereich zwischen diesen gestaucht.

Eine zusätzliche wichtige Eigenschaft für die Mercatorprojektion in normaler Lage ist die Achsentreue. Das heißt hier, dass die Nordrichtung überall auf der Karte dieselbe ist. Zusammen mit der Winkeltreue bedeutet dies, dass Loxodromen (d.h. gleichbleibende Kurse) als Geraden abgebildet werden. Kürzeste Verbindungen entstehen dadurch jedoch nicht, dazu wäre stattdessen Richtungstreue erforderlich (→ gnomonische Azimutalprojektion). In normaler Lage werden zum Nord- und Südpol hin die Verzerrungen immer größer. Dadurch ist die Insel Grönland (2,2 Mio. km²) in dieser Kartenprojektion fast so groß dargestellt wie der Kontinent Afrika (30,3 Mio. km²). Der Nord- und der Südpol können nicht dargestellt werden, da der projizierte Punkt im Unendlichen liegen würde.

Nutzung

Die normale Mercator-Abbildung liegt wegen ihrer Winkel- und Achsentreue fast allen Seekarten und einigen Luftfahrtkarten zugrunde. Die Maßstabsänderungen sind auf größeren Ausschnitten der Erdoberfläche merklich, so dass die am Kartenrand gedruckte Breitengradskala nicht äquidistant ist. Eine Seemeile auf der Seekarte entspricht genau einer Bogenminute auf der gleichen Breite am linken oder rechten Kartenrand.

Für kleinräumige Karten, insbesondere für die Grundkarten sehr vieler Landesvermessungen, findet die transversale Mercatorprojektion in Form von Gauß-Krüger-Projektion, Universaler transversaler Mercatorprojektion (UTM) und ähnlichen in großem Umfang Anwendung. Die UTM findet Anwendung in 30 unterschiedlichen Achslagen für jeweils 6° breite Streifen, Gauß-Krüger verwendet doppelt so viele Lagen für Streifen von 3°. Um die Längentreue über die breitere Abbildungsfläche zu verbessern, schneidet bei der UTM der Projektionszylinder den Erdellipsoid in zwei Linien. In Deutschland und Österreich war bisher die Gauß-Krüger-Projektion Grundlage der Landesvermessung. Die in der Geodäsie mittlerweile erforderliche internationale Zusammenarbeit hat international der auf Gauß-Krüger basierenden jüngeren Universalen Transversalen Mercatorprojektion zur Durchsetzung verholfen, auf die auch in Deutschland und Österreich umgestellt wird.

In der schweizerischen Landesvermessung findet eine schiefachsige Mercatorprojektion Anwendung, bei der die Achse so gewählt ist, dass der Fundamentalpunkt der Landesvermessung, die Sternwarte Bern, auf demselben Meridian sowie auf der Berührungslinie liegt.^[2]

Für großflächige Karten, insbesondere Weltkarten, soweit sie nicht speziell der Kursbestimmung in der Navigation dienen, ist die Mercatorprojektion wegen ihrer mit zunehmendem Abstand von der Berührungslinie stark zunehmenden Verzerrungen ungeeignet. Dass sie hier dennoch zeit- und teilweise verwendet wurde, führte ab 1974 der zu einer vom Historiker Arno Peters initiierten Diskussion um die Mercatorprojektion und die vermeintliche Alternative der in der Kartographie als Galls orthographische Projektion bekannten flächentreuen zylindrischen Peters-Projektion. Peters kritisierte, dass die Mercatorprojektion ein „eurozentrisches Weltbild“ vermittele, da auf einer Weltkarte in normaler Mercatorprojektion Länder in gemäßigten Breiten wie Europa und andere Industrieländer im Verhältnis größer erscheinen als äquatornahe Gebiete, wo hauptsächlich Entwicklungsländer liegen.

Nachweise

1. ↑ Frederik Ramm, Jochen Topf: OpenStreetMap: Die freie Weltkarte nutzen und mitgestalten, ISBN 978-3-86541-375-8
2. ↑ Schweizerisches Bundesamt für Landestopographie, Website: Schweizerische Kartenprojektionen

Literatur

• Mark Monmonier: Rhumb Lines and Map Wars: A Social History of the Mercator Projection. University of Chicago Press, Chicago 2004, ISBN 0226534316.
• Reinhard Buchholz, Wilhelm Krücken: Die Mercator-Projektion. Zu Ehren von Gerhard Mercator (1512–1594). Becker, Velten 1994 ISBN 3-930640-36-8.

Weblinks

• Ad maiorem Gerardi Mercatoris gloriam Umfangreiche Website von F. Wilhelm Krücken zu Mercator und der mathematischen Entwicklung des nach ihm benannten Kartennetzentwurfs. Dazu eine ausführliche Auseinandersetzung mit der Peters-Projektion.