Archimedisches Axiom

Das sogenannte archimedische Axiom ist nach dem antiken Mathematiker Archimedes benannt, es ist aber älter und wurde schon von Eudoxos von Knidos in seiner Größenlehre formuliert.^[1] In moderner Präzisierung lautet es folgendermaßen:

Zu je zwei Größen y > x > 0 existiert eine natürliche Zahl $n\in \mathbb{N}$ mit nx > y.

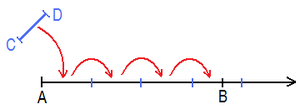
Geometrisch lässt sich das Axiom derart interpretieren: Hat man zwei Strecken auf einer Geraden, so kann man die größere von beiden übertreffen, wenn man die kleinere nur oft genug abträgt.

Eine (an)geordnete Gruppe oder ein (an)geordneter Körper, in welchem das Archimedische Axiom gilt, heißt archimedisch (an)geordnet.

Für den Körper $\mathbb{R}$ der reellen Zahlen wird es manchmal axiomatisch eingeführt. Man kann allerdings mit den Axiomen eines geordneten Körpers und dem Supremumsaxiom (Jede nach oben beschränkte Teilmenge des Körpers besitzt ein Supremum) beweisen, dass die reellen Zahlen archimedisch geordnet sind.

zur geometrischen Interpretation

Beweis aus dem Supremumsaxiom für einen geordneten Körper

Es sei x > 0.

Behauptung: Für jedes y > x gibt es eine natürliche Zahl n, so dass nx > y gilt.

Gegenannahme: Es gibt ein y > 0, so dass $nx\leq y$ für alle natürlichen Zahlen n.

Dann ist y eine obere Schranke für nx. Aus dem Supremumsaxiom folgt die Existenz einer kleinsten oberen Schranke y₀. Dann ist aber auch y₀ − x eine obere Schranke (wenn $nx\leq y_0$ für alle natürlichen Zahlen n, so gilt sicher auch $nx\leq y_0-x$ für alle natürlichen Zahlen n). Wegen y₀ − x < y₀, ist y₀ keine kleinste obere Schranke. Dies ist ein Widerspruch. Also muss die Gegenannahme falsch sein und die Behauptung ist bewiesen.

Folgerungen aus dem archimedischen Axiom

Zu jeder Zahl $x\in\mathbb{R}$ gibt es $n_1,n_2\in\mathbb{N}$, so dass n₁ > x und − n₂ < x. Daraus folgt: Zu jedem $x\in\mathbb{R}$ gibt es eine eindeutig bestimmte Zahl $n\in\mathbb{Z}$ mit

$n\leq x < n+1.$

Dabei wird n mit $\lfloor x\rfloor$ oder $\operatorname{floor}(x)$ bezeichnet. Ebenso existiert eine eindeutig bestimmte Zahl $m\in\mathbb{Z}$ mit

$m-1 < x \leq m$

welche mit $\lceil x\rceil$ oder $\operatorname{ceil}(x)$ bezeichnet wird. Damit gilt auch: für alle ε > 0 existiert ein $n \in \mathbb{N}$ mit $n>1/\epsilon$ und daher umgekehrt $1/n<\epsilon$. In der Analysis ist dieser Zusammenhang nützlich, um beispielsweise die Konvergenz oder Divergenz von Folgen nachzuweisen.

Weiterhin folgt aus dem archimedischen Axiom, dass es für zwei reelle Zahlen $a,b\in\mathbb{R}, a < b$ immer eine rationale Zahl $q\in\mathbb{Q}$ mit a < q < b gibt.

Satz von Hölder

Jede archimedisch geordnete Gruppe G ist kommutativ und isomorph zu einer additiv geordneten Untergruppe von $\R$.

Dabei ist für ein $e \in G$ mit e > 0 und additiv geschriebener Gruppenverknüpfung die Abbildung

$x \mapsto r = \sup\, \{ \frac {z}{n} |z \in \Z, n \in \N, z \cdot e < n \cdot x \}$

ein Isomophismus von G in eine additive geordnete Untergruppe von $\R$, wobei $n \cdot x = \underbrace {x+x+...+x}_{n-mal}$ für $x \in G$ und $n \in N$ und $z\cdot e = -z \cdot (-e)$ für $z \in Z$ und z < 0.^[2]

Das Element e kann dabei als Einheit verwendet werden, mit dem jedes Gruppenelement x "gemessen" werden kann. Das bedeutet: Für jedes Element x der Gruppe existiert ein r so, dass $x = r \cdot e ( r \in \R)$.

Beispiel: Die Intervalle in der Musiktheorie bilden eine archimedisch geordnete kommutative Gruppe und können alle mit der Einheit Oktave oder Cent gemessen werden.

Klassifizierung: Entweder ist eine archimedisch geordnete Gruppe G von der Form G = {..., −3a, −2a, −a, 0, a, 2a, 3a, ...} oder:

Zu jedem Element a>0 gibt es ein b mit 0 < 2b < a. (Gibt es nämlich kein minimales positives a, dann gibt es zu jedem a > 0 sicher ein c mit 0 < c < a. Falls 2c < a kann man b = c wählen. Falls 2c = a gibt es ein b mit 0 < 2b < 2c =a und falls 2c > a gilt für b = a − c die Ungleichung 0 < 2b = 2a − 2c < 2a − a = a.)

Nichtarchimedisch angeordnete Körper

Ein Beispiel für einen angeordneten Körper, in dem das Axiom des Archimedes nicht gilt, ist der in der Nichtstandardanalysis studierte Körper der hyperreellen Zahlen.

Ein einfacheres Beispiel besteht aus den rationalen Funktionen R(x) über dem rationalen (oder dem reellen) Zahlenkörper, die so geordnet werden, dass x größer ist als alle Zahlen (das geht auf eindeutige Weise).

Referenzen

1. ↑ überliefert in: Euklid, Elemente V, Definition 4: Dass sie ein Verhältnis zueinander haben, sagt man von Größen, die vervielfältigt einander übertreffen.
2. ↑ Alexander Gennadjewitsch Kurosch Vorlesungen über Allgemeine Algebra. Harri Deutsch, Zürich 1964.