Mittag-Leffler-Theorem

Der Satz von Mittag-Leffler ist ein nach dem Mathematiker Magnus Gösta Mittag-Leffler benannter Satz der Funktionentheorie. In seiner anwendungsorientierten Formulierung garantiert er die Existenz bestimmter meromorpher Funktionen.

Satz

Zu einer diskreten Folge (p_n) verschiedender komplexer Zahlen existiert eine auf 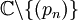$\mathbb{C} \backslash \{(p_n)\}$ holomorphe Funktion, die ihre Polstellen genau in den p_n, $n\in\mathbb{N}$ hat und dort jeweils einen vorgegebenen Hauptteil aufweist. 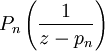Das heißt, zu jedem dieser p_n kann man ein Polynom P_n(z) ohne konstanten Term wählen, nach dem Satz von Mittag-Leffler existiert eine meromorphe Funktion, deren Laurententwicklung auf einer gelochten Kreisscheibe um p_n gerade den Hauptteil $P_n\left(\frac{1}{z-p_n}\right)$ besitzt.

Bemerkungen

• Mit der Wahl eines Polynoms an einer Polstelle legt man gleichzeitig die Ordnung des Pols fest, sie ist gleich dem Grad des Polynoms.
• Ist die Polstellenmenge endlich, so konvergiert die Summe der Hauptteile trivialerweise.
• Wenn die Polstellenmenge unendlich ist, kann man im Allgemeinen nicht davon ausgehen, dass die Summe der Hauptteile konvergiert. In diesem Fall werden sogenannte konvergenzverbessernde Summanden für jeden Hauptteil eingeführt. In den meisten Fällen sind dies Taylorpolynome, die den Hauptteil nicht verändern, sondern nur den entsprechenden Nebenteil der Laurententwicklung.

Beispiele

In einem einfachen Beispiel erhält man die Partialbruchzerlegung einer Funktion. Betrachte f(x) = π² / (sin(πx))². f besitzt genau an den ganzen Zahlen Pole zweiter Ordnung. Der Ansatz, als Polynome einfach x² und somit für die Hauptteile in 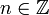$n \in \mathbb Z$ gerade den Term 1 / (z − n)² zu wählen, führt zu 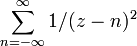$\sum_{n=-\infty}^{\infty} 1/(z-n)^2$. Es lässt sich zeigen, dass diese Summe schon konvergiert und gleich f ist. Insbesondere werden keine konvergenzverbessernden Summanden benötigt.

Verallgemeinerung

An Stelle von Polynomen können auch ganze Funktionen gewählt werden, also Potenzreihen ohne konstanten Term, die auf ganz $\mathbb C$ konvergieren. Damit hat die resultierende Funktion aber wesentliche Singularitäten und ist nicht mehr meromorph.

Literatur

• E. Freitag, R. Busam: Funktionentheorie 1. Springer, 2006, ISBN 3540317643. 
• Klaus Jänich: Funktionentheorie. 6 Auflage. Springer, 2004, ISBN 3540203923.