Modularer Verband

Hassediagramm von N₅, dem kleinsten nichtmodularen Verband.

Ein modularer Verband im Sinne der Ordnungstheorie ist ein Verband, der die folgende selbst-duale Bedingung erfüllt (Modularitätsgesetz):

$x \leq b$ impliziert $x \vee(a \wedge b) = (x \vee a) \wedge b.$

Modulare Verbände treten in der Algebra und vielen anderen Bereichen der Mathematik auf. So bilden beispielsweise die Unterräume eines Vektorraums (und allgemeiner die Untermoduln eines Moduls über einem Ring) einen modularen Verband.

Jeder distributive Verband ist modular.

In einem nichtmodularen Verband, kann es dennoch Elemente b geben, die das Modularitätsgesetz zusammen mit beliebigen Elementen a und x erfüllen (unter der Bedingung x ≤ b). Ein solches Element b heißt modulares Element. Noch allgemeiner kann man Paare (a, b) von Elementen betrachten, die das Modularitätsgesetz für alle Elemente x erfüllen. Ein solches Paar heißt modulares Paar, und es gibt mehrere mit der Semimodularität zusammenhängende Verallgemeinerungen von Modularität, die auf diesen Begriff aufbauen.

Einführung

Das Modularitätsgesetz kann man als ein eingeschränktes Assoziativgesetz auffassen, das die beiden Verbandsoperationen in ähnlicher Weise verknüpft wie das Assoziativgesetz λ(μx) = (λμ)x für Vektorräume die Körpermultiplikation mit der skalaren Multiplikation. Die Einschränkung x ≤ b ist nötig, da sie aus x ∨ (a ∧ b) = (x ∨ a) ∧ b folgt.

Nichtmodularität von N₅.

Man kann leicht überprüfen, dass aus x ≤ b in jedem Verband x ∨ (a ∧ b) ≤ (x ∨ a) ∧ b folgt. Daher kann man das Modularitätsgesetz auch wie folgt formulieren:

Modularitätsgesetz (Variante)

x ≤ b impliziert x ∨ (a ∧ b) ≥ (x ∨ a) ∧ b.

Indem man für x den Term x ∧ b einsetzt, kann man das Modularitätsgesetz wie folgt durch eine Gleichung ausdrücken, die ohne Vorbedingungen erfüllt sein muss:

(x ∧ b) ∨ (a ∧ b) = [(x ∧ b) ∨ a] ∧ b.

Das zeigt (unter Benutzung von Begriffen aus der universellen Algebra), dass die modularen Verbände eine Untervarietät der Varietät der Verbände bilden. Daher sind alle homomorphen Bilder, Unterverbände und direkten Produkte von modularen Verbänden wieder modular.

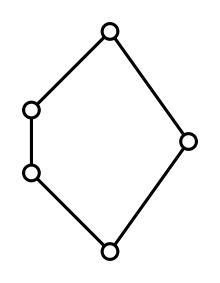
Der kleinste nichtmodulare Verband ist der "Pentagonverband" N₅, der aus fünf Elementen 0,1,x,a,b besteht, so dass 0 < x < b < 1, 0 < a < 1, und a nicht mit x oder mit b vergleichbar ist. Für diesen Verband gilt x ∨ (a ∧ b) = x ∨ 0 = x < b = 1 ∧ b = (x ∨ a) ∧ b, im Widerspruch zum Modularitätsgesetz. Jeder nichtmodulare Verband hat eine Kopie von N₅ als Unterverband.

Nach Richard Dedekind, der das Modularitätsgesetz entdeckte, werden modulare Verbände manchmal heute noch als Dedekindverbände bezeichnet.

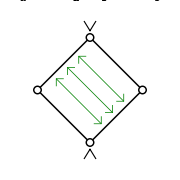
Diamant-Isomorphiesatz

Für je zwei Elemente a,b eines modularen Verbandes kann man die Intervalle [a ∧ b, b] und [a, a ∨ b] betrachten. Zwischen ihnen gibt es die ordnungserhaltenden Abbildungen

φ: [a ∧ b, b] → [a, a ∨ b] und

ψ: [a, a ∨ b] → [a ∧ b, b],

definiert durch φ(x) = x ∨ a und ψ(x) = x ∧ b.

• 

  In einem modularen Verband sind die angedeuteten Abbildungen φ and ψ Isomorphismen und invers zu einander.

• 

  Gegenbeispiel zum Diamant-Isomorphiesatz in einem nichtmodularen Verband.

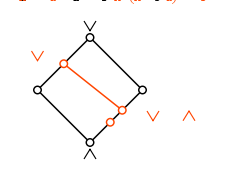
Die Zusammensetzung ψφ ist eine ordnungserhaltende Abbildung vom Intervall [a ∧ b, b] in sich selbst, die außerdem die Ungleichung ψ(φ(x)) = (x ∨ a) ∧ b ≥ x erfüllt. Das Beispiel zeigt, dass diese Ungleichung i.A. keine Gleichung sein muss. In einem modularen Verband gilt dagegen immer die Gleichung. Da der duale Verband zu einem modularen Verband wieder dual ist, ist φψ ebenso die Identitätsabbildung auf [a, a ∨ b]; daher sind φ und ψ Isomorphismen zwischen diesen beiden Intervallen. Dieses Ergebnis wird manchmal als Diamant-Isomorphiesatz für modulare Verbände bezeichnet. Ein Verband ist genau dann modular, wenn der Diamant-Isomorphiesatz für jedes Paar von Elementen gilt.

Der Diamant-Isomorphiesatz für modulare Verbände ist analog zum dritten Isomorphiesatz in der Algebra, und er ist eine Verallgemeinerung des Verbandssatzes.

Modulare Paare

Der mit einem Mittelpunkt versehene Hexagonverband S₇, auch als D₂ bekannt, ist M-symmetrisch aber nicht modular.

In jedem Verband versteht man unter einem modularen Paar ein Paar (a, b) von Elemente, so dass für alle Elemente x, die a ∧ b ≤ x ≤ b erfüllen, die Gleichung (x ∨ a) ∧ b = x gilt. In anderen Worten sind die modularen Paare die Paare, für welche die eine Hälfte des Diamant-Isomorphiesatzes gilt. Der französische Ausdruck für "modulares Paar" ist couple modulaire. Ein Paar (a, b) heißt auf französisch paire modulaire, falls sowohl (a, b) als auch (b, a) modulare Paare sind. Ein Verbandselement b heißt (rechts-) modulares Element falls für alle Elemente a das Paar (a, b) modular ist.

Manche Verbände haben die Eigenschaft dass für jedes modulare Paar (a, b) auch das Paar (b, a) modular ist. Ein solcher Verband heißt M-symmetrischer Verband. Einige Autoren, zum Beispiel Fofanova, bezeichnen solche Verbände als semimodulare Verbände. Da jeder M-symmetrische Verband semimodular ist und für Verbände von endlicher Länge auch die Umkehrung gilt, kann dies nur für gewisse unendliche Verbände zu Verwirrung führen. Da ein Verband genau dann modular ist, wenn jedes Paar von Elementen modular ist, ist jeder modulare Verband M-symmetrisch. Im oben beschriebenen Verband N₅ ist das Paar (b, a) modular, nicht aber das Paar (a, b). Folglich ist N₅ nicht M-symmetrisch. Der mit einem Mittelpunkt versehene Hexagonverband S₇ ist M-symmetrisch, aber nicht modular. Da N₅ ein Unterverband von S₇ ist, bilden die M-symmetrischen Verbände keine Untervarietät der Varietät der Verbände.

M-Symmetrie ist kein selbstdualer Begriff. Ein dual-modulares Paar ist ein Paar, welches im dualen Verband modular ist, und ein Verband heißt dual M-symmetrisch oder M^*-symmetrisch falls der duale Verband M-symmetrisch ist. Man kann zeigen, dass ein endlicher Verband genau dann modular ist, wenn er M-symmetrisch und M^*-symmetrisch ist. Dieselbe Äquivalenz gilt für unendliche Verbände, welche die aufsteigende Kettenbedingung (oder die absteigende Kettenbedingung) erfüllen.

Einige weniger wichtige Begriffe stehen im engen Zusammenhang hierzu. Ein Verband heißt kreuzsymmetrisch, falls für jedes modulare Paar (a, b) das Paar (b, a) dual modular ist. Aus Kreuzsymmetrie folgt M-Symmetrie, aber nicht M^*-Symmetrie. Daher ist Kreuzsymmetrie nicht zur dualen Kreuzsymmetrie äquivalent. Ein Verband mit einem kleinsten Element 0 heißt ⊥-symmetrisch falls für jedes modulare Paar (a, b), welches a ∧ b = 0 erfüllt, das Paar (b, a) ebenfalls modular ist.

Literatur

• Richard Dedekind (1897), "Ueber Zerlegungen von Zahlen durch ihre grössten gemeinsamen Teiler", Braunschweiger Festschrift: 1–40
• T. S. Fofanova (2001): "Semi-modular lattice", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
• Maeda, Shûichirô (1965): "On the symmetry of the modular relation in atomic lattices", Journal of Science of the Hiroshima University 29: 165–170
• L. A. Skornyakov (2001): "Modular lattice", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
• Manfred Stern (1999): Semimodular lattices, Cambridge University Press, ISBN 978-0-521-46105-4
• George Grätzer (1998): General Lattice Theory (2. Auflage), Birkhauser, ISBN 978-0817652395

Weblinks

• Modular lattice bei Planet Math