Modulgruppe

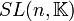Lineare Gruppen dienen in der Mathematik der Beschreibung kontinuierlicher Symmetrien. Die spezielle lineare Gruppe vom Grad n über einem Körper $\mathbb{K}$ (oder allgemeiner einem kommutativen, unitären Ring), $SL(n, \mathbb{K} )$, ist die Gruppe aller n×n Matrizen mit Koeffizienten aus $\mathbb{K}$, deren Determinante 1 beträgt. Gruppenverknüpfung ist die Matrizenmultiplikation.

Wenn aus dem Kontext klar ist, dass der Körper die Menge $\mathbb{R}$ der reellen oder $\mathbb{C}$ der komplexen Zahlen ist, schreibt man auch SL(n).

Eigenschaften

Die spezielle lineare Gruppe 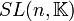$SL(n,\mathbb{K} )$ ist eine normale Untergruppe der allgemeinen linearen Gruppe $GL(n, \mathbb{K})$.

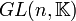Die Faktorgruppe 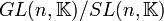$GL(n,\mathbb{K})/SL(n, \mathbb{K})$ ist isomorph zu $\mathbb{K}$^×, der multiplikativen Gruppe von $\mathbb{K}$ (für einen Körper $\mathbb{K}$ ist $\mathbb{K}$^× gleich $\mathbb{K}$ ohne die 0).

Wichtige Untergruppen der 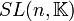$SL(n,\mathbb{K})$ sind die spezielle orthogonale Gruppe SO(n, $\mathbb{K}$) und die spezielle unitäre Gruppe $SU(n,\mathbb{K})$.

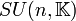Die spezielle lineare Gruppe SL(n) über dem Körper $\mathbb{R}$ oder $\mathbb{C}$ ist eine Lie-Gruppe über $\mathbb{K}$ der Dimension n²-1.

Die speziellen linearen Gruppen sind algebraische Gruppen, da die Bedingung, dass die Determinante gleich 1 sein muss, durch eine polynomiale Gleichung in den Matrix-Koeffizienten ausgedrückt werden kann.

Die spezielle lineare Gruppe 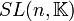$SL(n,\mathbb{K})$ beinhaltet alle orientierungstreuen und volumenerhaltenden linearen Abbildungen.

Siehe auch

• Modulform