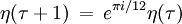Dedekindsche Eta-Funktion
- Dedekindsche Eta-Funktion
-

Die Dedekindsche η-Funktion in der komplexen Ebene
Die nach dem deutschen Mathematiker Richard Dedekind benannte η-Funktion ist eine auf der oberen Halbebene 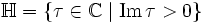 holomorphe Funktion.
holomorphe Funktion.
Sie spielt eine wichtige Rolle in der Theorie der elliptischen Funktionen und der Thetafunktionen.
Definition
Die η-Funktion wird üblicherweise folgendermaßen als unendliches Produkt definiert:
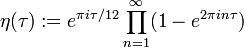 .
.
Aus der Definition folgt unmittelbar, dass η in 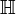 keine Nullstellen hat.
keine Nullstellen hat.
Die η-Funktion ist eng verwandt mit der Diskriminante Δ, es ist
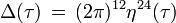 .
.
Zur Berechnung der η-Funktion kann der Pentagonalzahlensatz verwendet werden.
Transformationsverhalten
Ihre Bedeutung erhält die η-Funktion aus ihrem Transformationsverhalten unter den Substitutionen der Erzeugenden der Modulgruppe
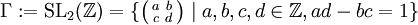 ,
,
es gilt nämlich:
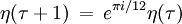
und
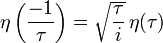 .
.
Literatur
- Tom M. Apostol: Modular Functions and Dirichlet Series in Number Theory, Springer-Verlag, Berlin Heidelberg New York (1990), ISBN 3-540-97127-0
- Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Aufl., Springer-Verlag, Berlin (2006), ISBN 3-540-31764-3
- Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen, 2. Aufl., Springer-Verlag, Berlin (2007), ISBN 978-3-540-49324-2
Weblinks
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Dedekindsche η-Funktion — Die Dedekindsche η Funktion in der komplexen Ebene Die nach dem deutschen Mathematiker Richard Dedekind benannte η Funktion ist eine auf der oberen Halbebene holomorphe Funktion. Sie spielt eine wichtige Rolle in der Theor … Deutsch Wikipedia
Eta-Funktion — Als Eta Funktion oder η Funktion werden in der Mathematik folgende Funktionen bezeichnet: Dedekindsche η Funktion, nach dem Mathematiker Dedekind Dirichletsche Eta Funktion, nach dem Mathematiker Dirichlet Diese Seite ist eine … Deutsch Wikipedia
Dirichletsche Eta-Funktion — Die dirichletsche η Funktion in der komplexen Zahlenebene. In der Zahlentheorie ist die dirichletsche η Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805−1859) benannt ist. Sie ist verwandt mit der … Deutsch Wikipedia
Dirichlet'sche Eta-Funktion — Die dirichletsche η Funktion in der komplexen Zahlenebene. In der Zahlentheorie ist die dirichletsche η Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805−1859) benannt ist. Sie ist verwandt mit der … Deutsch Wikipedia
ETA — ist: ein weiblicher Vorname Eta (Majuskel Η, Minuskel η) der 7. Buchstabe des griechischen Alphabets eine alte Bezeichnung für einen bestimmten Teil der Buraku, einer japanische Minderheitengruppe ein griechischer Buchstabe, der in der Technik… … Deutsch Wikipedia
Dedekindsche Funktion — In der Zahlentheorie werden mehrere Funktionen nach Richard Dedekind benannt: Dedekindsche Zeta Funktion Dedekindsche Eta Funktion Dedekindsche Psi Funktion Diese Seite ist eine Begriffsklärung z … Deutsch Wikipedia
Eta — Aussprache antik [ɛː] modern [i] Entsprechungen lateinisch H kyrillisch И h … Deutsch Wikipedia
Dedekind-Funktion — In der Zahlentheorie werden mehrere Funktionen nach Richard Dedekind benannt: Dedekindsche Zeta Funktion Dedekindsche Eta Funktion Dedekindsche Psi Funktion … Deutsch Wikipedia
Heta/eta — Eta Aussprache antik [ɛː] modern [i] Entsprechungen lateinisch H … Deutsch Wikipedia
Dirichlet'sche η-Funktion — Die dirichletsche η Funktion in der komplexen Zahlenebene. In der Zahlentheorie ist die dirichletsche η Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805−1859) benannt ist. Sie ist verwandt mit der … Deutsch Wikipedia
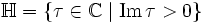 holomorphe Funktion.
holomorphe Funktion.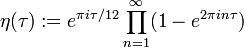 .
.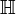 keine Nullstellen hat.
keine Nullstellen hat.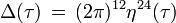 .
.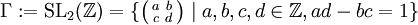 ,
,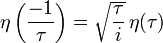 .
.