Arithmetische Codierung

Das arithmetische Kodieren wird unter anderem zur verlustfreien Datenkompression eingesetzt und ist eine Form der Entropiekodierung.

Dieser Artikel beschreibt nur, wie man mit einem gegebenen Satz von Zeichen-Wahrscheinlichkeits-Paaren einzelne Zeichen kodieren kann, welche eine möglichst kleine mittlere Wortlänge benötigt. Dabei ist durch die Entropie (mittlerer Informationsgehalt) eine untere Schranke gegeben (Quellencodierungstheorem).

Da zu einem Entropiekodierer immer auch ein Modell gehört, sollten die zusätzlichen Informationen aus dem Artikel zur Entropiekodierung entnommen werden.

Grundprinzip

Das Verfahren funktioniert theoretisch mit unendlich genauen reellen Zahlen, auch wenn in den eigentlichen Implementierungen dann wieder auf endlich genaue Integer- oder Gleitkommazahlen zurückgegriffen werden muss. Dies führt aber immer dazu, dass gerundet werden muss und somit das Ergebnis nicht mehr optimal ist.

Die Eingaben für den Arithmetischen Kodierer werden im Folgenden als Zeichen oder Symbole bezeichnet. Die Ausgabe für den Kodierer ist eine reelle Zahl (hier mit x bezeichnet).

Zuerst müssen sich Kodierer und Dekodierer auf ein Intervall einigen, in dem sich die Zahl x befinden soll. Normalerweise wird hier der Bereich zwischen 0 und 1 (exklusive) benutzt, also $[0, 1) := \{x \in \mathbb{R} \,|\, 0 \le x < 1\}$.

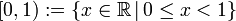Außerdem müssen Kodierer und Dekodierer bei der De- bzw. Kodierung eines Zeichens immer identische Tabellen mit den Wahrscheinlichkeiten aller möglichen dekodierbaren Zeichen zur Verfügung haben. Für die Bereitstellung dieser Wahrscheinlichkeiten ist das Modell verantwortlich.

Eine Möglichkeit ist, vor dem Kodieren speziell für die Eingabedaten eine Häufigkeitsanalyse zu erstellen und diese dem Dekodierer, zusätzlich zur eigentlichen Nachricht, mitzuteilen. Kodierer und Dekodierer verwenden dann für alle Zeichen diese Tabelle.

Zunächst zum Kodierer:

1. Initialisiere das aktuelle Intervall mit dem vereinbarten Startintervall (meistens 0 bis 1 exklusive).
2. Zerlege das aktuelle Intervall auf die identische Art wie der Dekodierer in Subintervalle, und weise jedem Subintervall ein Zeichen zu (siehe oben).
3. Das Subintervall, das dem nächsten Zeichen der Eingabe entspricht, wird zum aktuellen Intervall.
4. Sind noch weitere Zeichen zu kodieren, dann weiter bei Punkt 2. Sonst weiter beim nächsten Punkt.
5. Gib eine beliebige Zahl aus dem aktuellen Intervall und zusätzlich die Anzahl der kodierten Zeichen aus. Dieses ist die Zahl x, die vom Dekodierer wie oben beschrieben entschlüsselt werden kann. Diese Zahl wird so gewählt, dass sie möglichst wenig Nachkommastellen hat, also möglichst "rund" ist und sich daher mit relativ wenigen Bits darstellen lässt.

Nun der Dekodierer:

Der Dekodierer kann nun ein Zeichen nach dem anderen entschlüsseln, indem er folgende Schritte ausführt:

1. Initialisiere das aktuelle Intervall mit dem vereinbarten Intervall (meistens 0 bis 1 exklusive)
2. Unterteile das aktuelle Intervall in Subintervalle, wobei jedem kodierbaren Zeichen ein Subintervall zugewiesen wird. Die Größe der Subintervalle wird von der Häufigkeit des Auftretens des Zeichens bestimmt (Auftretenswahrscheinlichkeit). Die Reihenfolge der Intervalle ist durch eine Vereinbarung festgelegt (z. B. in alphabetischer Ordnung).
3. Finde heraus, in welchem dieser Subintervalle die Zahl x liegt und gib das Zeichen aus, das diesem Subintervall zugeordnet ist. Außerdem wird dieses Subintervall nun zum aktuellen Intervall.
4. Sind noch weitere Zeichen zu dekodieren, fahre fort bei Punkt 2, mit dem neuen aktuellen Intervall.

Bei diesem Algorithmus fällt auf, dass er nicht terminiert: Es ist allein an der Zahl x nicht erkennbar, wann das letzte Zeichen dekodiert wurde. Es muss dem Dekodierer also immer durch eine zusätzliche Information mitgeteilt werden, wann er seine Arbeit beendet hat. Dies wird üblicherweise in Form einer Längenangabe realisiert, kann aber auch (bspw. wenn bei der Kodierung nur ein einziger Datendurchlauf erwünscht ist) durch ein Sonderzeichen mit der Bedeutung „Ende“ geschehen.

Die Intervallteilung

Die Subintervalle müssen so gewählt werden, dass Kodierer und Decodierer die Größe und Position gleich bestimmen. Wie oben schon erwähnt, ergibt sich die Größe der Subintervalle aus den Wahrscheinlichkeiten der Zeichen.

Die Anordnung (Reihenfolge) der Intervalle dagegen ist für die Qualität des Algorithmus nicht von Bedeutung, sodass man hier eine beliebige Reihenfolge fest vorgeben kann. Diese ist Gegenstand einer Vereinbarung (z. B. alphabetische Ordnung).

Eine Möglichkeit für die Berechnung der Intervalle ist folgende:

$\begin{matrix} I_l(n+1)&=&I_l(n)+I_s L\\ I_h(n+1)&=&I_l(n)+I_s H \end{matrix}$

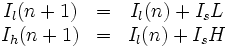
I_l und I_h sind die Grenzen des Intervalls. I_s ist die Größe des Intervalls, also I_h − I_l. Die beiden Werte L und H sind die Summe der Wahrscheinlichkeiten aller Zeichen mit einem Code kleiner, bzw. kleiner gleich dem zu kodierenden Zeichen x.

$\begin{matrix} L&=&\sum p(i), i < x\\ H&=&\sum p(i), i \le x \end{matrix}$

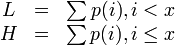
Beispiel

Intervallschachtelung beim Arithmetischen Kodieren

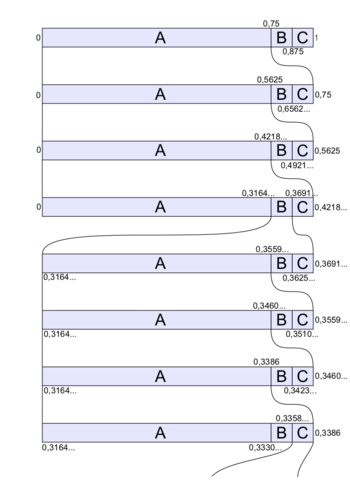
In diesem Beispiel wird die Zeichenkette "AAABAAAC" komprimiert. Zuerst wird für die Größe der Subintervalle die Häufigkeiten aller Zeichen benötigt. Der Einfachheit halber wird eine statische Wahrscheinlichkeit für alle Zeichen verwendet.

Zeichen	Häufigkeit	optimale Bitzahl
p(A)	75%	0,415
p(B)	12,5%	3
p(C)	12,5%	3

Die optimale Bitzahl ergibt sich aus der Formel für die Entropie. Mit diesem Wert lässt sich errechnen, dass der Informationsgehalt der Zeichenkette 8,49 Bits entspricht.

Nun zum Ablauf. Die folgende Tabelle zeigt die genauen Werte für die Subintervalle nach dem Codieren der einzelnen Zeichen. Die Grafik rechts veranschaulicht die Auswahl der Subintervalle noch einmal.

	Intervall		Intervallgröße
	0 -	1	1
A	0 -	0,75	0,75
A	0 -	0,5625	0,5625
A	0 -	0,421875	0,421875
B	0,31640625 -	0,369140625	0,052734375
A	0,31640625 -	0,35595703125	0,03955078125
A	0,31640625 -	0,3460693359375	0,0296630859375
A	0,31640625 -	0,338653564453125	0,022247314453125
C	0,335872650146484375 -	0,338653564453125	0,002780914306640625

Gespeichert wird eine beliebige, möglichst kurze Zahl aus dem letzten Intervall, also z. B. 0,336.

Das entspricht zwischen 8 und 9 Bits. Die Huffman-Kodierung hätte für die gegebene Zeichenfolge dagegen 10 Bit benötigt (1 für jedes A und je 2 für B und C)

Der Unterschied beträgt in diesem Beispiel 10%. Der Gewinn wird größer, wenn die tatsächlich von der Huffman-Kodierung verwendete Bitzahl mehr von der optimalen abweicht, also wenn ein Zeichen extrem häufig vorkommt.

Der Dekodierer nimmt diese Zahl zum Dekodieren. Dabei läuft Folgendes ab:

• Gestartet wird mit dem Startintervall [0; 1]. Dieses Intervall wird vom Dekodierer in die 3 Teilintervalle zerlegt (so wie in der 1. Zeile vom Bild).
• 0,336 liegt im Subintervall A [0; 0,75]. Also ist das erste Zeichen A.
• Das aktuelle Subintervall wird [0; 0,75]
• [0; 0,75] wird wieder nach dem bekannten Schema zerlegt
• 0,336 liegt wieder im ersten Intervall [0; 0,5625], also A ausgeben.
• ...

Optimalität

Warum ist der arithmetische Kodierer optimal?

Die Größe des Intervalls ist direkt verbunden mit der Anzahl der Nachkommastellen (bzw. Bits), die notwendig sind, um eine Zahl aus diesem Intervall darzustellen (dem so genannten Informationsgehalt). Je kleiner das Intervall, umso mehr Bits sind notwendig. Es gibt Ausnahmen, die es erlauben manchmal weniger Bits zu verwenden, diese Ausnahmen treten aber selten auf.

Ein Beispiel mit dezimalen Zahlen. In einem Intervall der Größe 10 ^{− 3} lässt sich immer eine Zahl mit 3 Stellen nach dem Komma finden. Zwischen 0,11123 und 0,11223 liegt beispielsweise 0,112. Ist die Größe des Intervalls I, so ist die Anzahl der notwendigen Dezimalstellen − log₁₀I.

Um für binäre Zahlen die Anzahl der Bits zu berechnen, wird anstatt mit Zehnerpotenzen und dekadischem Logarithmus (die im Dezimalsystem verwendet werden, siehe oben) mit Zweierpotenzen und dem dyadischen Logarithmus log₂ gerechnet.

Die Anzahl der notwendigen Bits ist also − log₂I.

Nach jedem Kodierungsschritt wird das Intervall um einen Faktor kleiner, der der Wahrscheinlichkeit des Zeichens entspricht, da die Größe der Subintervalle diesen Wahrscheinlichkeiten entspricht. Die neue Intervallgröße ist also 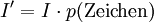$I' = I \cdot p({\rm Zeichen})$. Die Anzahl der für I' benötigten Bits ist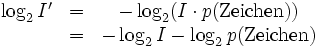

$\begin{matrix}\log_2 I' &=& -\log_2 (I \cdot p({\rm Zeichen})) \\ \ &=&-\log_2 I - \log_2 p({\rm Zeichen}) \end{matrix}$

Es kommen also genau so viele Bits zum Ausgabestrom hinzu, wie die Entropie verlangt. Somit ist die arithmetische Kodierung in Bezug auf den Informationsgehalt optimal.

Implementierung

Da man bei einer konkreten Implementierung nicht mit unendlich genauen reellen Zahlen arbeiten kann, muss die konkrete Umsetzung des Algorithmus etwas anders erfolgen. Die maximale Genauigkeit der Zahlen ist im allgemeinen fest vorgegeben (z. B. 32 Bits) und kann diesen Wert nicht überschreiten. Deshalb kann man einen Arithmetischen Kodierer nicht auf einem realen Computer umsetzen.

Um das Problem der begrenzten Genauigkeit zu umgehen, werden zwei Schritte unternommen:

1. Die Stellen nach der oberen Grenze der Genauigkeit werden abgeschnitten. Das führt dazu, dass die Intervallgrößen nicht mehr exakt mit den geforderten Werten übereinstimmen. Das führt zu einer Verschlechterung des Ergebnisses.
2. Das Intervall muss ab und an wieder vergrößert werden, da sonst nach einigen kodierten Zeichen die Genauigkeit der Zahlen aufgebraucht ist. Deshalb werden höherwertige Stellen, die feststehen, ausgegeben und aus den Zahlen entfernt. Im Beispiel von oben kann man also nach dem Kodieren des Zeichens B sicher sagen, dass die Ergebniszahl mit 0,3 beginnt. Man kann also bereits hier 0,3 ausgeben und von den Intervallgrenzen abziehen. Danach wird die Intervallgrenze mit 10 skaliert, und es wird mit diesem Wert weitergerechnet.

Punkt 1 führt eigentlich dazu, dass der Algorithmus kein Arithmetischer Kodierer mehr ist, sondern nur ähnlich. Es gibt aber einige eigenständige Algorithmen, die vom Arithmetischen Kodierer abstammen; diese sind:

1. Der Range-Coder: dieser Kodierer ist eine relativ direkte Umsetzung des Arithmetischen Kodierers mit Integerzahlen.
2. Der Q-Coder (von IBM entwickelt und patentiert): vereinfacht zusätzlich das Alphabet auf nur zwei Zeichen. Dieses Vorgehen erlaubt eine Annäherung der Intervallaufteilung mit Additionen anstatt Multiplikationen wie beim Range-Coder.
3. Der ELS-Coder: arbeitet auch nur mit zwei Zeichen, ist aber effizienter bei relativ gleich wahrscheinlichen Zeichen, während beim Q-Coder beide Zeichen möglichst unterschiedliche Wahrscheinlichkeiten haben sollten.

Trotz dieser Verfahren bleiben verschiedene Probleme mit der Arithmetischen Kodierung:

• Geschwindigkeit: Arithmetische Kodierer sind relativ aufwendig und langsam. Für jedes Zeichen muss beim Range-Coder eine Division ausgeführt werden. Die anderen Kodierer erfordern das mehrmalige Ausführen des Kodierprozesses für alle Bits des Zeichens.
• Patente: Der Q-Coder ist zwar neben dem Huffman Coder für JPEG erlaubt, wird aber fast nie verwendet, da er von IBM patentiert ist.
• kleiner Gewinn: mit verschiedenen Methoden lässt sich erreichen, dass die viel schnellere Huffman-Kodierung nur unwesentlich schlechtere Ergebnisse liefert als der aufwendige Arithmetische Kodierer. Dazu gehört, dass manchmal Zeichenketten als eigenständige Zeichen behandelt werden. Somit lässt sich der „Verschnitt“ senken, der dadurch entsteht, dass jedes Zeichen mit einer ganzzahligen Bitlänge dargestellt wird.

Weblinks

• Ausarbeitung zu Grundlagen der arithmetischen Kodierung, inkl. Quelltext (E. Bodden et al. 2002)
• Q-Coder Seite von IBM
• Website des Range-Coders, Sourcecode zum Download
• Beschreibung des Algorithmus des Range-Coders in Pseudocode
• Java Applet
• Das elektronische Buch Information Theory, Inference, and Learning Algorithms von David J. C. MacKay erklärt in Kapitel 6 das arithmetische Kodieren.