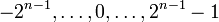B-Komplement

Das Zweierkomplement (auch 2-Komplement, Zweikomplement, B(inär)-Komplement, Basiskomplement, two's complement) ist eine arithmetische Operation auf Dualzahlen. Dabei werden zunächst alle Ziffern bzw. Bits negiert, das heißt aus 0 wird 1 und umgekehrt. Anschließend wird 1 hinzuaddiert. Häufigste Anwendung dürfte die Zweierkomplementdarstellung (auch Zweierkomplementformat, K2-Zahl, 2K-Zahl oder im Jargon auch einfach nur Zweierkomplement) sein, eine Möglichkeit, negative Zahlen im Dualsystem darzustellen. Dabei werden keine zusätzlichen Symbole wie + und − benötigt. Dies ist vor allem für Computer wichtig, deren Logik allein auf Bits, welche entweder wahr oder falsch bzw. 1 oder 0 sind, ausgerichtet ist. Das heißt, binäre Zahlen sind Folgen von 0 und 1. Die Zweierkomplementdarstellung ist die vorherrschende Art, mit der negative ganze Zahlen im Computer dargestellt und für Rechenoperationen mit Hilfe des Rechenwerks erschlossen werden.

Motivation

Da bei binären Kodierungen von negativen Zahlen, welche nicht im Zweierkomplementformat vorliegen, sowohl das Vorzeichen als auch der Betrag durch getrennte Bits dargestellt werden, ist es wichtig, zu wissen, welches Bit wofür verwendet wird. Üblicherweise wird dies erreicht, indem sämtliche Zahlen eine konstante Stellenzahl haben und bei Bedarf mit führenden Nullen aufgefüllt werden, und einem davon getrennten Bit, welches das Vorzeichen codiert. Für die Verarbeitung sind dann entsprechende Steuerlogiken notwendig, welche die unterschiedlichen Bits und deren Bedeutung bewerten.

Bei der Codierung in der Zweierkomplementdarstellung ist hingegen die explizite Unterscheidung zwischen einem ausgezeichneten Vorzeichenbit und jenen Bits, welche den Betrag beschreiben, nicht notwendig. Negative Zahlen sind daran zu erkennen, dass das höchstwertige Bit den Wert 1 hat. Bei 0 liegt eine positive Zahl oder der Wert 0 vor. Der Vorteil dieses Zahlenformates besteht darin, dass für Verarbeitung in digitalen Schaltungen keine zusätzliche Steuerlogiken notwendig sind.

Da in der Zweierkomplementdarstellung der Wert 0 den positiven Zahlen zugerechnet wird, umfasst der Wertebereich bei n binären Stellen allgemein den Bereich:

$-2^{n-1} , \ldots , 0, \ldots , 2^{n-1}-1$

Beispiele:

bei 8 Bit:                  −128(10)  bis                 +127(10)
bei 16 Bit:               −32768(10)  bis               +32767(10)
bei 32 Bit:          −2147483648(10)  bis          [phone](10)
bei 64 Bit: −9223372036854775808(10)  bis +9223372036854775807(10)

Darstellung und Umwandlung aus dem Dezimalsystem

Die Zweierkomplementdarstellung benötigt, anders als die Einerkomplementdarstellung, keine Fallunterscheidung, ob mit negativen oder mit positiven Zahlen gerechnet wird. Das Problem der Einerkomplementdarstellung, zwei Darstellungen für die Null zu haben, tritt nicht auf. Positive Zahlen werden in der Zweierkomplementdarstellung mit einer führenden 0 (Vorzeichenbit) versehen und ansonsten nicht verändert.

Negative Zahlen werden wie folgt aus einer positiven Zahl kodiert: Sämtliche binären Stellen werden negiert und zu dem Ergebnis wird der Wert 1 addiert. (Mathematisch exaktes Verfahren siehe formale Umwandlung.)

Beispielhafte Umwandlung der negativen Dezimalzahl −4 in die Zweierkomplementdarstellung unter Verwendung von 8 binären Stellen:

1. Vorzeichen ignorieren und ins Binärsystem umrechnen: 4₍₁₀₎ = 00000100₍₂₎
2. Invertieren: Not[00000100] = 11111011
3. Eins addieren: 11111011 + 00000001 = 11111100

11111100(2) = −4(10)

Weitere Beispiele:

+127(10) = 01111111(2) = 7F(16)
+  4(10) = 00000100(2) = 04(16) 
+  1(10) = 00000001(2) = 01(16)
   0(10) = 00000000(2) = 00(16)  
−  1(10) = 11111111(2) = FF(16) 
−  4(10) = 11111100(2) = FC(16) 
−127(10) = 10000001(2) = 81(16)
−128(10) = 10000000(2) = 80(16) 

Umwandlung per Hand

Trick zur schnelleren Umwandlung (einer positiven in eine negative Binärzahl) von Hand: Von rechts angefangen, alle Nullen und die erste Eins abschreiben und alle nachfolgenden Stellen invertieren.

1. Fange bei der rechten Stelle (niedrigstwertiges Bit) an.
2. 1. Wenn diese Stelle eine 0 ist, schreibe eine 0 und gehe zu Punkt 3;
   2. Wenn diese Stelle eine 1 ist, schreibe eine 1 und gehe zu Punkt 4.
3. Gehe ein Zeichen nach links und wiederhole Punkt 2.
4. Invertiere alle restlichen Stellen bis zum höchstwertigen Bit.

Alternative

Die Zweierkomplementdarstellung kann man sich auch so veranschaulichen: Alle Bits haben die gleiche Wertigkeit wie bei positiver Darstellung. Das MSB (most significant bit = höchstwertige bit) allerdings erhält die negative Wertigkeit. Durch Subtraktion dieses Bits lassen sich Zahlen sehr schnell umwandeln. Beispiel mit 8-Bit-Binärzahlen in Zweierkomplementdarstellung:

Wertigkeit	−128	64	32	16	8	4	2	1	Dezimal
Bitfolge	0	0	0	1	1	0	1	0	= 26
Bitfolge	1	0	0	1	1	0	1	0	= −102

00011010(2) = 16 + 8 + 2 = 26
10011010(2) = (−128) + 16 + 8 + 2 = −102

Rechenoperationen

Addition und Subtraktion benötigen keine Fallunterscheidung. Die Subtraktion wird auf eine Addition zurückgeführt.

Beispiele an 8 Bit langen Zahlen ohne Vorzeichenerweiterung:

−4 + 3 = −1 führt zu 
  11111100 
+ 00000011 
= 11111111;

 +4 +(− 4) = 0:
           00000100
        +  11111100  
          ---------
        = 100000000

Die vorderste Eins, in diesem Beispiel die 9. Stelle, wird verworfen.

+4 − 3 = +1 führt zu             −4 − 3 = −7 führt zu    
   00000100                         11111100 
+  11111101                      +  11111101
= 100000001                      = 111111001

Auch hier wird das korrekte Ergebnis durch Weglassen der 9. Stelle, in diesen Fällen 1, gebildet.

Solange der gültige n-stellige Zahlenbereich, bei 8 Bit breiten Zahlen der Wertebereich der Summe von −128 bis +127, nicht verlassen wird, funktioniert dieses Vorgehen ohne Vorzeichenerweiterung problemlos. Liegt hingegen der Wertebereich der Summe außerhalb des Intervalls, kommt es zu einem Überlauf, welcher in diesem Zusammenhang häufig und fälschlich mit dem Übertrag verwechselt wird. Die Abhilfe ist eine Vorzeichenerweiterung vor der Rechenoperation.

Vorzeichenerweiterung

Können die beiden Summanden beliebige Werte annehmen, ist für eine korrekte Addition in Zweierkomplementdarstellung eine Vorzeichenerweiterung nötig. Dabei wird von beiden Summanden zunächst die oberste Stelle dupliziert und somit die Stellenanzahl um eins vergrößert. In diesen Beispielen die 8. Stelle, welche auf die 9. Stelle kopiert wird. Anschließend wird die Addition wie oben, aber mit 9 Stellen, durchgeführt. Das Addierwerk muss dazu immer eine Stelle mehr umfassen.

Unterscheiden sich in der berechneten Summe dann die höchstwertige und die Stelle darunter voneinander, ist das Ergebnis nicht mehr im Wertebereich der Summanden darstellbar – es ist ein Überlauf aufgetreten. Je nach Anwendungsfall wird dann mit dem um ein Bit breiteren und korrekten Ergebnis weitergerechnet, oder ein Fehlerabbruch ist die Folge.

Beispiel: Die Addition der beiden positiven Zahlen 50 und 80 ergibt 130 und überschreitet damit den Wertebereich. Die Zahl passt zwar noch in eine 8-Bit-Variable, aber das 8. Bit ist jetzt gesetzt, so dass die Zahl fälschlicherweise negativ erscheint. Manche Mikroprozessoren wie der 6502 melden so ein Ereignis mit einem eigenen Statusbit, hier dem Overflow-Bit O, das der Programmierer nach vorzeichenbehafteten Rechenoperationen abfragt und entsprechend reagieren kann.

Beispiel für Vorzeichenerweiterung, die 9. Stelle der Vorzeichenerweiterung ist zur Verdeutlichung in Klammern geschrieben:

+4 + 127 = +131 führt zu          −4 − 127 = −131 führt zu
   (0)00000100                       (1)11111100
+  (0)01111111                     + (1)10000001
=  (0)10000011                     = (1)01111101

In beiden Fällen unterscheiden sich die 8. und 9. Stelle voneinander, eine Reduktion auf 8 Bit würde zu einem Fehler führen. Zur Verdeutlichung und Vergleich die obigen beiden Beispiele mit Vorzeichenerweiterung:

+4 − 3 = +1 führt zu             −4 − 3 = −7 führt zu    
   (0)00000100                        (1)11111100 
+  (1)11111101                      + (1)11111101
=  (0)00000001                      = (1)11111001

in beiden Fällen unterscheiden sich die 8. und 9. Stelle der Summe nicht, die beiden Ergebnisse können somit korrekt wieder auf 8 Stellen reduziert werden. Generell kann die Stellenanzahl in der Zweierkomplementdarstellung, von oben beginnend, so lange und ohne Verfälschung des Wertes reduziert werden, bis sich die beiden obersten Stellen im Wert voneinander unterscheiden. Dies Verdeutlicht den Umstand, dass bei der Zweierkomplementdarstellung von Zahlen keine fixe Stelle für die Codierung des Vorzeichens existiert.

Multiplikation

Auch die Multiplikation ist in der Zweierkomplementdarstellung im Rahmen von Multiplizierwerken möglich und stellt insbesondere in der digitalen Signalverarbeitung eine Grundfunktion dar. Für die schaltungstechnische Realisierung von Multiplizierwerken gibt es verschiedene Möglichkeiten. Bei einem Parallelmultiplizierer wird das Produkt durch eine Vorzeichenerweiterung, Stellenverschiebung und anschließende Addition gebildet. Die einzelnen Summanden müssen dabei immer auf die Produktlänge vorzeichenerweitert werden.

Bei zwei Faktoren zu je 4 Bit Länge ist das Produkt maximal 8 Bit lang. Oder allgemein: Für n Bit breite Faktoren ist das Produkt 2·n Bit lang und alle Teilsummanden müssen auf diese Länge vorzeichenerweitert werden. An der Operation −7 · −3 in Zweierkomplementdarstellung soll dies verdeutlicht werden:

       1001   (entspricht dezimal der Zahl −7)
     · 1101   (entspricht dezimal der Zahl −3)
     ======
 + 11111001   (1001 · 1, um null Stellen nach links verschoben und mit Vorzeichenerweiterung)
 + 00000000   (1001 · 0, um eine Stelle  nach links verschoben und mit Vorzeichenerweiterung)
 + 11100100   (1001 · 1, um zwei Stellen nach links verschoben und mit Vorzeichenerweiterung)
 − 11001000   (1001 · 1, um drei Stellen nach links verschoben und mit Vorzeichenerweiterung)
 ==========
   00010101   (entspricht dezimal +21)

Die letzte Zeile muss in der Zweierkomplementdarstellung immer subtrahiert werden. Diese Subtraktion kann in schaltungstechnischen Realisierungen entweder durch Volladdierer und deren Umschaltung in den Subtraktionsmodus erfolgen, oder durch Negation der Zeile und der zusätzlichen Addition von +1, analog wie bei der Bildung des Zweierkomplements.

Zur Verdeutlichung eine Multiplikation mit unterschiedlichen Vorzeichen (−7) · 3 in Zweierkomplementdarstellung:

       1001   (entspricht dezimal der Zahl −7)
     · 0011   (entspricht dezimal der Zahl 3)
     ======
 + 11111001   (1001 · 1)
 + 11110010   (1001 · 1)
 + 00000000   (1001 · 0)
 − 00000000   (1011 · 0)
 ==========
   11101011   (entspricht dezimal −21)

Umwandlung ins Dezimalsystem

Wenn man eine Zahl von der Zweierkomplementdarstellung ins Dezimalsystem umkodieren will, muss man folgendermaßen (umgekehrt entsprechend der Umwandlung vom Dezimalsystem in die Zweierkomplementdarstellung) vorgehen:

1. Erste Stelle anschauen: wenn Ziffer = 1: Zahl negativ, Ziffer = 0: Zahl positiv.
2. Zahl ist positiv: Umrechnung vom Binärsystem ins Dezimalsystem ist bereits möglich;
3. Zahl ist negativ: Man subtrahiert 1 und negiert die einzelnen Ziffern. (Dieser Schritt lässt sich für den Menschen vereinfachen: Man negiert zuerst die einzelnen Ziffern und addiert hinterher 1, was zum selben Ergebnis führt.)
4. Die entstandene, entsprechend positive Zahl im Binärsystem rechnet man ins Dezimalsystem um.
5. Wenn negativ, ein "−" vor die Zahl setzen.

Beispiel:

11111101 
1 subtrahieren  = 11111100
invertiert = 00000011
00000011 im Dezimalsystem = 3
3 negativ = −3

11111101 (Zweierkomplementdarstellung) = −3 (Dezimalsystem)

Eine andere Vorgehensweise zur Umwandlung einer Zahl in Zweierkomplementdarstellung in das Dezimalsystem ist die folgende: Habe die Zahl in Zweierkomplementdarstellung n Stellen, gegeben sind also n Bits a_{n − 1}a_{n − 2}a_{n − 3}...a₁a₀:

x_dezimal = − 2^{n − 1} * a_{n − 1} + 2^{n − 2} * a_{n − 2} + 2^{n − 3} * a_{n − 3} + ... + 2¹ * a₁ + 2⁰ * a₀

Formale Umwandlung aus dem Binärsystem

Ist x eine negative Zahl, so errechnet sich x in Zweierkomplementdarstellung (x_z) mit n Stellen wie folgt:

x_z = 2ⁿ − | x |

Dementsprechend gilt auch

x_z + | x | = 2ⁿ

wobei | x | der positiven Zahl entspricht und 2ⁿ bei der Rechnung als Übertrag in der n + 1-sten Stelle auftritt.

Zweierkomplementdarstellung bei Festkommazahlen

Die Zweierkomplementdarstellung kann auch bei Festkommazahlen angewandt werden, womit beispielsweise gebrochene Zahlen wie 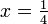$x=\tfrac{1}{4}$ binär dargestellt werden können. Festkommazahlen werden unter anderem im Bereich der digitalen Signalverarbeitung verwendet. Festkommazahlen werden allgemein durch ein Verschieben des Kommapunkts, der sich bei ganzen Zahlen immer rechts hinter der letzten Stelle befindet, gebildet. Dabei wird der Kommapunkt nicht in der Binärdarstellung gespeichert, sondern implizit seine Position als fix angenommen, wovon sich der Name der Festkommadarstellung ableitet.

Somit bleiben die oben genannten Rechenregeln im Prinzip erhalten, lediglich die Werte verändern sich. Zur Bildung einer binären Zweierkomplementärdarstellung müssen sämtliche Binärstellen invertiert und anschließend der Wert einer Quantisierungsstufe 2^k addiert werden. Dabei gibt k die Position der letzten darstellbaren binären Ziffer an. Bei obigen Ganzzahlen wäre dies die Stelle k=0, womit bei der Bildung des Zweikomplementes bei ganzen Zahlen nach der Invertierung der Wert 2⁰=1 addiert werden muss. Ist der Kommapunkt beispielsweise um 2 Stellen nach links verschoben und umfasst das binäre Wort die beiden Stellen rechts vom Kommapunkt, wäre k=−2, und somit muss zur Bildung des Zweierkomplemtes 2⁻²=0,25 addiert werden. (Hinweis: Der Kommapunkt kann bei Festkommazahlen auch außerhalb des darstellbaren Wertebereiches liegen.)

Ein Beispiel soll dies verdeutlichen: Eine binäre Zahl mit fünf Bit Wortlänge besitzt drei Vorkommastellen und zwei Nachkommastellen. Damit kann der Wertebereich −4 bis +3,75 in Schritten von 0,25 dargestellt werden. Die Zahl 2,25 entspricht der binären Zahl 010,01₂. Wird nun das Zweierkomplement davon gebildet, werden alle Stellen der binären Zahl invertiert und 2⁻²=0,25 addiert, was 101,11₂ = −2,25 ergibt.

Verallgemeinerung auf andere Stellenwertsysteme

Auch in anderen Stellenwertsystemen kann man ganze Zahlen ohne Verwendung eines Minuszeichens darstellen. Man hat hier aber das Problem, dass die Unterscheidung von positiven und negativen Zahlen mehr oder weniger willkürlich vereinbart sein kann.

Beschränkt man sich auf n-stellige Zahlen zur Basis b, dann kann man die natürlichen Zahlen von 0 bis bⁿ − 1 darstellen. Legt man eine Zahl in diesem Bereich als die größte positive Zahl fest, dann kann man jede größere Zahl x als Zweierkomplementdarstellung der negativen Zahl x − bⁿ auffassen.

Die Rechenoperation der Negation wird analog durchgeführt wie zur Basis 2: Jede Ziffer z wird durch (b − 1) − z ersetzt, und zur so entstehenden Zahl wird 1 addiert.

Für die Basis b = 5 und die Stellenzahl n = 3 erhält man für −1 diese Darstellung:

• Die Ziffern der 1 sind 001.
• Die Negation der Ziffern ergibt 443.
• Addition von 1 liefert 444.

Damit wird −1 als 444 dargestellt. Die Addition 444 + 001 (zur Basis 5 und Stellenzahl 3) ergibt 000, da der letzte Übertrag wegfällt.

Legen wir in diesem Beispiel die größte positive Zahl als 222 fest (zur Basis 5, dezimal hat diese Zahl den Wert +62), dann ist 223 = −222 die kleinste negative Zahl (dezimal −62). Der Zahlenbereich reicht also von dezimal −62 bis +62.

Zur Basis 10 und Stellenzahl 2 hat man 99 = −01 und 50 = −50, hier hat man also wie zur Basis 2 eine weitere Zahl neben der 0, die mit ihrer Zweierkomplementdarstellung übereinstimmt. Dieses Phänomen tritt mit jeder geraden Basis auf.

Verallgemeinert man diese Schreibweise weiter, indem man unendlich viele Stellen zulässt, erhält man die Möglichkeit, p-adische ganze Zahlen darzustellen.

Literatur

• Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 12 Auflage. Springer, Berlin 2002, ISBN 3-540-42849-6. 

Weblinks

• Ein Applet zum Üben der binären Addition (dort das Register "konegative Zahlen")