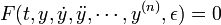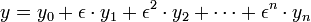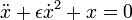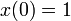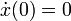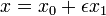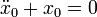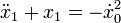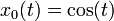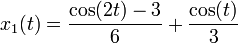Störungsrechnung

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Die Störungsrechnung ist ein Teilgebiet der angewandten Mathematik. Sie wird vor allem in der Physik und Himmelsmechanik eingesetzt und befasst sich mit den Auswirkungen kleiner Störungen auf ein System.

Prinzip der Störungsrechnung

Gegeben sei die Differenzialgleichung n-ter Ordnung

$F(t,y,\dot y,\ddot y,\cdots,y^{(n)},\epsilon)=0$

mit $\epsilon\;$ als kleinen Parameter für den 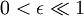$0 < \epsilon \ll 1$ gilt. Zur näherungsweisen Lösung wird die Funktionenreihe

$y=y_0 + \epsilon\cdot y_1 + \epsilon^2\cdot y_2 + \cdots + \epsilon^n\cdot y_n$

benutzt. Einsetzen in die Differenzialgleichung und Koeffizientenvergleich bezüglich $\epsilon\;$ ergibt ein System von Differenzialgleichungen für die Funktionen 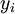$y_i\;$. Die Funktion 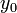$y_0\;$ ist die Lösung des ungestörten Systems mit 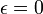$\epsilon = 0\;$. Wenn das ungestörte Problem analytisch lösbar ist kann auch oft mindestens die erste Näherung der Störung analytisch gelöst werden.

Beispiel

Die Differenzialgleichung eines schwingungsfähigen Systems mit Newtonscher Reibung

$\ddot x + \epsilon \dot x^2 +x = 0$

den Anfangsbedingungen

$x(0)=1\;$

$\dot x(0)=0\;$

und dem kleinen Reibungskoeffizienten $\epsilon\;$ ist durch Störungrechnung 1. Ordnung mit dem Ansatz

$x=x_0 + \epsilon x_1\;$

näherungsweise analytisch lösbar. Einsetzen in die Differenzialgleichung und sortieren nach Potenzen von $\epsilon\;$ liefert

das Differenzialgleichungssystem

$\ddot x_0 +x_0=0$

$\ddot x_1 +x_1 = - \dot x_0^2$

und den Anfangsbedingungen

$x_0(0)=1\;$

$\dot x_0(0)=0\;$

$x_1(0)=0\;$

$\dot x_1(0)=0\;$.

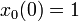
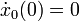
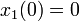
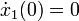Die Lösungen unter Berücksichtigung der Anfangsbedingungen sind

$x_0(t)=\cos(t)\;$

$x_1(t)=\frac{\cos(2t)-3}{6}+ \frac{\cos(t)}{3}$

und damit die Lösung in 1. Störungsordnung

$x=x_0 + \epsilon x_1=\cos(t)+\epsilon \left(\frac{\cos(2t)-3}{6}+ \frac{\cos(t)}{3} \right)$.

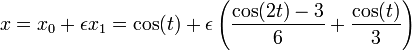Störungsrechnung in der Himmelsmechanik

Bahnstörungen in der Himmelsmechanik sind jene Änderungen der Kepler'schen Ellipsenbahn eines Himmelskörpers um einen anderen, die

1. durch die Gravitation weiterer Körper,
2. durch kleine Bremseffekte von nichtgravitativer Art, oder
3. durch Abweichungen von der Kugelgestalt verursacht werden.

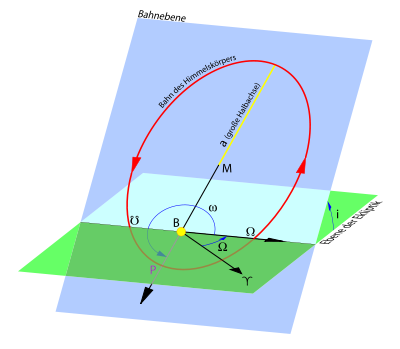
Bahnelemente

Unter der Annahme, dass nur die beiden Hauptkörper existieren und kugel-symmetrisch aufgebaut sind, bewegen sie sich in einem luftleeren Raum nach den drei Keplerschen Gesetzen umeinander. Ihre Bahnen lassen sich durch 6 Bahnelemente vollständig beschreiben und beziehen sich auf den Massenschwerpunkt (Baryzentrum) des Systems. In diesem seit etwa 300 Jahren mathematisch streng gelösten Zweikörperproblem sind die Bahnelemente unveränderlich, wenn das zugrundeliegende Koordinaten-Bezugssystem einem Inertialraum entspricht.

Bahnelemente eines Planeten

Sind aber die drei o.a. Bedingungen nicht vollständig erfüllt - was im Planetensystem deutlich zu merken ist und theoretisch auch im interstellaren Raum -, ändern sich die Bahnelemente (a, e, i, Ω, ω, T) im Laufe der Zeit (t) und die Bewegungen folgen nicht mehr exakt dem Kepler'schen Flächensatz.

Kräftemodelle

Im Regelfall kann angenommen werden, dass die störenden Kräfte klein sind. Dann kann man ihren Einfluss auf die Flugbahnen durch Differentialgleichungen hinreichend genau modellieren und die Änderungen der Bahnelemente (da/dt, de/dt usw.) sind lineare Funktionen der Kräfte.
Bei stärkeren Bahnstörungen sind auch quadratische oder sonstige kompliziertere Modelle erforderlich. Es gibt ferner die Möglichkeit, die (beobachteten) Bahnänderungen durch Reihen, Fourieranalyse etc. zu beschreiben, ohne ihren Ursachen nachzugehen (entsprechend dem Unterschied zwischen Kinematik und Dynamik).

Die Störungsrechnung geht fast ausschließlich¹ im Sinne der Dynamik vor und kennt dabei zwei prinzipielle Vorgangsweisen:

• die Methode der speziellen Störungen mittels "oskulierender" Bahnellipsen, und
• die allgemeine Störungsrechnung mittels der Gravitationstheorie.
• Die nicht-gravitativen Einflüsse und jene durch abgeplattete Himmelskörper treten als weiterer Problemkreis hinzu.

Siehe auch

• Bahnbestimmung, Jarkowski-Effekt, Carl Friedrich Gauß, Laplace, numerische Integration, Periheldrehung
• Störungstheorie (in der Quantenmechanik)