Nutation (Physik)

Rotation (grün), Präzession (blau) und Nutation (rot) eines Kreisels

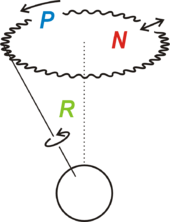
Die Nutation beschreibt in der Physik die Bewegung der Rotationsachse eines Kreisels um die Achse des Drehimpulses. Diese Bewegung wird dadurch verursacht, dass der Drehimpuls L nicht parallel zu einer Figurenachse, d.h. der Achse größten oder kleinsten Trägheitsmoments Θ des Kreisels, ausgerichtet ist. Eine stabile Rotationsachse ist nur bei einer momentenfreien Drehung um eine Figurenachse möglich.

Bei einem momentenfreien Kreisel bewegt sich die Figurenachse auf einem Kreiskegel (=Nutationskegel) mit dem Öffnungswinkel α. Er lässt sich über die Drehimpulskomponenten berechnen.

$\tan (\alpha/2) = { \omega_{\perp} \over \omega_{\|} } {\Theta_{\perp} \over \Theta_{\|} }$

wobei die Indizes für senkrecht bzw. parallel zur Figurenachse stehen.

Herleitung des Nutationskegels: Der Kreisel dreht sich, von außen betrachtet, mit einer Winkelgeschwindigkeit, die zu jedem Zeitpunkt in eine Komponente parallel zur Figurenachse und eine Komponente senkrecht dazu zerlegt werden kann. Auf solche Richtungen beziehen sich die Trägheitsmomente des Kreisels. Für Winkelgeschwindigkeit und Drehimpuls gilt damit

$\vec\omega = \vec{\omega}_\parallel + \vec{\omega}_\perp \qquad \qquad \vec{L} = \Theta_\parallel\vec{\omega}_\parallel + \Theta_\perp\vec{\omega}_\perp = \mathrm{const}$

Der Einheitsvektor in Richtung der Figurenachse rotiert mit dem Kreisel. Somit gilt, von außen betrachtet,

$\dot{\vec{e}}_\parallel = \vec\omega \times \vec{e}_\parallel = \vec{\omega}_\perp \times \vec{e}_\parallel = \frac{\vec{L}}{\Theta_\perp} \times \vec{e}_\parallel$

Man beachte, dass $\vec{\omega}_\perp$ vektoriell nicht konstant ist, so dass erst die letzte Gleichung eine brauchbare Aussage macht. Sie beschreibt eine Drehung der Figurenachse mit der konstanten Winkelgeschwindigkeit

$\vec{\omega}_\mathrm{Nut} = \frac{\vec{L}}{\Theta_\perp}$

Der Winkel zwischen Figurenachse und Drehimpuls, hier α / 2 genannt, bleibt bei der Drehungbewegung konstant. Man kann ihn zu einem beliebigen Zeitpunkt aus dem Verhältnis der Beträge der Drehimpulskomponenten bestimmen, mit dem behaupteten Ergebnis für tan(α / 2).

Die Winkelgeschwindigkeit der Nutationsbewegung ist im Bezugssystem des Kreisels

$\vec \omega_N = { \sqrt{ \omega_\|^2 \Theta_\|^2 + \omega_\perp^2 \Theta_\perp^2 } \over \Theta_\perp } \vec e_\perp$

Unabhängig davon kann ein Kreisel, auf den Momente wirken, auch noch eine Präzessionsbewegung ausführen.

Eine mathematische Beschreibung der Kreiselbewegung wird durch die eulerschen Gleichungen ermöglicht.

Weblinks

• Kreisel mit Rotation, Präzession und Nutation