Nyquist-Stabilität

Die Nyquist-Ortskurve für $G(s)=\frac{1}{s^2+s+1}$.

Das Stabilitätskriterium von Nyquist (auch Strecker-Nyquist-Kriterium, nach Harry Nyquist und Felix Strecker) ist ein Begriff aus dem Bereich der Regelungstechnik und der Systemtheorie. Das Nyquist-Kriterium beschreibt die Stabilität eines Systems mit Rückkopplung, z. B. einem Regelkreis. Beispiele für Regelkreise im Alltag sind der Tempomat im Auto oder die Temperaturregelung im Kühlschrank.

Grundlagen

Man bezeichnet das System als BIBO-stabil (bounded input, bounded output), wenn es auf beschränkte Eingangsgrößen auch mit beschränkten Ausgangsgrößen reagiert. Ein instabiles System hingegen kann schon bei geringen Eingangsstörungen "aus dem Ruder laufen". Ein Stab auf der Fingerspitze ist z. B. ein instabiles System, welches durch das Balancieren stabilisiert wird.

Mathematisch beschreibt man die Eigenschaften der Systeme in der Regelungstechnik mit einer Übertragungsfunktion: Ausgang Y gleich Übertragungsfunktion G mal Eingang W, formal $Y=G \cdot W$.

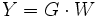Weil die Rechenoperationen dadurch einfacher werden, werden W, G und Y nicht als Funktion der Zeit, sondern als von der (komplexen) Frequenz abhängige Laplacetransformierte angegeben: 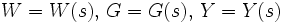$W=W(s),\, G=G(s),\, Y=Y(s)$. s ist ein komplexer Wert, welcher mit der Frequenz über die Formel 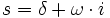$s= \delta + \omega\cdot i$ zusammenhängt.

In einem typischen Regelsystem kann man vier Übertragungsfunktionen ausmachen:

1. Die Übertragungsfunktion der Regelstrecke (Stab auf Finger, Auto mit Gaspedal, Kühlschrank mit Motor) wird G_S(s) genannt.
2. Die Übertragungsfunktion des Reglers (Mensch, Tempomat, Kühlschrankelektronik) wird G_R(s) genannt.
3. Die Multiplikation von 1 und 2 wird Übertragungsfunktion des offenen Regelkreises genannt, $G_R(s)\cdot G_S(s)=G_0(s)$.
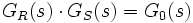4. 1 und 2 bilden zusammen die Übertragungsfunktion des Regelsystems G(s) als Ganzes. Für unsere Beispiele sind dies ein balancierender Mensch, ein Auto mit eingeschaltetem Tempomat oder ein funktionierender Kühlschrank. $G_{geregelt}=\frac{G_{0}}{I-/+G_{0}}$

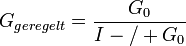
Die Übertragungsfunktionen sind typischerweise Brüche von Polynomen. Solche Polynombrüche haben überall dort, wo das Nennerpolynom eine Nullstelle hat eine Polstelle, der Wert von G strebt dort gegen unendlich.

Das Nyquistkriterium kann, sofern die Übertragungsfunktionen bekannt sind, sagen, ob ein Regelsystem stabil ist oder nicht. Man unterscheidet zwei Fälle. Beide sind nur anwendbar, wenn die Übertragungsfunktion G₀(iω) bei sehr hohen Frequenzen gegen 0 strebt, also der Grad des Nennerpolynomes größer ist als der des Zählerpolynomes.

Spezielles Nyquistkriterium

Haben alle komplexen Polstellen von G_R(s) und G_S(s) einen Realteil kleiner als 0, so besagt das spezielle Nyquistkriterium, dass das gesamte Regelsystem asymptotisch stabil ist, wenn G₀(iω) (also nur ein Teilsystem) für ω von 0 bis $\infty$ in der komplexen Ebene den Punkt 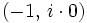$(-1,\, i\cdot 0)$ nicht umläuft. Eine derartige Darstellung wird Ortskurve genannt.

Der Punkt 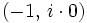$(-1,\, i\cdot 0)$ wird daher auch Nyquist-Punkt oder kritischer Punkt genannt.

Für einfachere Ortskurven kann man alternativ sagen, dass die Kurve den Punkt "-1" links liegen lassen muss damit der geschlossene Kreis stabil ist. Das ist deshalb nötig, da der Punkt -1 auf der reellen Achse der komplexen Ebene einer Phasendrehung um 180° entspricht. Ein Rückkopplungssignal, das als Gegenkopplung wirken soll, besitzt grundsätzlich eine Phasenverschiebung um 180° zum Eingangssignal eines Systems. Tritt nun durch weitere Phasendrehung im Verlauf der stetigen Zunahme der Frequenz eine Phasenverschiebung um weitere 180° auf, dann schwingt das System mit Sicherheit, wenn das rückgekoppelte Signal größer als 1 ist. Es liegt dann links vom Punkt -1 in dieser Ortskurve auf der reellen Achse.

Zum Abgleich des Reglers sind noch zwei Kenngrößen zu beachten. Zum einen die Amplitudenreserve, welche besagt um welchen Faktor die Regelstrecke verstärkt werden darf, um noch stabil zu sein, und zum anderen die Phasenreserve (wichtig bei Systemen mit Totzeit). Die Phasenreserve gibt jenen Winkel an, um den die Phasenlage des rückgekoppelten Signals noch weiter verschoben werden kann bis Mittkopplung (insgesamt 360° Phasendrehung) im System eintritt. Die Phasenreserve ist also der Winkel zwischen der Ursprungsgerade durch den Punkt auf der Ortskurve, der den Abstand 1 zum Ursprung hat (Konstruktion durch Schnittpunkt mit Einheitskreis), und der negativen, reellen Achse.

Allgemeines Nyquistkriterium

Das allgemeine Nyquistkriterium ist auch für Fälle anwendbar, wo die Voraussetzung für das spezielle Nyquistkriterium nicht erfüllt ist. Die Voraussetzungen zur Anwendung sind schwächer, es muss lediglich gelten, dass keine Polstellen der Strecke und des Reglers auf der imaginären Achse 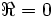$\Re=0$ liegen.

Im Gegensatz zum speziellen Nyquistkriterium muss man hier den Verlauf von G₀(iω) in Abhängigkeit von iω auch für negative Omega aufzeichnen.

Jetzt kann man folgende Bezeichnungen einführen:

• P ist die Anzahl instabiler Polstellen des offenen Regelkreises G₀. Instabile Polstellen sind solche mit positivem Realteil.

• N ist die Anzahl instabiler Polstellen des gesamten Regelsystems G.

• U ist die Anzahl Umläufe der Frequenzgangskurve des offenen Regelkreises G₀(iω) um den Nyquistpunkt. Dabei fährt man in positive ω-Richtung und zählt Umläufe im Gegenuhrzeigersinn positiv, solche im Uhrzeigersinn negativ.

Das allgemeine Nyquistkriterium besagt erstens, dass in jedem Falle N = P − U gilt.

Zweitens ist das Regelsystem asymptotisch stabil, wenn P = U gilt, anderenfalls ist es instabil.

Nyquist-Punkt

Der Begriff Nyquistpunkt wird in der Literatur gelegentlich auch für die Nyquist-Frequenz verwendet, was einige Verwirrung stiftet.

Nyquistkriterium für Mehrgrößensysteme

Das Nyquistkriterium lässt sich auch für Mehrgrößensysteme verwenden. Die Ortskurve der offenen Strecke muss durch die Kurve der Determinante von 1 + G₀ ersetzt werden und der kritische Punkt -1 durch den Punkt 0.

Andere Kriterien

Das Hurwitzkriterium ist eine Alternative zum Nyquistkriterium.

Siehe auch

• Ringoszillator
• Oszillatorschaltung#Schwingungsbedingung
• Operationsverstärker#Verstärkungs-Bandbreiteprodukt

Literatur

• Geering: Regelungstechnik, Springer 2001, ISBN 3-540-41264-6