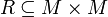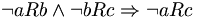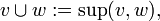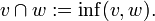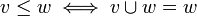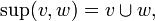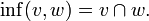- Oberhalb-Menge
-
In der Mathematik sind Ordnungsrelationen Verallgemeinerungen der „kleiner-gleich“-Beziehung. Sie erlauben es, Elemente einer Menge miteinander zu vergleichen.
Eine Ordnungsrelation ist formal eine zweistellige Relation
auf einer Menge M mit bestimmten, unten bei „Halbordnung“ genannten Eigenschaften.
Ist eine Menge M mit einer Ordnungsrelation R gegeben, dann nennt man das Paar (M,R) eine geordnete Menge. Meist bevorzugt man an Stelle der Schreibweise
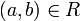 die sogenannte Infix-Notation
die sogenannte Infix-Notation 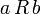 . Außerdem wird für Ordnungsrelationen in den seltensten Fällen ein Symbol wie R verwendet. Stattdessen verwendet man häufig das Symbol „
. Außerdem wird für Ordnungsrelationen in den seltensten Fällen ein Symbol wie R verwendet. Stattdessen verwendet man häufig das Symbol „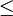 “ oder ähnliche Symbole. Die Schreibweise a < b verwendet man als Abkürzung für „
“ oder ähnliche Symbole. Die Schreibweise a < b verwendet man als Abkürzung für „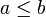 und
und 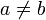 “. Dies erweist sich als zweckmäßig, da für Relationen größtenteils Rechenregeln gelten, die denen in
“. Dies erweist sich als zweckmäßig, da für Relationen größtenteils Rechenregeln gelten, die denen in  (mit gewohntem „
(mit gewohntem „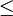 “) entsprechen.
“) entsprechen.Eine (totale) Ordnung auf einer abzählbaren Menge liefert eine Anordnung der Elemente in einer bestimmten Reihenfolge, zum Beispiel die Anordnung der Buchstaben A bis Z im lateinischen Alphabet. Die Reihenfolge der Buchstaben ist willkürlich festgelegt, und jede andere Reihenfolge wäre ebenfalls eine Ordnung.
Es folgt eine Auflistung verschiedener Arten von Ordnungsrelationen mit Beispielen. Für Definitionen der Eigenschaften siehe transitiv, reflexiv und irreflexiv, asymmetrisch, antisymmetrisch oder den Artikel Relation (Mathematik).
Inhaltsverzeichnis
Quasiordnung
Eine Quasiordnung ist transitiv und reflexiv.
Beispiel:
Für komplexe Zahlen
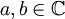 ist die über den Absolutbetrag durch
ist die über den Absolutbetrag durch 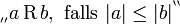 festgelegte Relation eine Quasiordnung: Es gilt die
festgelegte Relation eine Quasiordnung: Es gilt die- Transitivität, denn aus
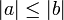 und
und 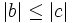 folgt
folgt 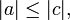 und die
und die - Reflexivität, denn
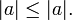
Diese Quasiordnung ist nicht antisymmetrisch, denn betragsgleiche Zahlen müssen nicht identisch sein.
Halbordnung
Eine Halbordnung – auch Partialordnung, teilweise Ordnung, Teilordnung oder partielle Ordnung genannt - ist eine antisymmetrische Quasiordnung (vgl. o.). Halbordnungen können in sogenannten Hasse-Diagrammen visualisiert werden. Eine Teilmenge einer halbgeordneten Menge heißt Oberhalbmenge, wenn sie zu jedem ihrer Elemente auch alle nachfolgenden Elemente (also alle, die rechts vom Relationssymbol stehen könnten) enthält.
Beispiele:
Jede Teilmengenbeziehung
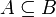 auf einem System
auf einem System 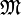 von Mengen ist eine Halbordnung, denn sie ist
von Mengen ist eine Halbordnung, denn sie ist- transitiv, da die Teilmenge einer Teilmenge von A auch Teilmenge von A ist:
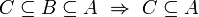 für alle
für alle 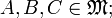
- reflexiv, da jede Menge eine Teilmenge ihrer selbst ist:
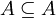 für alle
für alle 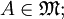
- und antisymmetrisch, da nur A selbst sowohl Teilmenge als auch Obermenge von A ist:
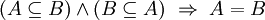 für alle
für alle 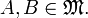
Weitere Beispiele sind die Relation komponentenweise-kleiner-oder-gleich in einem Raum von n-Tupeln und die Teilerbeziehung unter den natürlichen oder ganzen Zahlen, die wie folgt definiert sind:
- komponentenweise-kleiner-oder-gleich,
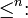 Für zwei Tupel (und eine fest gewählte Zahl n) aus einer Menge V von n-Tupeln gilt:
Für zwei Tupel (und eine fest gewählte Zahl n) aus einer Menge V von n-Tupeln gilt:
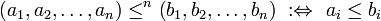 für jedes
für jedes 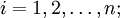
- Teilerbeziehung,
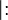 Für zwei natürliche oder ganze Zahlen gilt:
Für zwei natürliche oder ganze Zahlen gilt:
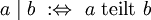 .
.
Weitere Anwendung der Halbordnung
Um den Grad der Vorsortiertheit einer Menge zu messen, kann man die Anzahl der möglichen Fortsetzungen einer Halbordnung zu einer linearen Ordnung angeben. Ist beispielsweise die geordnete Menge
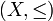 mit X = {a,b,c} und
mit X = {a,b,c} und 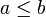 gegeben, so gibt es drei mögliche Fortsetzungen:
gegeben, so gibt es drei mögliche Fortsetzungen: 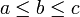 ,
, 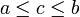 und
und 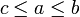 . Der Grad der Vorsortiertheit ist also in diesem Fall
. Der Grad der Vorsortiertheit ist also in diesem Fall 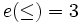 . Nach dem efficient comparison theorem werden für eine vollständige Sortierung der vorsortierten Menge dann nur noch
. Nach dem efficient comparison theorem werden für eine vollständige Sortierung der vorsortierten Menge dann nur noch 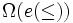 Vergleiche benötigt. In der Informatik nutzt zum Beispiel das Sortierverfahren Mergesort diese Eigenschaft.
Vergleiche benötigt. In der Informatik nutzt zum Beispiel das Sortierverfahren Mergesort diese Eigenschaft.Minimale, maximale und andere Elemente
Sei T eine Teilmenge einer partiell geordneten Menge P.
Wenn m in T die Eigenschaft hat, dass es kein x in T mit x<m gibt, dann heißt m minimales Element von T. Falls es ein Element m in T gibt, das ≤ allen anderen Elementen von T ist, dann heißt m das kleinste Element von T. Ein kleinstes Element von T (wenn es das gibt; z. B. hat die Menge der ganzen Zahlen kein kleinstes Element) ist immer eindeutig bestimmt, und natürlich auch minimal. In einer Totalordnung bedeutet „kleinstes Element“ und „minimales Element“ dasselbe, aber in allgemeinen Halbordnungen kann eine Menge mehrere minimale Elemente haben, von denen dann keines das kleinste ist. Es kann sogar vorkommen, dass eine (unendliche) Menge T zwar ein einziges minimales Element hat, dieses aber nicht das kleinste Element der Menge ist.
Wenn T eine Teilmenge von P ist, und p in P die Eigenschaft hat, dass für alle t in T die Beziehung p≤t gilt, dann heißt p eine untere Schranke von T. (p kann, muss aber nicht Element von T sein.) Wenn es eine größte untere Schranke der Menge T gibt, dann nennt man diese auch die untere Grenze oder das Infimum von T. Jede untere Schranke ist also kleiner als oder gleich dem Infimum.
Analog sind die Begriffe maximales Element, größtes Element, obere Schranke und obere Grenze bzw. Supremum definiert.
Eine Menge, die sowohl eine obere wie eine untere Schranke hat, heißt beschränkt. (Analog sind „nach oben beschränkt“ und „nach unten beschränkt“ definiert.)
Man nennt eine Funktion f, die eine beliebige Menge X in eine partiell oder total geordnete Menge (siehe unten) P abbildet, beschränkt, wenn die Menge der Funktionswerte beschränkt ist, also wenn es ein p und ein q in P gibt, so dass für alle x in X gilt:
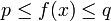 .
.Striktordnung
Eine strenge Ordnung oder Striktordnung ist transitiv und asymmetrisch. Sie unterscheidet sich von der Halbordnung dadurch, dass kein Element zu sich selbst in Beziehung steht. Eine Relation ist transitiv und asymmetrisch genau dann, wenn sie transitiv, irreflexiv und antisymmetrisch ist. Die Kombination von Irreflexivität und Antisymmetrie wird gerade durch den Begriff Asymmetrie zusammengefasst. Eine Striktordnung ist also auch asymmetrisch.
Beispiel: Die Relation „Echte Teilmenge“ in einer Potenzmenge oder die Relation „komponentenweise kleiner, aber nicht gleich“ auf dem Vektorraum
 .
.Strenge schwache Ordnung
Eine strenge schwache Ordnung R ist eine Striktordnung, bei der zusätzlich negative Transitivität gilt:
Totalordnung
Eine Totalordnung, Anordnung oder lineare Ordnung ist eine Halbordnung, die zudem eine totale Relation ist, das heißt für je zwei beliebige Elemente a,b der Grundmenge mit a ≠ b ist stets mindestens eine der beiden Relationen
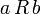 oder
oder 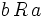 erfüllt. Der Begriff linear orientiert sich an der Vorstellung, die ganze Menge in einer Sequenz
erfüllt. Der Begriff linear orientiert sich an der Vorstellung, die ganze Menge in einer Sequenz 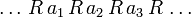 aufzuzählen. Daher leitet sich auch die Bezeichnung Kette für eine totalgeordnete Menge ab.
aufzuzählen. Daher leitet sich auch die Bezeichnung Kette für eine totalgeordnete Menge ab.Ein Beispiel ist die Relation
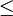 („kleinergleich“) auf den ganzen Zahlen
(„kleinergleich“) auf den ganzen Zahlen 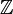 . Ein Gegenbeispiel ist die Teilmengenbeziehung auf der Potenzmenge von
. Ein Gegenbeispiel ist die Teilmengenbeziehung auf der Potenzmenge von 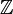 : sie ist nicht total, weil für
: sie ist nicht total, weil für 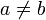 weder
weder 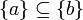 noch
noch 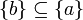 gilt.
gilt.Strenge Totalordnung
Eine strenge Totalordnung (M, < ) ist transitiv und trichotomisch:
Trichotomisch bedeutet: Zwischen zwei Elementen a, b besteht immer genau eine der Beziehungen
- a < b, a = b oder b < a.
„Totalordnung“ bedeutet hier, dass sich zwei beliebige Elemente stets vergleichen lassen. „Total“ im oben erklärten Sinn ist also die zu „<“ gehörige Halbordnung „<“ oder „=“.
Mit Hilfe des Auswahlaxioms kann man beweisen, dass jede Halbordnung in eine Totalordnung eingebettet werden kann. Für endliche Mengen muss man das Auswahlaxiom nicht voraussetzen, und in diesem Fall gibt es zur Konstruktion einer solchen Totalordnung auch explizite Algorithmen, siehe Topologische Sortierung.
Induktive Ordnung
Eine partiell geordnete Menge
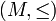 heißt induktiv geordnet, wenn jede linear geordnete Teilmenge von A eine obere Schranke besitzt. Sie heißt streng induktiv geordnet, wenn jede linear geordnete Teilmenge eine kleinste obere Schranke besitzt.
heißt induktiv geordnet, wenn jede linear geordnete Teilmenge von A eine obere Schranke besitzt. Sie heißt streng induktiv geordnet, wenn jede linear geordnete Teilmenge eine kleinste obere Schranke besitzt.Nach dem Lemma von Zorn besitzt jede induktiv geordnete Menge ein maximales Element.
Fundierte Ordnung
Eine fundierte Ordnung ist eine Halbordnung, in der es keine unendlichen, echt absteigenden Ketten gibt (oder, äquivalent formuliert: bei der jede nichtleere Teilmenge ein minimales Element besitzt). Beispiel: Die Teilbarkeitsbeziehung | zwischen natürlichen Zahlen.
Wohlquasiordnung
Eine Wohlquasiordnung ist eine Quasiordnung mit der Eigenschaft, dass es zu jeder Folge
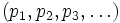 zwei natürliche Zahlen k < n gibt, so dass
zwei natürliche Zahlen k < n gibt, so dass 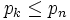 gilt.
gilt.Wohlordnung
Eine Wohlordnung ist eine totale Ordnung, bei der jede nichtleere Teilmenge ein kleinstes Element besitzt.
- Beispiel: „Kleinergleich“ auf den natürlichen Zahlen
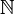 .
. - Beispiel: Die ganzen Zahlen
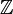 mit der Ordnung 0 < 1 < -1 < 2 < -2 < 3 < -3 <. ...
mit der Ordnung 0 < 1 < -1 < 2 < -2 < 3 < -3 <. ... - Beispiel: Die ganzen Zahlen
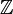 mit der Ordnung 0 < 1 < 2 < 3 <. .. < -1 < -2 < -3 <. ...
mit der Ordnung 0 < 1 < 2 < 3 <. .. < -1 < -2 < -3 <. ...
Das so genannte Wohlordnungsprinzip garantiert die Existenz einer Wohlordnung für jede Menge, zum Beispiel auch für die reellen Zahlen
 . Das Wohlordnungsprinzip folgt aus dem Auswahlaxiom, ist ohne dieses aber nicht beweisbar.
. Das Wohlordnungsprinzip folgt aus dem Auswahlaxiom, ist ohne dieses aber nicht beweisbar.Baum
Ein Baum ist eine partielle Ordnung (T, < ), so dass für jedes
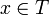 die Menge {y | y < x} der Vorgänger von x wohlgeordnet ist.
die Menge {y | y < x} der Vorgänger von x wohlgeordnet ist.Verbandsordnung
Eine Verbandsordnung ist eine Halbordnung, in der es zu je zwei Elementen v und w immer ein Supremum
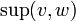 und ein Infimum
und ein Infimum 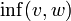 gibt.
gibt.Durch jede Verbandsordnung ist die algebraische Struktur eines Verbandes gegeben, in dem man für je zwei Elemente v und w definiert:
Umgekehrt lässt sich in jedem Verband durch
für je zwei Elemente v und w eine Verbandsordnung definieren, so dass
Eine verbandsgeordnete Menge wird daher oft Verband genannt, sie selbst ist jedoch im Gegensatz zum Verband keine algebraische Struktur.
Vollständige Halbordnung
Eine vollständige Halbordnung (engl. complete partial order, CPO) ist eine partielle Ordnung mit der Eigenschaft, dass jede Teilmenge, die eine aufsteigende Kette
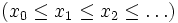 bildet, ein Supremum besitzt. Das Supremum muss dabei nicht in der Teilmenge selbst liegen. Eine vollständig geordnete Menge besitzt immer ein Minimum, denn das Minimum ist Supremum der leeren Menge.
bildet, ein Supremum besitzt. Das Supremum muss dabei nicht in der Teilmenge selbst liegen. Eine vollständig geordnete Menge besitzt immer ein Minimum, denn das Minimum ist Supremum der leeren Menge.Bei einer gerichteten vollständigen Halbordnung (engl. directed complete partial order, DCPO) muss im Gegensatz zur vollständigen Halbordnung die leere Menge kein Supremum besitzen. Es muss damit kein kleinstes Element geben.
Verwendung der Begriffe
Verschiedene Autoren benutzen den Begriff „Ordnung“ unterschiedlich. Er kann eine Halbordnung oder eine totale Ordnung bezeichnen. Man findet also oft entweder die Bezeichnungen
- Ordnung (= Halbordnung) und totale Ordnung
oder die Bezeichnungen
- Halbordnung und Ordnung (= totale Ordnung).
Wikimedia Foundation.