Ordinales Merkmal

Die Ordinalskala ist eines der fünf wichtigsten Skalenniveaus in der Statistik. Bei der Verwendung von ordinal(skaliert)en Merkmalen werden die Merkmalsausprägungen der Untersuchungseinheit genau einer Kategorie zugeordnet und können mit Namen (z. B. „gut“,„mittel“, „schlecht“) oder Zahlen (z. B. „1.“,„2.“,„3.“) bezeichnet werden. Zusätzlich lassen sich die Kategorien in eine Rangfolge bringen. Allerdings müssen die Abstände zwischen den einzelnen Kategorien nicht unbedingt gleich sein (z. B. Rangplätze beim Zieleinlauf in einem Wettkampf sagt nichts über die tatsächliche zeitliche Differenz zwischen dem Zieleinlauf der Wettkämpfer(-innen)). Dazu müssten die Daten mindestens das Skalenniveau „intervallskaliert“ aufweisen.

Werden die Kategorien mit Zahlen bezeichnet, sollen diese so gewählt werden, dass die Rangfolge der Zahlen gleich der Rangfolge der Stärke der Merkmalsausprägungen ist. D.h. jemand mit einem höheren Rang hat auch eine höhere Merkmalsausprägung als jemand mit einem niedrigeren Rang. Über die Stärke der Merkmalsausprägung oder die Größe des Merkmalsunterschiedes zwischen Objekten lässt sich aber keine Aussage machen.

Formale Bedingungen (zusätzlich zu den Bedingungen der Nominalskala):

• Konnexivität

Es gilt entweder a größer b, oder b größer a, oder a gleich b.

• Transitivität

Wenn a größer b und b größer c, dann muss a größer c gelten.

Beispiele

Nachfolgende Tabelle enthält Beispiele für ordinalskalierte Merkmale.

Merkmal	Kategorien
Energieeffizienzklassen	„A“ besser als „B“ besser als „C“ besser als „D“ besser als „E“ besser als „F“ besser als „G“
Einkommen1	hoch > mittel > niedrig
Schulnoten	sehr gut > gut > befriedigend > ausreichend > mangelhaft > ungenügend
Zufriedenheit mit einem Produkt	sehr zufrieden > eher zufrieden > eher unzufrieden > sehr unzufrieden
Dienstgrad beim Militär	General > Oberst > Gefreiter

¹ Wird das Einkommen in Klassen eingeteilt (z. B. 0 bis 999 Euro, 1000 bis 2000 Euro, über 2000 Euro), handelt es sich um ein ordinal skaliertes Merkmal. Wird dagegen der genaue Betrag erhoben und statistisch verarbeitet, liegt ein metrisches Merkmal vor. Da die Auskunftsbereitschaft bei der Angabe des genauen Einkommens geringer ist, wird in vielen Umfragen auf eine Abfrage der Einkommensklassen zurückgegriffen.

Mögliche Operationen

Auch wenn Kategorien durch Zahlen kodiert werden, sind mathematische Operationen mit diesen Zahlen nicht sinnvoll, da sie keinen numerischen Wert, sondern eine Kategorie (z. B. zufrieden) darstellen. So ist beispielsweise eine Division „zufrieden/unzufrieden“ wenig sinnvoll. Da es sich bei Schulnoten in der Regel um ordinalskalierte Merkmale handelt, ist die Bildung von Durchschnittsnoten eigentlich nicht sinnvoll, wird aber in Bildungseinrichtungen regelmäßig durchgeführt. Qualitative Vergleiche („größer/kleiner als“) können allerdings durchgeführt werden.

Ebenfalls möglich ist das Bestimmen von Auftrittshäufigkeiten der Kategorien in einer Menge von Untersuchungsobjekten (oder das Bestimmen von Auftrittshäufigkeiten von Merkmalsausprägungen kleiner oder größer als eine bestimmte Kategorie).

Erlaubte Transformationen

Sämtliche Transformationen mittels (streng) monoton steigender Funktionen sind zulässig.

Mathematische Deutung

Aus mathematischer Sicht ist eine Ordinalskala S eine Menge, für die folgendes gilt:

1. Es existiert eine Äquivalenzrelation 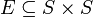$E \subseteq S \times S$, nämlich die Identitätsrelation auf S: $E = id_S = \left\{ \left(m,m\right) \vert m \in S \right\}$.
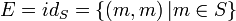2. Es existiert eine lineare Ordnungsrelation $O \subseteq S \times S$.

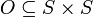Jedes Element 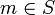$m \in S$ heißt Ausprägung von S.

Jede Ordinalskala ist, als Untermenge, eine Nominalskala.

Die Beschränkung auf das ordinale Messniveau und seine Konsequenzen

Utilitaristen nehmen an, dass Unterschiede im Wohlergehen der Individuen messbare Größen sind. Demnach sind also Aussagen möglich wie z. B.: „Bei Realisierung der Alternative x erhöht sich das Wohlfahrtsniveau des Individuums A um 10 Nutzeneinheiten.“

Mit dem Vordringen des Positivismus und Behaviorismus in Ökonomie und Psychologie geriet das Konzept eines „felicific calculus“ (Bentham) zunehmend in die Kritik. Man wollte eine werturteilsfreie Wissenschaft, die sich allein auf beobachtbare Fakten stützte. So sind innerpsychischen Phänomene nicht direkt (objektiv) beobachtbar. Sie sind nur dem jeweiligen Individuum introspektiv zugänglich.

Beobachtbar ist jedoch das Entscheidungsverhalten der Individuen. Anhand der Wahlhandlungen eines Individuums kann man dessen Präferenzstruktur bestimmen und Aussagen machen wie: „Individuum A hat die Alternative x der Alternative y vorgezogen. X ist für das betreffende Individuum also besser als y“ oder „Für Individuum B sind die Alternativen x und y gleichwertig, denn es hat weder x gegenüber y noch umgekehrt y gegenüber x vorgezogen.“

Hinzu kam, dass die Indifferenzkurven und Präferenzordnungen ausreichten, um die Marktvorgänge zumindest auf der Ebene des theoretischen Modells erklären zu können. Nutzeneinheiten wurden nicht mehr benötigt.

Schwieriger war diese Entwicklung für die normative ökonomische Theorie, die Wohlfahrtsökonomie (engl. 'welfare economics'), auf die man nicht völlig verzichten wollte. Der behavioristische Ansatz wandte sich nicht nur gegen die quantitative Messung des Nutzens, sondern er bot auch keine Grundlage für eine interpersonell vergleichbare Messung des Nutzens. Die Vorteile des einen Individuums können nicht gegen die Nachteile eines andern Individuums aufgerechnet werden.

Damit schrumpfte das utilitaristische Konzept des maximalen gesellschaftlichen Nutzens auf das Konzept der Pareto-Optimalität zusammen. Optimal in diesem Sinne sind Situationen, in denen kein Individuum besser gestellt werden kann, ohne zugleich irgendein anderes schlechter zu stellen.

In dieser Situation wirkte das Arrow-Theorem wie ein Paukenschlag. Arrow wies nach, dass eine Ableitung der Wohlfahrt des Ganzen aus der Wohlfahrt der Einzelnen unter bestimmten, ethisch plausiblen Bedingungen nicht möglich ist, sofern Unterschiede im Wohlergehen der Individuen nur ordinal durch eine entsprechende Rangordnung erfasst werden.

Skalenniveaus

Nominalskala | Ordinalskala | Intervallskala | Verhältnisskala | Absolutskala