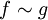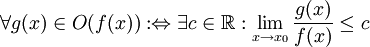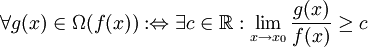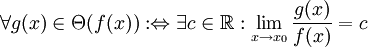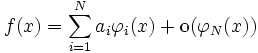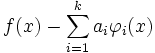Asymptotische Entwicklung

In der Mathematik und ihren Anwendungen, insbesondere in der Komplexitätstheorie, bezeichnet asymptotische Analyse eine Methode um das Grenzverhalten von Funktionen zu klassifizieren, indem man nur den wesentlichen Trend des Grenzverhaltens beschreibt.

Beschreibung des asymptotischen Verhaltens

Das asymptotische Verhalten von Funktionen lässt sich mit einer Äquivalenzrelation beschreiben. Sind beispielsweise f und g reellwertige Funktionen natürlicher Zahlen n, so lässt sich eine Äquivalenzrelation definieren durch

$f \sim g$

genau dann wenn

$\frac{f(n)}{g(n)} \to 1 \mathrm{\ f\ddot{u}r\ } n\to\infty$.

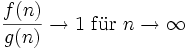Die Äquivalenzklassen von g bestehen aus allen Funktionen h, bei denen der relative Fehler zu g beim Grenzübergang 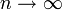$n\to\infty$ gegen 0 strebt. Diese Definition lässt sich unmittelbar auf Funktionen einer reellen oder komplexen Veränderlichen x übertragen sowie auf den Fall x gegen x₀, wobei die Annäherung an x₀ oft nur über eine Teilmenge erfolgt..

Einige Beispiele für asymptotische Resultate

• Der Primzahlsatz der Zahlentheorie besagt, dass die Anzahl von Primzahlen kleiner x für große x sich asymptotisch verhält wie x/log(x).
• Die Stirling-Formel beschreibt das asymptotische Verhalten von den Fakultäten.
• Drei elementare Beispiele sind sin(x), 1 − cos(x) und cot(x) mit dem asymptotischen Verhalten x, x² / 2 bzw. 1/x für x gegen 0.

Landau-Notation

Eine nützliche Notation zur Beschreibung der Wachstumsklassen ist die Landau-Notation, die ursprünglich von Paul Bachmann stammt, aber durch Edmund Landau bekannt gemacht wurde. Eine wichtige Anwendung der Landau-Notation ist die Komplexitätstheorie, in der asymptotische Laufzeit und Speicherverbrauch eines Algorithmus untersucht werden.

Die einfachste Art, diese Symbole zu definieren, ist die folgende: O(f(x)),Ω(f(x)),Θ(f(x)) sind Klassen von Funktionen mit den folgenden Eigenschaften.

$\forall g(x) \in O(f(x)):\Leftrightarrow \exists c \in \mathbb R : \lim\limits_{x\to x_0} \frac{g(x)}{f(x)} \le c$

$\forall g(x) \in \Omega(f(x)):\Leftrightarrow \exists c \in \mathbb R : \lim\limits_{x\to x_0} \frac{g(x)}{f(x)} \ge c$

$\forall g(x) \in \Theta(f(x)):\Leftrightarrow \exists c \in \mathbb R : \lim\limits_{x\to x_0} \frac{g(x)}{f(x)} = c$

x₀ wird in der Regel aus dem Kontext klar. Weiter schreibt man gerne statt 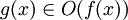$g(x) \in O(f(x))$ das Folgende: g(x) = O(f(x)). Die drei Definitionen sind missverständlich und definieren alle dieselbe Klasse von Funktionen, wenn c in Abhängigkeit von g gewählt wird. Wird dagegen c für die Klassen einheitlich gewählt, so ist zumindest die Definition für das O-Symbol absolut unüblich. Üblich ist, dort das lim-Zeichen wegzulassen und den Quotienten g/f zwischen Betragsstriche zu setzen. Außerdem ist diese Definition durch eine solche für das o-Symbol zu ergänzen, das im nächsten Abschnitt „Asymptotische Entwicklung“ vorkommt.

Asymptotische Entwicklung

Unter einer asymptotischen Entwicklung einer Funktion f(x) versteht man die Darstellung der Funktion als divergente (oder zumindest nicht notwendigerweise konvergente) Reihe. Die Partialsummen einer solchen Reihe brauchen nicht zu konvergieren, liefern aber in der Nähe von x₀ gute Näherungen für den Funktionswert. Das bekannteste Beispiel einer asymptotischen Entwicklung ist die stirlingsche Reihe als asymptotische Entwicklung für die Fakultät. Definieren lässt sich eine solche Entwicklung mit Hilfe einer asymptotischen Folge 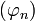$(\varphi_n)$ als

$f(x) = \sum_{i=1}^N a_i\varphi_i(x) + \hbox{o}(\varphi_N(x))$

mit $\varphi_{n+1}(x) = \hbox{o}(\varphi_n(x)), \; x \to x_0$.

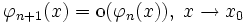Falls die asymptotische Entwicklung nicht konvergiert, gibt es für jedes Funktionsargument x einen Index k, bei dem der Approximationsfehler

$f(x)-\sum_{i=1}^k a_i\varphi_i(x)$

am kleinsten wird; Hinzufügen weiterer Terme verschlechtert die Approximation. Der Index k der besten Approximation wird bei asymptotischen Entwicklungen aber um so größer, je näher x bei x₀ liegt.

Asymptotische Entwicklungen treten insbesondere bei der Approximation gewisser Integrale auf, beispielsweise mittels der Sattelpunktmethode. Das asymptotische Verhalten von Reihen lässt sich darauf oft mit Hilfe der eulerschen Summenformel zurückführen.

Literatur

• Erdélyi, A.: Asymptotic Expansions, New York: Dover, 1987.

• Berg, L.: Asymptotische Darstellungen und Entwicklungen, Berlin: VEB Deutscher Verlag der Wissenschaften, 1968.