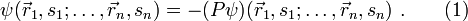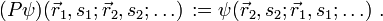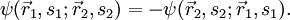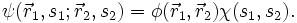Pauliprinzip

Das Pauli-Prinzip (auch paulisches Ausschlussprinzip) ist ein wichtiges, experimentell entdecktes Prinzip der Quantenmechanik und hängt mit dem Spin zusammen. Es ist nach seinem Entdecker Wolfgang Pauli benannt. Es besagt, dass bei Vertauschung von Fermionen die Wellenfunktion antisymmetrisch ist. Daraus ergibt sich insbesondere, dass Elektronen (oder andere Fermionen), die den gleichen Raum belegen, nicht in allen Quantenzahlen übereinstimmen dürfen. Das Pauli-Prinzip bestimmt entscheidend den atomaren Aufbau; eine Folge davon ist u.a., dass normale Materie nicht beliebig kondensierbar ist.

Spezielle Form (Pauli-Verbot)

In seiner zuerst beobachteten und einfachsten Form gilt, dass in einem Atom keine zwei Elektronen in allen vier Quantenzahlen, die zu seiner Zustandsbeschreibung im Atommodell notwendig sind, übereinstimmen dürfen. Dadurch ergibt sich der Aufbau des Periodensystems der Elemente. Die vier relevanten Quantenzahlen im Atom sind dabei die Haupt-, Neben- und die Spinquantenzahl, sowie die Magnetische Quantenzahl, wobei die Hauptquantenzahl im Schalenmodell der Schale entspricht, auf der sich ein Elektron befindet.

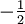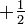Aufgrund des Pauli-Prinzips kann in der Orbital-Theorie ein Orbital nur jeweils zwei Elektronen aufnehmen. Die beiden Elektronen müssen sich in der Spinquantenzahl, welche nur die Werte $-\tfrac 1 2$ und $+\tfrac 1 2$ annehmen kann, unterscheiden.

Allgemeine Form (verallgemeinertes Pauli-Prinzip)

Formulierung

Die Gesamtwellenfunktion 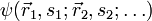$\psi(\vec r_1,s_1;\vec r_2,s_2; \dots )$ eines Systems von n Fermionen muss total antisymmetrisch bezüglich der Vertauschung P zweier Teilchen sein:

$\psi(\vec r_1,s_1;\ldots,\vec r_n,s_n)=-(P \psi)(\vec r_1, s_1;\ldots,\vec r_n,s_n)\,\,.\qquad (1)$

Dabei sind 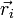$\vec r_i$ der Ort, s_i der Spin des i-ten Fermions und P der Permutationsoperator, der die Vertauschung jeweils zweier Teilchen bewirkt, also z. B.

$(P\psi)(\vec r_1,s_1;\vec r_2,s_2;\dots )\,:=\psi (\vec r_2,s_2;\vec r_1,s_1;\dots )\,\,.$

Ableitung

Sind zwei Teilchen ununterscheidbar, muss das Betragsquadrat der Wellenfunktion gegenüber der Vertauschung invariant sein:

$\left|\Psi\left(1,2\right)\right|^{2} = \left|\Psi\left(2,1\right)\right|^{2}$.

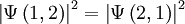Somit beschränkt sich die Wirkung des Permutationsoperators auf die Änderung des komplexen Anteils der Wellenfunktion und die Vertauschung der Teilchen:

$P\Psi\left(1,2\right) = e^{i\phi}\Psi\left(2,1\right)$.

Weitere Anwendung des Permutationsoperators macht die Vertauschung rückgängig:

$P^{2}\Psi\left(1,2\right) = PP\Psi\left(1,2\right) = Pe^{i\phi}\Psi\left(2,1\right) = e^{2i\phi}\Psi\left(1,2\right)$.

Um das Betragsquadrat konstant zu halten muss also gelten:

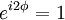$\!\,e^{ i 2\phi } = 1$ und $e^{i\phi} = \pm1$.

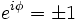Somit kann man zwischen zwei Sorten Teilchen unterscheiden, solchen bei denen sich unter Permutation das Vorzeichen der Wellenfunktion ändert (Fermionen), und solchen, bei denen sich das Vorzeichen der Wellenfunktion unter Permutation nicht ändert (Bosonen).

Anschauliche Deutung

Betrachtet man ein System aus zwei nichtunterscheidbaren Fermionen, so gilt wegen der Antisymmetrie der Gesamtwellenfunktion

$\psi(\vec r_1,s_1;\vec r_2,s_2)=-\psi(\vec r_2,s_2;\vec r_1,s_1).$

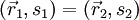Für $(\vec r_1,s_1)=(\vec r_2,s_2)$ ergibt sich daraus 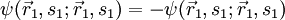$\psi(\vec r_1,s_1;\vec r_1,s_1)=-\psi(\vec r_1,s_1;\vec r_1,s_1)$, d.h. 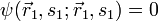$\psi(\vec r_1,s_1;\vec r_1,s_1)=0$. Die Wahrscheinlichkeit(sdichte) dafür, dass man bei einer Messung beide Fermionen am selben Ort 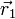$\vec r_1$ mit selbem Spin 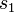$\!\,s_1$ findet, ist also Null.

In vielen Fällen (ein solcher Fall ist z.B. für nichtentartete Eigenfunktionen von Hamilton-Operatoren ohne Spin-Bahn-Kopplung stets gegeben) ist die Gesamtwellenfunktion 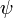$\!\,\psi$ als Produkt von Ortswellenfunktion 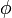$\!\,\phi$ und Spinwellenfunktion 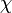$\!\,\chi$ darstellbar, also

$\psi(\vec r_1,s_1;\vec r_2,s_2)=\phi(\vec r_1,\vec r_2)\chi(s_1,s_2).$

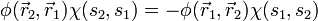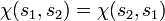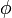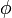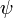Wegen der Antisymmetrie ist dann $\phi(\vec r_2,\vec r_1)\chi(s_2,s_1)=-\phi(\vec r_1,\vec r_2)\chi(s_1,s_2)$. Ist etwa die Spinwellenfunktion symmetrisch, also $\chi(s_1,s_2)\!\,=\chi(s_2,s_1)$, so folgt daraus die Antisymmetrie der Ortswellenfunktion $\!\,\phi$. Entsprechend gilt allgemein, dass die Symmetrie einer der Funktionen $\!\,\phi$ oder $\!\,\psi$ äquivalent zur Antisymmetrie der jeweils anderen ist. 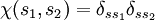Sind also die zwei Fermionen etwa im selben Spinzustand $\!\,s$, dann ist $\chi(s_1,s_2)=\delta_{ss_1}\delta_{ss_2}$ symmetrisch und daher folgt die Antisymmetrie der Ortswellenfunktion.

Diese Zusammenhänge gelten sinngemäß auch dann, wenn mehr als zwei nichtunterscheidbare Fermionen beteiligt sind.

Gültigkeit

Das Pauli-Prinzip gilt für alle Fermionen (Teilchen mit halbzahligem Spin). Diese genügen der Fermi-Dirac-Statistik aufgrund des sogenannten Spin-Statistik-Theorems.

Neben Fermionen gibt es auch Teilchen mit ganzzahligem Spin. Für diese so genannten Bosonen gilt das Pauli-Prinzip nicht. Präziser gesagt: es gilt mit der Änderung, dass in Gleichung (1) der Ausdruck − (Pψ...) durch + (Pψ...) zu ersetzen ist. Diese Teilchen genügen damit der Bose-Einstein-Statistik und können gleiche Quantenzustände einnehmen (im Extremfall bis zum Bose-Einstein-Kondensat).

Kurz zusammengefasst: Die Gesamtwellenfunktion ψ muss für Fermionen antisymmetrisch und für Bosonen symmetrisch sein.

Nur bei zweidimensionaler Geometrie sind auch Teilchen mit beliebiger Phase, sog. Anyonen, möglich.

Permutations- und Drehverhalten

Das unterschiedliche Permutationsverhalten von Fermionen und Bosonen passt genau zum unterschiedlichen Drehverhalten der jeweiligen Spinoren. In beiden Fällen ergibt sich ein Faktor von 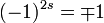$(-1)^{2s}=\mp 1$, mit dem (+)-Zeichen für Bosonen (s ganzzahlig) und dem (-)-Zeichen für Fermionen (s halbzahlig), entsprechend einer Drehung um 360^o. Der Zusammenhang ist u. a. deshalb naheliegend, weil eine Vertauschung der Teilchen 1 und 2 in der Tat einer komplementären Drehung der beiden Teilchen um 180⁰ entspricht (z. B. Teilchen 1 zum Ort 2 auf dem oberen Halbkreis, Teilchen 2 zum Ort 1 auf dem unteren Halbkreis).

Konsequenzen

Das Pauli-Prinzip führt zur Austauschwechselwirkung und ist für die Spinordnung in Atomen (Hundsche Regeln) und Festkörpern (Magnetismus) verantwortlich.

In der Astrophysik wird durch das Pauli-Prinzip erklärt, dass alte Sterne mit Ausnahme der sog. Schwarzen Löcher – zum Beispiel Weiße Zwerge oder Neutronensterne – nicht unter ihrer eigenen Gravitation zusammenbrechen. Hierbei erzeugen die Fermionen einen Gegendruck, der einer weiteren Kontraktion entgegenwirkt.

Siehe auch

Ununterscheidbare Teilchen, Fermion, Pauli-Matrizen