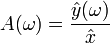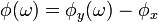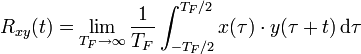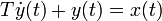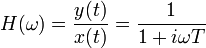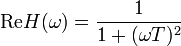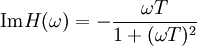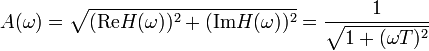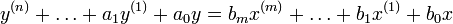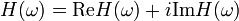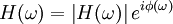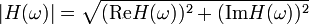- Frequenzkurve
-
Der Frequenzgang beschreibt das Verhalten eines linearen zeitinvarianten Systems in Abhängigkeit von der Frequenz; etwa bei einem Lautsprecher oder einem Filter in der Analogtechnik. Er ist eine komplexe Funktion der Frequenz.
Zur Ermittlung des Frequenzgangs wird das System mit einer sinusförmigen Eingangsgröße und variabler Frequenz angeregt. Die Ausgangsgröße des Systems ist ebenfalls wieder sinusförmig mit gleicher Kreisfrequenz, jedoch mit einer anderen Amplitude und einer Phasenverschiebung gegenüber dem Eingangssignal. Das Ergebnis dieses Versuchs wird über der Frequenz für das jeweilige Amplitudenverhältnis und die jeweilige Phasenlage aufgetragen. Sie werden als Amplitudengang (Betragsfrequenzgang) bzw. als Phasengang (Phasenfrequenzgang) bezeichnet. Die kombinierte Darstellung ist das Bode-Diagramm. Wird der Frequenzgang durch Realteil und Imaginärteil über der Frequenz als Laufvariable dargestellt, entsteht die Ortskurve.
Inhaltsverzeichnis
Experimentelle Ermittlung
Ein LZI-System mit einem harmonischen Eingangssignal
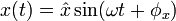 hat wiederum ein harmonisches Ausgangssignal. Auf Grund der Linearität wird die Frequenz
hat wiederum ein harmonisches Ausgangssignal. Auf Grund der Linearität wird die Frequenz  nicht beeinflusst. Lediglich die Amplitude
nicht beeinflusst. Lediglich die Amplitude  und die Phase
und die Phase  werden verändert und das Ausgangssignal ist
werden verändert und das Ausgangssignal ist 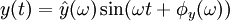 . Das Verhältnis
. Das Verhältnisist der Amplitudengang. Der Phasengang ist die Phasendifferenz
mit
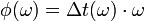 wobei
wobei 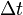 die gemessene Zeitverschiebung zwischen Ein- und Ausgangssignal der Frequenz ω ist, also
die gemessene Zeitverschiebung zwischen Ein- und Ausgangssignal der Frequenz ω ist, also 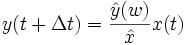 . Die Zeitverschiebung kann unter anderem durch Kreuzkorrelation
. Die Zeitverschiebung kann unter anderem durch Kreuzkorrelationbestimmt werden. Die Zeit
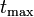 , bei der eine Spitze in
, bei der eine Spitze in 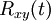 auftritt, ist die Zeitverschiebung zwischen Ein- und Ausgangssignal.
auftritt, ist die Zeitverschiebung zwischen Ein- und Ausgangssignal.Die Bestimmung des Frequenzganges erfolgt in der Praxis meistens mit Wobbelgeneratoren.
Beispiel
Die Differenzialgleichung des PT1-Gliedes ist
Mit dem Eingangssignal
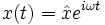 und dem Ausgangssignal
und dem Ausgangssignal 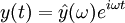 in komplexer Darstellung erhält man durch einsetzen in die DGL
in komplexer Darstellung erhält man durch einsetzen in die DGLden Frequenzgang. Der mit dem Realteil
und dem Imaginärteil
des Frequenzgangs gebildete Amplitudengang ist
und der Phasengang
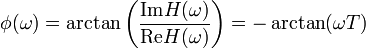 .
.
In der oberen Abbildung sind beide für T=0.1 s mit den gemessenen Werten dargestellt.
Allgemeine Herleitung
Lineare, zeitinvariante Systeme werden durch die lineare Differentialgleichung n-ter Ordnung
beschrieben. Die Anwendung der Fourier-Transformation auf die DGL ergibt den Frequenzgang
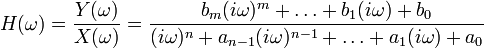 .
.
Die Anwendung der Fourier-Transformation ist gleich der Anregung des Systems mit einem kontinuierlichen Frequenzspektrum.
Darstellungen des Frequenzgangs:
- durch Real- und Imaginärteil
- durch Betrag und Phase
mit Betrag
und Phase
Die Fourier-Rücktransformierte des Frequenzganges ist die Gewichtsfunktion oder Impulsantwort:
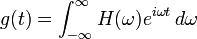 .
.
Literatur
- Heinz Unbehauen: Regelungstechnik I, Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, 1997, ISBN 3-528-83332-7
Weblinks
Wikimedia Foundation.