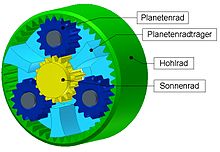
Planetengetriebe

Ein Planetengetriebe (manchmal auch Planetenradgetriebe genannt) ist eine spezielle Bauform eines kompakt bauenden Zahnrad-Getriebes. Charakteristisch sind die drei koaxial angeordneten Wellen.

Einfaches Planetengetriebe.

Prinzip Planetengetriebe

Grundlegender Aufbau

zu Illustrationszwecken vereinfachtes Planetengetriebe mit 2 Planetenrädern, üblich sind 3 oder mehr;

• Sonnenrad
• Planetenräder
• Hohlrad

Ein Planetengetriebe umfasst zwei Wellen und einen Planetenträger (auch Steg genannt). Es sind unterschiedliche Bauformen möglich, die sich im inneren Aufbau unterscheiden.

Die einfachste Bauart eines Planetengetriebes besteht aus einem Zahnradsatz, der von innen nach außen aus dem Sonnenrad, den von dem Planetenträger getragenen Planetenrädern und dem Hohlrad mit Innenverzahnung besteht. Prinzipiell sind verschiedene Funktionsweisen möglich. Bei dem hier gezeigten Aufbau sind alle Achsen raumfest (siehe Illustration rechts). Das grüne Sonnenrad wird angetrieben, was zu einer Drehung des roten Hohlrades führt. Die blauen Planetenräder drehen sich nicht um das grüne Sonnenrad. Bei einer anderen (hier nicht gezeigten) Realisierung wird das Hohlrad festgehalten und die Achsen der Planetenräder drehen sich um das Sonnenrad. Der Träger der Planetenradachsen wird angetrieben. Welches Rad als Antrieb und welches als Abtrieb dient, kann konstruktionstechnisch festgelegt werden.

Andere, komplexere Bauformen von Planetengetrieben können abweichend aufgebaut sein und beispielsweise zwei Sonnenräder, untereinander kämmende Planetenradpaare oder gestufte Planetenräder umfassen. Durch den anderen Aufbau können sich konstruktive Vorteile ergeben, zudem können Übersetzungsverhältnisse realisiert werden, die mit einem einfachen Planetenradsatz nicht darstellbar sind.

Betriebsarten

Planetengetriebe können im Zweiwellenbetrieb und im Dreiwellenbetrieb arbeiten:

Zweiwellenbetrieb

Im Zweiwellenbetrieb hat das Getriebe einen Freiheitsgrad von F = 1 – jede Bewegung ist eindeutig bestimmbar. Außerdem unterscheidet man den Zweiwellenbetrieb noch einmal in Standübersetzung und Umlaufübersetzung:

• Bei der Standübersetzung steht die Stegwelle still und die beiden Zentralradwellen (also Sonnen- und Hohlrad) bewegen sich. Die ruhende Welle wird entweder durch eine Bremse festgehalten oder ist fest mit dem Gehäuse verbunden.
• Bei der Umlaufübersetzung steht eine der beiden Zentralradwellen still. An- und Abtrieb erfolgen über eine Zentralradwelle und die Stegwelle.

Dreiwellenbetrieb

Im Dreiwellenbetrieb hat das Getriebe einen Freiheitsgrad von F = 2. Bei drei laufenden Wellen arbeitet das Getriebe als Summiergetriebe oder Teilergetriebe:

• Beim Summiergetriebe treiben 2 Wellen an und 1 Welle ab. Die Antriebsdrehzahlen können frei gewählt werden. Die Abtriebsdrehzahl wird durch die beiden Antriebsdrehzahlen eindeutig bestimmt.
• Beim Teilergetriebe treibt eine Welle an und zwei Wellen treiben ab. Das Drehzahlverhältnis der beiden Abtriebswellen muss festgelegt sein. Das bekannteste Beispiel eines Teilergetriebes ist das Differential am Kraftfahrzeug. Hier wird das Drehzahlverhältnis durch den Radabstand und den Kurvenradius festgelegt.

Mehrfachgetriebe

Oft wird nicht nur der hier geschilderte einfache Planetensatz als Planetengetriebe bezeichnet, sondern auch alle auf dieser Grundbauform beruhenden Kombinationen mehrerer, hintereinander geschalteter Planetensätze. Auf diese Weise lassen sich über mehrere (angetriebene) Wellen auch mehr Gänge oder Verzweigungen auf mehrere Abtriebe realisieren.

Kinematik

Mehrere axial hintereinander angeordnete Planetengetriebe in einer Fahrradnabe mit 14 Gängen (Speedhub 500/14)

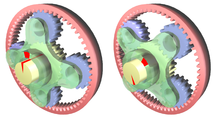In diesem Falle wird das Planetengetriebe zum Steigern der Ausgangsgeschwindigkeit verwendet:

• Der Planetenträger wird angetrieben,
• das Sonnenrad liefert das Ausgangsdrehmoment,
• das Hohlrad ist fest.
• Die roten Markierungen bezeichnen die Bewegung bei einer Drehung des angetriebenen Rades um 45° im Uhrzeigersinn
• Planetenräder

Fahrzeug mit Planetengetrieben an der Zwillingsachse: An diesem Militärlastwagen von Magirus-Deutz erkennbar an den nach außen gewölbten Abdeckungen der äußeren Planetenachsen

Charakteristisch für Planetengetriebe ist die Standübersetzung i₁₂, mit der Planetengetriebe unterschiedlichster Bauarten verglichen werden können. Wenn zwei Planetengetriebe gleicher Bauart die gleiche Standübersetzung haben, sind sie kinematisch gleichwertig. Alle anderen Übersetzungen sind dann ebenfalls gleich.

Zwischen der Standübersetzung i₁₂ und den Drehzahlen n von Sonnen-, Steg- und Hohlradwelle besteht der folgende mathematische Zusammenhang:

$i_{12}=\frac{n_{\mathrm{Sonnenrad}}-n_{\mathrm{Steg}}}{n_{\mathrm{Hohlrad}}-n_{\mathrm{Steg}}}=\frac{n_1-n_s}{n_2-n_s}$

Nach Umstellung ergibt sich die Willisgleichung:

$n_1-n_2 \cdot i_{12}-n_s \cdot (1-i_{12})=0$

Die Standübersetzung ist anschaulich deutbar als die Übersetzung von Hohlradwelle zur Sonnenradwelle bei festgehaltenem Steg (Fall n_Steg = 0). Sie ist negativ, wenn bei Antrieb eines Rades das andere entgegengesetzt dreht. Da man bei der Berechnung von i das Verhältnis von großem zu kleinem Rad ebenso wie das Verhältnis von kleinem zu großem Rad als i angeben kann, wird i stets so gewählt, dass es betragsmäßig größer als 1 wird.

Die Bedeutung der Standübersetzung kann man sich mit einer Erklärung anschaulich machen: Jeder Bewegungszustand des Planetengetriebes lässt sich darstellen, wenn man sich die Bewegung aus der Standübersetzung i mit festgehaltenem Steg vorstellt und sich dann vergegenwärtigt, dass danach auch noch der Steg gedreht werden kann.

Die Standübersetzung lässt sich durch die Zähnezahlen S und H von Sonnenrad und Hohlrad berechnen:

$\qquad i_{12}=\frac{H}{S}$

Bei einem Hohlrad ist die Zähnezahl negativ definiert, so dass auch hier i negativ wird und die Drehrichtungsumkehr bei festgehaltenem Steg anzeigt. Die Zähnezahl der Planetenräder hat bei einem einfachen Planetenradsatz keinen Einfluss auf die Standübersetzung.

Bei einem Planetengetriebe sind alle Räder ständig im Eingriff. Durch die Wahl des Antriebes und des Abtriebes bzw. des Abbremsens oder Kuppelns kann die Übersetzung gewechselt werden.

Das Hohlrad weist eine Innenverzahnung auf. Zudem führt die Anzahl der Planetenräder zu einer Leistungsverzweigung. Diese beiden Merkmale bewirken, dass die mechanische Belastbarkeit des Getriebes gesteigert bzw. das Getriebe kleiner, kompakter gebaut werden kann. Zur Erzeugung eines Rückwärtsganges ist kein Rücklaufrad nötig.

Die Vorteile von Planetengetrieben gegenüber anderen Getriebebauarten zur Drehzahl- und Momentenumwandlung liegen einerseits in der Möglichkeit einer Änderung des Übersetzungsverhältnisses unter Last, d.h. ohne Unterbrechung des Kraftflusses, und anderseits in ihrer kompakten Größe bei vergleichbarer Übersetzung. Zudem sind koaxiale Richtungsumwandlungen möglich.

Anwendung

Am bekanntesten sind wegen der hohen Verbreitung Nabenschaltungen an Fahrrädern. Diese basieren überwiegend auf Planetengetrieben.

Untersetzungsgetriebe

Planetengetriebe ermöglichen große Übersetzungsstufen und große Drehmomente, da die mehrfachen Planeten die Leistung teilen und übertragen. Charakteristisch für solche Getriebe ist, dass sie nur einen Eingang und einen Ausgang haben, die koaxial liegen. Da sie dabei auch das Ausgangsmoment verändern, muss ein Teil des Getriebes festgehalten werden (Momentenstütze). Dazu gibt es vielfältige Anwendungsbeispiele:

In den Antriebsnaben von Lastkraftwagen, Omnibussen sowie in Bau- und Landmaschinen werden sie zur Untersetzung verwendet. Man spricht dann von sog. Außenplanetenachsen. Diese Technik wurde 1953 vom Nutzfahrzeughersteller Magirus-Deutz eingeführt und in der Folgezeit auch von zahlreichen anderen Herstellern übernommen. Außenplanetenachsen sind bei schweren Bau- und Allrad-Lkw heute noch Stand der Technik.

Achtgang-Stufenautomatgetriebe der Firma ZF-Getriebe AG vom Typ 8HP70. Die verschiedenen Gänge werden mit mehreren Planetengetrieben realisiert.

In der Regel werden in klassischen Automatikgetrieben für Kraftfahrzeuge mehrere hintereinandergeschaltete Planetengetriebe verwendet, zum Beispiel. einfache Planetenradgetriebe, Ravigneaux- oder Simpson-Satz. Zum Gangwechsel wird durch Öffnen und Schließen von Kupplungen und Bremsen eine andere Übersetzung geschaltet. Dies geschieht als Lastschaltung, es gibt keine Zugkraftunterbrechung.

Summiergetriebe

Bei einem Summiergetriebe werden zwei Leistungen zu einer zusammengefasst. Ein Beispiel dafür ist ein Schiffspropeller, der von zwei Motoren über ein Summiergetriebe angetrieben wird.

Im Pkw-Bereich wurden so auch Überlagerungsgetriebe vorgestellt, bei denen der Verbrennungsmotor und ein Elektromotor gemeinsam Antriebsleistung für einen Beschleunigungsvorgang liefern. Läuft der Elektromotor zunächst rückwärts, dann lässt sich sogar eine kupplungslose Anfahrregelung darstellen. Auch lassen sich stufenlose Lenkübersetzungen emulieren, wenn ein Elektromotor über ein Summiergetriebe der Lenkradbewegung überlagert wird (z.B. bei BMW).

Andere Anwendungen haben einen Motor, der große Leistungen bei konstanter Drehzahl liefert. Mit einem kleineren Motor, der sich leicht in der Drehzahl regeln lässt, und einem Summiergetriebe kann auf diese Art in einem kleinen Bereich eine Drehzahländerung am Ausgang erreicht werden. Einsatzbereich wären z. B. Walzwerke, um die Geschwindigkeiten bei der Umformung zu regeln.

Im Flugzeugbau sind Anwendungen bekannt, bei denen aus Sicherheitsgründen zwei Elektromotoren eine Kraftstoffpumpe über ein Summiergetriebe antreiben. Fällt einer der Motoren aus, kann der andere immer noch die Pumpe antreiben, wenngleich sich die Gesamtleistung halbiert.

Leistungsverzweigung

Klassischer Anwendungsfall für leistungsverzweigende Planetengetriebe werden in Verteilergetrieben bei Allradfahrzeugen (Zentraldifferenzial, siehe Differentialgetriebe) und in den Achsgetrieben als Achsdifferenzial verwendet. Ebenso in Hybridelektrokraftfahrzeugen, wo das Planetengetriebe die Leistung zwischen Verbrennungsmotor, Elektromotor und Generator verzweigt.

Als Kupplung

Vorwiegend in der Landtechnik werden Planetengetriebe als weich schaltbare Kupplung eingesetzt, beispielsweise um die Drehzahl einer Zapfwelle zu variieren oder zu schalten. Hierbei wird das Antriebsdrehmoment des Antriebsmotors kontinuierlich zum Sonnenrad geliefert, das Abtriebsdrehmoment wird vom Planetenträger über das Hohlrad auf die Zapfwelle übertragen.

Ist das Hohlrad frei drehend gestaltet kann kein Drehmoment vom Sonnenrad auf den Planetenträger und somit auch nicht auf die Zapfwelle übertragen werden.

Wird das Hohlrad beispielsweise durch eine Bandbremse durch das erzeugte Drehmoment in der freien Drehung gehindert oder auch angehalten, kann das Drehmoment vom Sonnenrad über das Hohlrad auf den Planetenträger übertragen werden.

Bei Kompressionsdrehriegeln

Durch Planetengetriebe wird bei den in industriellen Gehäusen üblichen Drehriegelverschlüssen ein vergrößerter Kompressionshub ermöglicht. Gleichzeitig kann der Anpressdruck vergrößert werden. Kennzeichnend ist das kleine von Hand aufzubringende Drehmoment.

Andere Anwendungen

Mit Kombinationen von Planetengetrieben lässt sich auch der Leistungsbereich von stufenlosen Getrieben erweitern (allerdings bei reduziertem Drehzahlband). Zunächst wird die Antriebsleistung mit einem Planetengetriebe aufgeteilt. Ein Nebenzweig mit geringerer Leistung wird über ein stufenloses Getriebe zu einem zweiten Planetengetriebe geführt, wo es dann mit der Leistung aus dem Hauptzweig des ersten Planetengetriebes wieder summiert wird.

Berechnung

Die Berechnung ist mit dem Kutzbachplan möglich.

Folgende Übersetzungen sind möglich:

Hohlrad fest		Sonnenrad fest		Planetenradträger fest
Antrieb / Abtrieb	Übersetzung	Antrieb / Abtrieb	Übersetzung	Antrieb / Abtrieb	Übersetzung
Planetenradträger / Sonnenrad	$i = \frac 1 {1- i_{12}}$	Hohlrad / Planetenradträger	$i = 1- \frac {1} {i_{12}}$	Sonnenrad / Hohlrad	i = i12
Sonnenrad / Planetenradträger	i = 1 − i12	Planetenradträger / Hohlrad	$i = \frac 1 {1- \frac {1} {i_{12}}}$	Hohlrad / Sonnenrad	$i = \frac {1} {i_{12}}$

(Anmerkung: Die Übersetzungen der letzten Tabellenzeile sind reziprok zu ihrer Entsprechung in der vorletzten Tabellenzeile, weil hier nur die Positionen von An- und Abtrieb vertauscht sind.)

Standübersetzung $i_{12}=\frac {z_H}{z_S}$ (bei einem einfachen Planetenradsatz negativ)

z_H = Zähnezahl Hohlrad (negativ); z_S = Zähnezahl Sonnenrad

Stufenloses NuVinci-Getriebe

Sein Grundprinzip wurde bereits von Leonardo da Vinci beschrieben. Der Name NuVinci ist davon abgeleitet. Es handelt sich um ein stufenloses Planetengetriebe, in dem der Kraftschluss durch Kugeln erfolgt. Durch Kippen dieser Kugeln in Verhältnis zu den seitlichen angeordneten Scheiben kann das Übersetzungsverhältnis stufenlos variiert werden. Fahrradnaben der Firma Fallbrook funktionieren nach diesem Prinzip und weisen eine Getriebespreizung von bis zu 360% auf.^[1]

Anhang

Literatur

• Hugo Klein: Die Planetenrad-Umlaufrädergetriebe, Carl Hanser Verlag München, 1952.
• Fritz Winkler, Siegfried Rauch: Fahrradtechnik Instandsetzung, Konstruktion, Fertigung. 10. Auflage, BVA Bielefelder Verlagsanstalt GmbH & Co. KG, Bielefeld, 1999, ISBN 3-87073-131-1
• Johannes Volmer: Getriebetechnik Umlaufrädergetriebe, Verlag Technik, Berlin, 1990

Einzelnachweise

1. ↑ NuVinci: Datenblatt des NuVinci N360 CVP (pdf)

Weblinks

 Commons: Planetary gearing – Sammlung von Bildern, Videos und Audiodateien

• Planetengetriebe in der Kfz-Technik bei www.kfz-tech.de
• Verwandtschaft zwischen Planetengetrieben und Differenzialen bei www.arstechnica.de

Siehe auch

• Planetenrollengewindetriebe in der Lineartechnik