- Projektion (Geometrie)
-
Projektion ist in der Geometrie eine Abbildung, die Punkte des dreidimensionalen Raumes auf Punkte einer gegebenen Ebene abbildet. Eine Projektion dient häufig dazu, Schrägbilder von geometrischen Körpern herzustellen. Man unterscheidet zwei Grundtypen, die Parallelprojektion und die Zentralprojektion. Die Abbildung auf die Bildebene kann sowohl grafisch mittels gezeichneter Hilfskonstruktionen (Verfahren der darstellenden Geometrie) als auch mathematisch (meist computergestützt, dreidimensionales CAD) erzeugt werden.
Inhaltsverzeichnis
Parallelprojektion
Bei der Parallelprojektion, auch Orthografische Projektion oder Orthoprojektion, sind eine Projektionsebene und eine Projektionsrichtung gegeben. Den Bildpunkt eines beliebigen Punktes im Raum erhält man dadurch, dass man die Parallele zur Projektionsrichtung durch diesen Punkt mit der Projektionsebene zum Schnitt bringt.
Geraden werden durch eine Parallelprojektion im Allgemeinen wieder auf Geraden abgebildet. Das gilt jedoch nicht für Parallelen zur Projektionsrichtung, da diese in Punkte übergehen. Die Bildgeraden von parallelen Geraden sind - soweit definiert - ebenfalls parallel zueinander. Die Länge einer Strecke bleibt nur dann erhalten, wenn diese parallel zur Projektionsebene verläuft; in allen anderen Fällen erscheinen Strecken in der Projektion verkürzt. Auch die Größe eines projizierten Winkels stimmt normalerweise nicht mit der Größe des ursprünglichen Winkels überein. Aus diesem Grund wird ein Rechteck im Allgemeinen auf ein Parallelogramm abgebildet, aber nur in Ausnahmefällen auf ein Rechteck. Ähnliches gilt für Kreise, die im Allgemeinen in Ellipsen übergehen.
Ein wichtiger Spezialfall ist die orthogonale (senkrechte) Parallelprojektion. Sie ist dadurch gekennzeichnet, dass Projektionsrichtung und Projektionsebene zueinander senkrecht sind. Die orthogonale Parallelprojektion entspricht einer Fotografie mit einem telezentrischen Objektiv oder (näherungsweise) mit einem starken Teleobjektiv.
Berechnung von Bildpunkten
Soll ein Punkt P auf eine Ebene
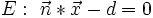 mittels einer Parallelprojektion mit der Projektionsrichtung
mittels einer Parallelprojektion mit der Projektionsrichtung 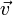 abgebildet werden, so ist der Bildpunkt von P der Schnittpunkt der Geraden g durch P mit dem Richtungsvektor
abgebildet werden, so ist der Bildpunkt von P der Schnittpunkt der Geraden g durch P mit dem Richtungsvektor 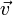 .
.
Lässt man Ebene und Gerade schneiden, so ergibt sich für den Parameter λ:
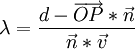
Setzt man diesen in die Gerade g ein, so erhält man den Schnittpunkt dieser mit E und damit den Bildpunkt P'.
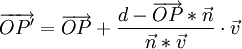
Um die Projektion mit einer Matrixmultiplikation darstellen zu können, sind folgende Umformungen nötig:
Eine Abbildung, welche eine Projektion eines beliebigen Raumes auf einen echten Unterraum darstellt, erhält man über das Matrizenprodukt der Matrix, welche aus einer Orthonormalbasis des Raumes besteht, mit sich selber:
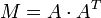
Eine Projektion auf den komplementären Unterraum erhält man mit
M' = I − M
Benutzt man nun den Normalenvektor (Ein Raum der Dimension 1) der Ebene von oben, und projiziert auf den Komplementärraum, so projiziert man im R3 auf eine Ebene - die Projektionsebene.
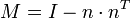
Da damit nur Projektionen auf Unterräume, nicht aber auf affine Unterräume möglich sind, muss man, bevor man projiziert, den zu projizierenden affinen Raum auf den Ursprung verschieben und danach eine Rücktranslation durchführen.

Zentralprojektion (Fluchtpunktverfahren)
- Hauptartikel Zentralprojektion
Das Verfahren, welches in der Praxis zur Geltung kommt, macht sich zu Nutze, wie unser Gesichtssinn arbeitet: Ein Punkt in der Ferne wird fixiert, und die dreidimensionale Wirkung ergibt sich dadurch, dass weiter entfernte Punkte in ihren X- und Y- Koordinatenanteilen näher an diesen Fluchtpunkt heranrücken. Das bedeutet: Bei der Darstellung dreidimensionaler Objekte beispielsweise auf einem Computerbildschirm müssen erst die Koordinaten absolut definiert werden, und dann mittels Fluchtlinien auf der Ebene dargestellt werden.
Berechnung von Bildpunkten
Die Berechnung der Verschiebung um die x-Achse und die y-Achse entlang der Fluchtlinien findet mithilfe der Strahlensätze statt.
Es sei P = (Px,Py,Pz)T der Punkt, dargestellt als dreidimensionaler Vektor, Q = (Qx,Qy,Qz)T der Fluchtpunkt und R = (Rx,Ry)T die zu berechnenden Koordinaten im zweidimensionalen Raum. Dann ist
und dementsprechend
 .
.In Matrixschreibweise lassen sich die obigen Formeln dann folgendermaßen zusammenfassen (mit homogener Erweiterung, d.h. P = (Px,Py,Pz,1)T, R' = (Rx,Ry,0,Rw)T und
 ):
):

Anwendungen
Siehe auch
- Dreitafelprojektion
- Orthografische Azimutalprojektion
- Kartenprojektion
- engl. Wikipedia „3D projection“ (engl.)
Wikilinks
Wikimedia Foundation.


