Orthografische Projektion

Die Artikel Zentralprojektion und Gnomonische Projektion überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Analemma 21:18, 20. Apr. 2009 (CEST)

Prinzip der Zentralprojektion

Die Zentralprojektion ist ein Verfahren zur perspektivischen Abbildung dreidimensionaler Objekte auf eine zweidimensionale Bildebene. Die Projektionsstrahlen schneiden sich in einem Punkt, dem Projektionszentrum. Geraden werden als Geraden abgebildet. Parallele Geraden des Raumes schneiden sich im Bild in einem gemeinsamen Fluchtpunkt. Die Zentralprojektion entspricht der Abbildung durch das menschliche Auge und ergibt somit einen natürlichen Bildeindruck. In der darstellenden Geometrie, der Architektur und der darstellenden Kunst wird die Zentralprojektionen zur Darstellung in Zentralperspektive, Vogelperspektive und Froschperspektive genutzt. In der Kartografie wird die Zentralprojektion für den Entwurf von Kartennetzen verwendet.

Ein Spezialfall der Zentralprojektion ist die Parallelprojektion (Parallelriss) . Bei dieser liegt das Projektionszentrum unendlich weit entfernt. Die Projektionsstrahlen verlaufen deshalb parallel.

Prinzip

Funktionsweise einer Lochkamera

Unser einäugiges Sehen arbeitet ebenso nach dem Prinzip der Zentralprojektion, wie die einfache Lochkamera.

Das abzubildende Objekt, im Beispiel oben rechts die zwei sich schneidenden Dreiecke P1, P2, P3 und Q1, Q2, Q3, wird von einem in endlicher Entfernung liegenden Projektionszentrum „O“, wie der Irisblende des menschlichen Auges oder der Lochblende der Kamera, durch die Projektionsstrahlen (Lichtstrahlen) auf eine Bildebene, wie die Netzhaut oder einen fotografischen Film, projiziert.

In der Prinzipskizze liegt die Bildebene zwischen Objekt und Projektionszentrum. Beim Auge und der Kamera liegt sie dahinter: die Projektionsstrahlen werden dazu über das Projektionszentrum hinaus verlängert. Das Bild wird dadurch umgekehrt.

Wenn die Bildebene vom Projektionszentrum weg verschoben wird, vergrößert sich die Abbildung maßstabsgerecht. Wird der Abstand zwischen Bildebene und Projektionszentrum verkleinert, so wird auch die Abbildung verkleinert. Die Gerade, die senkrecht auf der Bildebene steht und gleichzeitig durch das Projektionszentrum O geht, ist die Bildachse. Auf der Bildachse ist das Bild unverzerrt. Je weiter sich ein Bildpunkt vom Durchstoßpunkt dieser Geraden durch die Bildebene entfernt, desto größer wird die Verzerrung. Sind die Objektebene und die Bildebene nicht parallel, so ist die Verzerrung nicht nur radiusabhängig sondern auch richtungsabhängig verschieden.

Für die allgemeine Zentralprojektion gelten folgende Sätze:

• Jeder Raumpunkt hat einen eindeutig zugeordneten Bildpunkt P'
• Jeder Bildpunkt P' ist das Bild unendlich vieler Raumpunkte P, die alle auf dem Projektionsstrahl durch P' liegen
• Eine Gerade wird wieder als Gerade abgebildet.
• Die Bilder aller Projektionsstrahlen schneiden sich in einem Punkt, dem Bildhauptpunkt H'
• Die Bilder paralleler Geraden schneiden sich in einem gemeinsamen Fluchtpunkt F'
• Figuren, die in einer Ebene parallel zur Bildebene liegen werden ähnlich abgebildet. Winkel deren Schenkel parallel zur Bildebene liegen werden daher getreu abgebildet
• Das Doppelverhältnis von vier auf einer Geraden liegenden Punkte bleibt erhalten

Typische Anwendungen der Zentralprojektion finden wir auch

• in der Fotografie z. B. beim Entzerren von Schrägaufnahmen,
• in der Photogrammetrie z. B. bei der Auswertung und Ausmessung von (Luft-) Bildern
• in der Darstellenden Geometrie und der Architektur bei der perspektivischen zeichnerischen Darstellung von Objekten
• in Kartografie für Kartennetzentwürfe (gnomonische Projektion; stereografische Projektion)
• in der Gnomonik der Lehre von der Sonnenuhr zur Abbildung der Sonne auf ein Zifferblatt

Parallelprojektion

Prinzip der Parallelprojektion

Wenn das Projektionszentrum unendlich weit entfernt ist, dann verlaufen die Projektionsstrahlen parallel. Diese Sonderform der Zentralprojektion wird Parallelprojektion genannt. Wenn wir Schattenspiele mit der (angenähert) unendlich weit entfernten Sonne machen, so sind die Schatten Parallelprojektionen. Auch hier gibt es Verzerrungen, wenn die Projektionsfläche nicht senkrecht zur Verbindungslinie Sonne (=Projektionszentrum) und senkrecht zum Objekt steht.

Wenn die Projektionsstrahlen schräg auf die Bildebene treffen handelt es sich um die allgemeine (auch: schiefe) Parallelprojektion. Für die allgemeine Parallelprojektion gelten folgende Sätze:

• Jeder Raumpunkt hat einen eindeutig zugeordneten Bildpunkt P'
• Jeder Bildpunkt P' ist das Bild unendlich vieler Raumpunkte P, die alle auf dem Projektionsstrahl durch P' liegen
• Eine Gerade wird wieder als Gerade abgebildet. Der Durchstoßpunkt einer Geraden durch die Bildebene wird Spurpunkt S' genannt
• Das Bild eines Projektionsstrahles ist sein Durchstoßpunkt S'
• Die Bilder paralleler Geraden sind ebenfalls einander parallel. (Geraden die parallel zur Bildebene und außerhalb derselben verlaufen haben kein Bild.
• Das Streckenverhältnis dreier auf der gleichen Geraden liegenden Punkte A, B, C bleibt im Bild erhalten:

$\overline{AB}:\overline{BC} = \overline{A'B'}:\overline{B'C'}$

• Strecken, Winkel und Figuren, die in einer Ebene parallel zur Bildebene liegen werden getreu wiedergegeben

Wenn die Bildebene senkrecht zu den Projektionsstrahlen steht, handelt es sich um die orthogonale Projektion (auch: Normalprojektion). Für den Fall einer orthogonalen Projektion gilt zusätzlich zu den Sätzen für den allgemeinen Fall:

• Rechte Winkel bleiben erhalten, wenn mindestens ein Schenkel parallel zur Bildebene ist und der zweite nicht in Projektionsrichtung zeigt.

Parallelprojektionen finden wir in Zeichnungen der Darstellenden Geometrie und der Architektur z.B. als Dreitafelprojektion. In der Kartografie wird sie als Orthografische Projektion bezeichnet und findet bei Kartennetzentwürfen Anwendung.

Berechnung von Bildpunkten

Mathematisch gesehen sind Zentralprojektionen so genannte projektive (kollineare) Abbildungen. Die Projektionsbeziehung zwischen Objektraum und Bildraum ist folglich eine räumliche Ähnlichkeitstransformation.

Zur numerischen Berechnung von Bildpunkten ebenso wie zur Rekonstruktion der Projektionsstrahlen der Zentralprojektion muss die räumliche Lage des Bündels der Projektionsstrahlen relativ zum Aufnahmeobjekt bekannt sein. Diese wird üblicherweise durch 6 Elemente bestimmt. Das sind drei Translationen (Lage des Projektionszentrums in x-, y- und z-Richtung eines objektbezogenen Koordinatensystems) und drei Rotationen welche die Drehung des Bildkoordinatensystems gegenüber dem Objektkoordinatensystem beschreiben. Dazu werden drei unabhängige Eulerwinkel z.B. die Neigung, die Kantung und der Richtungswinkel der Projektionsachse bevorzugt. Für die Festlegung des Abbildungsmaßstabes ist zusätzlich noch die Lage des Projektionszentrums im Bildkoordinatensystem erforderlich. Diese Art der numerischen Beschreibung kommt vor allem bei der Auswertung von Messbildern in der Photogrammetrie zum Einsatz und wird als Orientierung bezeichnet.

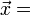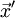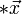Einfach und übersichtlich wird die Abbildungsgleichung der Zentralprojektion, wenn das Objekt sich in einer Ebene parallel zur Bildebene befindet und der Koordinatenursprung des Objektraumes wie auch des Bildraumes in das Projektionszentrum gelegt wurde. Dann gilt für den Ortsvektor $\vec x =$ {x₁,x₂,x₃} die Beziehung $\vec x'$= k $\ast\vec x$, wobei k ein Maßstabsfaktor ist. Er entspricht dem Verhältnis der vom Projektionszentrum O aus gemessenen Entfernung der Bildebene und der Objektebene. Diese einfache Abbildungsvorschrift ist in der unten gezeigten zeichnerischen Konstruktion einer zentralperspektivischen Abbildung erkennbar.

Die Abbildungsvorschrift für den allgemeinen Fall der Parallelprojektion erhält man so:

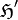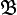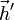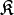Es sei $\mathfrak{H'}$ ein Raumpunkt in der Bildebene $\mathfrak{B}$ mit dem Ortsvektor $\vec h'$ und $\mathfrak{K}$ ein orthogonales Koordinatensystem mit den Einheitsvektoren 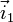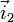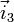$\vec i_1$;$\vec i_2$;$\vec i_3$ mit Ursprung in 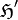$\mathfrak{H'}$ derart, dass 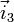$\vec i_3$ die Hauptnormale der Bildebene repräsentiert. Dann beschreibt das Skalarprodukt 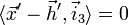$\langle\vec x'-\vec h',\vec i_3\rangle = 0$ die Bildebene 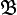$\mathfrak{B}$ in der Punkt-Normalenform und 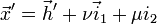$\vec x' = \vec h' + \nu \vec i_1 + \mu i_2$ beschreibt die Bildebene 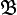$\mathfrak{B}$ in der Punktrichtungsform. Ist nun mit dem Richtungsvektor 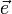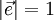$\vec e$ ; $|\vec e|=1$ die Projektionsrichtung gegeben, so beschreibt für einen beliebigen Raumpunkt 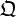$\mathfrak{Q}$ mit Ortsvektor 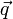$\vec q$ der Term 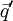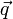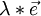$\vec q'$ = $\vec q$ + $\lambda\ast\vec e$ den Projektionsstrahl durch 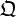$\mathfrak{Q}$ in der sogenannten Punktrichtungsform oder Vektorproduktform. Den Bildpunkt 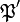$\mathfrak{P'}$ erhält man als Schnittpunkt der Projektionsgeraden mit der Bildebene durch Gleichsetzen der Geradengleichung mit der Ebenengleichung, wobei bevorzugt die Punktrichtungsformen verwendet werden. Zu beachten ist, dass nur dann eine Abbildung möglich ist, wenn für das Skalarprodukt 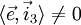$\langle \vec e,\vec i_3\rangle \ne 0$ gilt, mithin die Projektionsstrahlen nicht parallel zur Bildebene verlaufen.

Gilt für das Skalarprodukt der beiden Einheitsvektoren 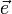$\vec e$ und $\vec i_3$:

$|\langle\vec e,\vec i_3\rangle| =1$,

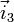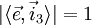d.h. der Normalenvektor der Bildebene und die Projektionsrichtung sind parallel, so handelt es sich um die orthogonale Parallelprojektion.

Anwendungen

Zentralperspektive

Die nebenstehende Grafik zeigt die Anwendung der Zentralprojektion zur perspektivischen Darstellung eines Gebäudes. Die Zentralperspektive wird unter anderem in der Architektur zur Verdeutlichung von Gebäudewirkung aber auch in der Malerei zum Aufbau eines Bildes mit Perspektive genutzt.

Das Projektionszentrum O entspricht der Position des Auges des Betrachters (Augpunkt). Parallele Geraden schneiden sich in einem gemeinsamen Fluchtpunkt F. Geraden die parallel zur Blickrichtung des Betrachters verlaufen, haben ihren Fluchtpunkt im Abbild des Augenpunktes. Parallele Ebenen schneiden sich in einer gemeinsamen Geraden. Bei der Zentralperspektive schneiden sich die waagerechten Ebenen im Horizont.

In der Abbildung ist erkennbar wie die perspektivische Darstellung aus Grundriss und Aufriss entwickelt werden kann. Aus der Projektion eines Objektpunktes im Aufriss auf die Bildebene B und im Grundriss auf die Bildebene B' ergeben sich horizontale und vertikale Schnittgeraden, in deren Schnittpunkt das perspektivische Bild des Objektpunktes liegt.

Bei diesem Beispiel sind alle vertikalen Geraden auch in der Projektion parallel: ihr Fluchtpunkt liegt im Unendlichen. Wird der Fluchtpunkt für diese Geraden ins Endliche verlegt, so erhält man stürzende Linien wie bei der Vogelperspektive oder der Froschperspektive.

Grundriss, Aufriss und Seitenriss der Dreitafelprojektion sind orthogonale Parallelprojektionen.

Weitere Anwendungen:

• Kartografie,
• Als fortlaufende Parallelprojektion seit 1822 für den Bildkartentypus des Rheinpanorama in Gebrauch.

Literatur

• Fritz Reinhardt / Heinrich Soeder: dtv-Atlas zur Mathematik, Tafel und Texte, Band I, Grundlagen, Algebra und Geometrie Deutscher Taschenbuch Verlag, München 1982
• W. Rüger, J. Pietschner, K. Regensburger: Photogrammetrie, Verfahren und Geräte, VEB Verlag für Bauwesen, Berlin 1978

Siehe auch

• Perspektive, Sehpyramide (Malerei), Projektion (Optik), Optische Messtechnik
• Axonometrie
• Koordinatentransformation
• Gnomonische Projektion
• Dreitafelprojektion
• Orthografische Azimutalprojektion
• Kartenprojektion
• engl. Wikipedia „3D projection“ (engl.)