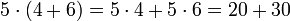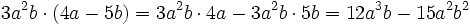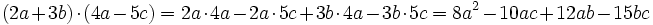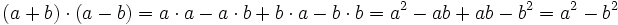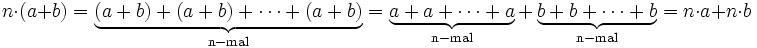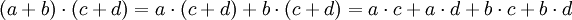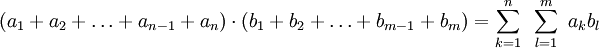Ausklammern — In der elementaren Algebra ist es häufig sinnvoll, Summen oder Differenzen in Produkte umzuwandeln. Dies gilt beispielsweise dann, wenn man einen Bruchterm durch Kürzen gemeinsamer Faktoren von Zähler und Nenner vereinfachen will. Eine wichtige… … Deutsch Wikipedia
Binomische Formeln — Die Binomischen Formeln sind in der elementaren Algebra verbreitete Formeln zur Darstellung und zum Lösen von Quadrat Binomen. Sie werden als Merkformeln verwendet, die zum einen das Ausmultiplizieren von Klammerausdrücken erleichtern, zum… … Deutsch Wikipedia
Binomische Gleichung — Die Binomischen Formeln sind in der elementaren Algebra verbreitete Formeln zur Darstellung und zum Lösen von Quadrat Binomen. Sie werden als Merkformeln verwendet, die zum einen das Ausmultiplizieren von Klammerausdrücken erleichtern, zum… … Deutsch Wikipedia
Faktorenzerlegung — In der elementaren Algebra ist es häufig sinnvoll, Summen oder Differenzen in Produkte umzuwandeln. Dies gilt beispielsweise dann, wenn man einen Bruchterm durch Kürzen gemeinsamer Faktoren von Zähler und Nenner vereinfachen will. Eine wichtige… … Deutsch Wikipedia
Kreiszahlberechnung nach Wallis — Das wallissche Produkt, auch Wallis Produkt, ist eine Produktdarstellung der Kreiszahl π, das heißt es handelt sich um ein Produkt mit unendlich vielen Faktoren, dessen Grenzwert Pi ist. Es wurde 1655 von dem englischen Mathematiker John Wallis… … Deutsch Wikipedia
Produktzerlegung — In der elementaren Algebra ist es häufig sinnvoll, Summen oder Differenzen in Produkte umzuwandeln. Dies gilt beispielsweise dann, wenn man einen Bruchterm durch Kürzen gemeinsamer Faktoren von Zähler und Nenner vereinfachen will. Eine wichtige… … Deutsch Wikipedia
Wallis-Produkt — Das wallissche Produkt, auch Wallis Produkt, ist eine Produktdarstellung der Kreiszahl π, das heißt es handelt sich um ein Produkt mit unendlich vielen Faktoren, dessen Grenzwert Pi ist. Es wurde 1655 von dem englischen Mathematiker John Wallis… … Deutsch Wikipedia
Wallissches Produkt — Das wallissche Produkt, auch Wallis Produkt, ist eine Produktdarstellung der Kreiszahl π, das heißt es handelt sich um ein Produkt mit unendlich vielen Faktoren, dessen Grenzwert Pi ist. Es wurde 1655 von dem englischen Mathematiker John Wallis… … Deutsch Wikipedia
Binomische Formel — Die Binomischen Formeln sind in der elementaren Algebra verbreitete Formeln zum Umformen von Produkten aus Binomen. Sie werden als Merkformeln verwendet, die zum einen das Ausmultiplizieren von Klammerausdrücken erleichtern, zum anderen erlauben… … Deutsch Wikipedia
Distributiv-Gesetz — Die Distributivgesetze (lat. distribuere „Verteilen“), auf Deutsch Verteilungsgesetze, sind mathematische Regeln und geben an, wie sich zwei zweistellige Verknüpfungen, zum Beispiel Multiplikation ( ) und Addition (+), bei der Auflösung von… … Deutsch Wikipedia