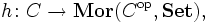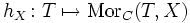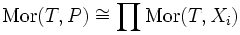- Natürliche Äquivalenz
-
Die Kategorientheorie oder die kategorielle Algebra ist ein Zweig der Mathematik, der sich Anfang der 1940er Jahre zuerst im Rahmen der Topologie entwickelte; Saunders MacLane nennt seine 1945 gemeinsam mit Samuel Eilenberg entstandene „General Theory of Natural Equivalences“ (in Trans. Amer. Math. Soc., 58, 1945) die erste explizit kategorientheoretische Arbeit. Die Grundbegriffe dieser Theorie sind Kategorie, Funktor und natürliche Transformation. Um den letzteren Begriff zu präzisieren, wurden die anderen eingeführt.
Die Kategorientheorie lässt sich, ähnlich wie die universelle Algebra, als allgemeine Theorie mathematischer Strukturen auffassen. Dabei werden allerdings Eigenschaften mathematischer Strukturen (klassische Strukturen sind z. B. Gruppen, Ringe, Moduln und topologische Räume) nicht über Relationen zwischen Elementen (der Trägermenge(n)) definiert, sondern gleichsam durch Vergleiche (mittels „Morphismen“ und „Funktoren“) sowohl innerhalb von als auch zwischen Kategorien.
Diese Art der Abstraktion führt nicht nur zu einer Klärung grundlegender, theorieübergreifender Begriffe, sie ermöglicht es auch, erfolgreiche Methoden und Konzepte einer speziellen mathematischen Theorie auf andere Bereiche und Objektklassen zu übertragen. Ein illustratives Beispiel liefert die Geschichte der homologischen Algebra, deren Methoden zuerst auf abelsche Gruppen beschränkt waren, dann auf Moduln über Ringen verallgemeinert wurden und schließlich, im kategorientheoretischen Gewand der Theorie der abelschen Kategorien, auf abelsche Garben übertragen wurden und da der Konstruktion von Kohomologietheorien, vor allem in der algebraischen Geometrie, dienen.
Die Kategorientheorie ist ebenso für Grundlagenfragen relevant. Topoi, das sind kategorientheoretische Extrakte der Kategorie der Mengen, in der wichtige Eigenschaften von Mengen rein pfeiltheoretisch formuliert werden, stellen eine Alternative zum axiomatischen mengentheoretischen Aufbau der Mathematik dar. Darüber hinaus spielt die Kategorientheorie in der Logik, in der Theoretischen Informatik (Semantik von Programmiersprachen, Domaintheorie, Graphgrammatiken) und in der theoretischen Physik (topologische Quantenfeldtheorie, TQFT) eine Rolle.
Inhaltsverzeichnis
Definitionen
Kategorie
Eine Kategorie
 besteht aus den folgenden Daten:
besteht aus den folgenden Daten:- einer Klasse
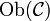 von Objekten
von Objekten - je einer Menge
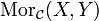 zu jedem Paar (X,Y) von Objekten (auch mit
zu jedem Paar (X,Y) von Objekten (auch mit 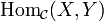 ,
, ![[X, Y]_{\mathcal C}](/pictures/dewiki/100/da340084bbe88584b08392f3bcce166c.png) ,
, 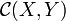 , XY oder (X,Y) bezeichnet); ihre Elemente heißen Pfeile oder Morphismen. Diese Mengen sind paarweise disjunkt, d. h. zu einem Morphismus f in
, XY oder (X,Y) bezeichnet); ihre Elemente heißen Pfeile oder Morphismen. Diese Mengen sind paarweise disjunkt, d. h. zu einem Morphismus f in 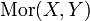 , auch
, auch 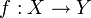 geschrieben, sind X (Quelle) und Y (Ziel) eindeutig bestimmt. Die Quelle eines Morphismus f wird auch mit
geschrieben, sind X (Quelle) und Y (Ziel) eindeutig bestimmt. Die Quelle eines Morphismus f wird auch mit 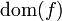 bezeichnet (englisch domain), das Ziel mit
bezeichnet (englisch domain), das Ziel mit 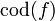 (co-domain).
(co-domain). - Verknüpfungsabbildungen
-
- die im offensichtlichen Sinne assoziativ sind:
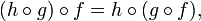 sofern
sofern 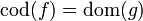 und
und 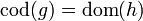 .
.
(Gelegentlich wird das
 weggelassen und
weggelassen und 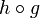 als hg angeschrieben.)
als hg angeschrieben.)- einem Identitätsmorphismus
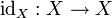 zu jedem Objekt X, der neutrales Element für die Verknüpfung mit Morphismen mit Quelle oder Ziel X ist, d. h. es gilt
zu jedem Objekt X, der neutrales Element für die Verknüpfung mit Morphismen mit Quelle oder Ziel X ist, d. h. es gilt 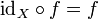 , falls
, falls 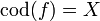 ist, und
ist, und 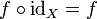 , falls
, falls 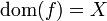 . Anstelle
. Anstelle 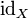 ist auch die Form 1X gebräuchlich.
ist auch die Form 1X gebräuchlich.
Die Klasse aller Morphismen wird auch mit
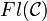 (französisch flèche = Pfeil) bezeichnet.
(französisch flèche = Pfeil) bezeichnet.Unterkategorie
Eine Unterkategorie einer Kategorie
 ist eine Kategorie
ist eine Kategorie 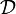 , so dass
, so dass 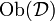 eine Teilklasse von
eine Teilklasse von 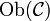 ist und für je zwei Objekte X und Y in D die Morphismenmenge
ist und für je zwei Objekte X und Y in D die Morphismenmenge 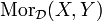 Teilmenge von
Teilmenge von 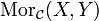 ist. Sind die Morphismenmengen von
ist. Sind die Morphismenmengen von 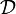 gleich denen von
gleich denen von  , ist
, ist 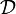 eine volle Unterkategorie. Eine volle Unterkategorie ist schon durch die Angabe der Objekte bestimmt.
eine volle Unterkategorie. Eine volle Unterkategorie ist schon durch die Angabe der Objekte bestimmt.Duale Kategorie
Die duale Kategorie
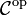 zu einer Kategorie
zu einer Kategorie  ist die Kategorie mit
ist die Kategorie mit 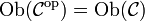 und
und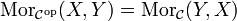 .
.
Die Verknüpfungsabbildungen und Identitätsmorphismen sind dieselben wie in
 . Anschaulich gesagt zeigen in
. Anschaulich gesagt zeigen in 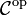 alle Pfeile in die andere Richtung. Die Kategorie
alle Pfeile in die andere Richtung. Die Kategorie 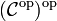 ist gleich
ist gleich  .
.Funktor
Ein (kovarianter) Funktor ist so etwas wie eine strukturerhaltende Abbildung zwischen Kategorien. Ein Funktor F von einer Kategorie
 in eine Kategorie
in eine Kategorie 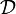 besteht aus den folgenden Daten:
besteht aus den folgenden Daten:- eine Zuordnung
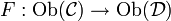
- Abbildungen
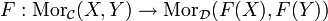 für je zwei Objekte X, Y von
für je zwei Objekte X, Y von  .
.
Die Abbildungen zwischen den Morphismenmengen müssen folgende Eigenschaften haben:
- Sie sind kompatibel mit Verknüpfungen, d. h. F(fg) = F(f)F(g).
- Sie erhalten Identitätsmorphismen:
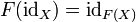 .
.
Ein kontravarianter Funktor (oder Kofunktor) von
 nach
nach 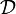 ist ein Funktor
ist ein Funktor 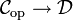 . Äquivalent dazu ist die Beschreibung wie oben, mit den folgenden Unterschieden:
. Äquivalent dazu ist die Beschreibung wie oben, mit den folgenden Unterschieden:- Die Abbildungen auf den Morphismenmengen gehen von
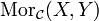 nach
nach 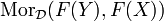 .
. - Die Kompatibilität mit den Verknüpfungen lautet F(fg) = F(g)F(f).
Sind
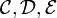 Kategorien und
Kategorien und 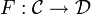 sowie
sowie 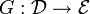 ko- oder kontravariante Funktoren, so ist die Verkettung GF, die formal durch
ko- oder kontravariante Funktoren, so ist die Verkettung GF, die formal durchfür Objekte X und Morphismen f definiert ist, ein Funktor
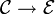 . GF ist genau dann kovariant, wenn F und G beide ko- oder beide kontravariant sind, andernfalls kontravariant.
. GF ist genau dann kovariant, wenn F und G beide ko- oder beide kontravariant sind, andernfalls kontravariant.Natürliche Transformation
Natürliche Transformationen sind so etwas wie Abbildungen zwischen Funktoren. Sind F und G Funktoren von
 nach
nach 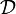 , so besteht eine natürliche Transformation t von F nach G aus Morphismen
, so besteht eine natürliche Transformation t von F nach G aus Morphismen 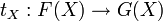 für jedes Objekt X von
für jedes Objekt X von  , so dass für jeden Morphismus f:
, so dass für jeden Morphismus f: 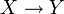 zwischen Objekten von
zwischen Objekten von  das folgende Diagramm kommutiert
das folgende Diagramm kommutiertAls Formel bedeutet das: tYF(f) = G(f)tX.
Natürlich äquivalent sind zwei Funktoren F und G von
 nach
nach 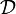 , wenn es natürliche Transformationen
, wenn es natürliche Transformationen 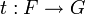 und
und 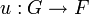 gibt, so dass tu und ut jeweils die Identität sind. Anders formuliert: natürliche Äquivalenz ist der Isomorphiebegriff in der Funktorkategorie. Eine natürliche Transformation t ist eine natürliche Äquivalenz genau dann, wenn tX für jedes X ein Isomorphismus ist.
gibt, so dass tu und ut jeweils die Identität sind. Anders formuliert: natürliche Äquivalenz ist der Isomorphiebegriff in der Funktorkategorie. Eine natürliche Transformation t ist eine natürliche Äquivalenz genau dann, wenn tX für jedes X ein Isomorphismus ist.Äquivalenz von Kategorien: Ein Funktor
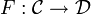 heißt eine Äquivalenz von Kategorien, wenn es einen Funktor
heißt eine Äquivalenz von Kategorien, wenn es einen Funktor 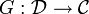 gibt, so dass FG und GF jeweils natürlich äquivalent zur Identität von
gibt, so dass FG und GF jeweils natürlich äquivalent zur Identität von 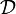 bzw.
bzw.  sind. Man kann zeigen, dass Äquivalenzen von Kategorien genau die volltreuen, wesentlich surjektiven Funktoren sind.
sind. Man kann zeigen, dass Äquivalenzen von Kategorien genau die volltreuen, wesentlich surjektiven Funktoren sind.Beispiele
Kategorien
Hinweis: die Bezeichnungen für spezielle Kategorien sind in der Literatur extrem uneinheitlich. Oft wird eine Beschreibung der Kategorie in runde oder geschweifte Klammern gesetzt, z. B. (Gruppen), oder unterstrichen.
- Die Kategorie Set bzw. Ens (zu engl. set für Menge bzw. franz. ensemble für Menge) ist die Kategorie der Mengen. Die Kategorie besteht aus der Klasse
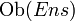 , welche alle Mengen enthält und die Morphismenmenge
, welche alle Mengen enthält und die Morphismenmenge 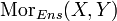 enthält alle Abbildungen von X nach Y. Die Verknüpfung zweier Morphismen ist die Verkettung der Mengenabbildungen.
enthält alle Abbildungen von X nach Y. Die Verknüpfung zweier Morphismen ist die Verkettung der Mengenabbildungen.
- Top bezeichnet die Kategorie der topologischen Räume (Objekte) und stetigen Abbildungen (Morphismen). Eine interessante Unterkategorie ist beispielsweise die volle Unterkategorie der kompakten Hausdorffräume.
- HoTop ist die Homotopiekategorie der topologischen Räume. Die Objekte sind die topologischen Räume und die Morphismen sind die Homotopieklassen.
- die Kategorie Grp der Gruppen mit den Gruppenhomomorphismen als Morphismen; weiter die volle Unterkategorie der abelschen Gruppen, die sehr konsequent mit Ab bezeichnet wird.
- die Kategorie NLinSp der normierten linearen Räume mit den stetigen (=beschränkten) linearen Abbildungen. Unterkategorien sind z. B. die Banachräume mit stetigen linearen Abbildungen (BanSp1), die Banachräume mit stetigen normreduzierenden Abbildungen (BanSp2), oder kommutative komplexe Banachalgebren mit Einheit und normreduzierenden Algebrenhomomorphismen (CBanAlg).
- Eine Menge mit einer Halbordnung
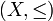 bestimmt eine Kategorie: Objekte sind die Elemente der Menge, und
bestimmt eine Kategorie: Objekte sind die Elemente der Menge, und 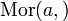 habe genau ein Element (z. B. das geordnete Paar (a,b)), falls
habe genau ein Element (z. B. das geordnete Paar (a,b)), falls 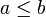 , und sei andernfalls leer.
, und sei andernfalls leer.
- Die Kategorie der kleinen Kategorien (Cat): Eine Kategorie heißt klein, wenn die Klasse ihrer Objekte eine Menge ist. Die Objekte von Cat sind die kleinen Kategorien und die Morphismen sind die Funktoren. (Die Beschränkung auf kleine Kategorien ist aus mengentheoretischen Gründen nötig.)
- Sind
 und
und 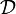 Kategorien, so kann man die Funktorkategorie
Kategorien, so kann man die Funktorkategorie 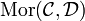 bilden: Objekte sind Funktoren von
bilden: Objekte sind Funktoren von  nach
nach 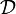 , Morphismen sind natürliche Transformationen.
, Morphismen sind natürliche Transformationen.
- Ist
 eine Kategorie und S ein Objekt von
eine Kategorie und S ein Objekt von  , so ist die Kategorie
, so ist die Kategorie 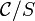 der Objekte über S wie folgt definiert: Objekte von
der Objekte über S wie folgt definiert: Objekte von 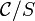 sind Morphismen in
sind Morphismen in  mit Ziel S, und Morphismen von
mit Ziel S, und Morphismen von 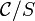 sind Morphismen von
sind Morphismen von  , die mit den „Strukturmorphismen“ nach S verträglich sind, d. h. sind
, die mit den „Strukturmorphismen“ nach S verträglich sind, d. h. sind 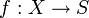 und
und 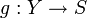 zwei Objekte von
zwei Objekte von 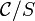 , so sind Morphismen von (X,f) nach (Y,g) in
, so sind Morphismen von (X,f) nach (Y,g) in 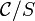 die Morphismen h von X nach Y, für die gh = f gilt.
die Morphismen h von X nach Y, für die gh = f gilt.
- Umgekehrt sei * ein fester einpunktiger topologischer Raum. Dann ist die Kategorie der topologischen Räume unter * isomorph zur Kategorie Top* der punktierten topologischen Räume.
Die meisten der oben genannten Beispiele sind so geartet (oder lassen sich leicht dahingehend anpassen), dass die Objekte Mengen zusammen mit einer Zusatzstruktur sind, die Morphismen Abbildungen, die mit dieser Struktur verträglich sind, und die Verknüpfung von Morphismen die Hintereinanderausführung von Abbildungen ist. Man spricht in diesem Fall von einer konkreten Kategorie. Es ist jedoch nicht jede Kategorie konkret oder auch nur äquivalent zu einer konkreten Kategorie (d. h. konkretisierbar). Nicht konkretisierbar sind beispielsweise (ohne Beweis):
- Die Kategorie hTop mit topologischen Räumen als Objekten und Homotopieklassen stetiger Abbildungen als Morphismen.
- Die Kategorie Rel mit Mengen als Objekten und Relationen als Morphismen, d. h.
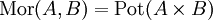 , sowie mit der Verknüpfung
, sowie mit der Verknüpfung 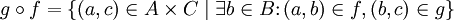 zu
zu 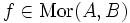 ,
, 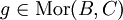 .
.
Funktoren
Meist gibt man für Funktoren nur die Zuordnung der Objekte an, wenn die Abbildungen auf den Morphismenmengen daraus leicht zu ersehen sind.
- Für ein Objekt T einer Kategorie C ist die Zuordnung
-
- X
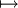 MorC(T,X)
MorC(T,X)
- X
- ein (kovarianter) Funktor C → Set. Der Funktor
- X
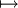 MorC(X,T)
MorC(X,T)
- X
- ist kontravariant. Hierzu siehe auch Hom-Funktor.
- Es sei K ein Körper und VektK die Kategorie der Vektorräume über K mit den K-linearen Abbildungen als Morphismen. Es sei nun ein kontravarianter Funktor
-
- wie folgt definiert:
- Für ein Objekt V ist D(V) = V * = HomK(V,K) der Dualraum von V.
- Für eine lineare Abbildung
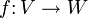 ist
ist
- Man überprüft leicht, dass
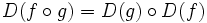 und
und 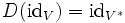 gilt.
gilt.
- Gm: (Ringe) → (Gruppen): ordnet einem unitären Ring seine Gruppe der Einheiten zu. Allgemeiner: GLn: (Ringe) → (Gruppen): ordnet einem Ring die Gruppe der invertierbaren n×n-Matrizen zu.
- Die Fundamentalgruppe ist ein Funktor Top → Grp; die höheren Homotopie- sowie die Homologiegruppen sind Funktoren Top → Ab; die Kohomologiegruppen sind kontravariante Funktoren Top → Ab.
- Vergissfunktoren: Es gibt offensichtliche Funktoren Ab → Set, Ab → Grp, Top → Set usw., die einfach einen Teil der Struktur „vergessen“, d. h. einer abelschen Gruppe die zugrundeliegende Menge, einer abelschen Gruppe sich selbst (aber ohne die Information, dass sie abelsch ist), einem topologischen Raum die zugrundeliegende Menge usw. zuordnen.
- „Freie“ Konstruktionen, hier freie abelsche Gruppe: Jeder Menge S kann man die abelsche Gruppe
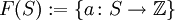 (mit punktweiser Addition) zuordnen. Zusammen mit offensichtlichen Zuordnungen für Abbildungen, nämlich
(mit punktweiser Addition) zuordnen. Zusammen mit offensichtlichen Zuordnungen für Abbildungen, nämlich 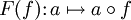 , ergibt sich ein kontravarianter Funktor von Set nach Ab. Es gibt dann eine kanonische Isomorphie
, ergibt sich ein kontravarianter Funktor von Set nach Ab. Es gibt dann eine kanonische Isomorphie 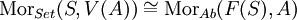 , wobei V der Vergissfunktor ist. Man sagt, F ist (links-)adjungierter Funktor zu V. Ähnliche Konstrukte existieren für viele Vergissfunktoren.
, wobei V der Vergissfunktor ist. Man sagt, F ist (links-)adjungierter Funktor zu V. Ähnliche Konstrukte existieren für viele Vergissfunktoren.
Natürliche Transformationen
- Die Bezeichnungen seien wie im Beispiel des Funktors „Dualraum“ oben. Die Abbildungen
-
- eines Vektorraumes in seinen Bidualraum bilden eine natürliche Transformation
- Auf der vollen Unterkategorie der endlichdimensionalen Vektorräume ist τ eine natürliche Äquivalenz.
- det: GLn → Gm: Für einen Ring R ist detR der Gruppenhomomorphismus GLn(R) → R×, die Determinante.
- Die Hurewicz-Abbildung
- Das Cupprodukt in der Kohomologie.
- Die Abelisierung einer Gruppe
Yoneda-Lemma und universelle Konstruktionen
Universelle Konstruktionen übertragen einfache Begriffe aus der Kategorie der Mengen auf beliebige Kategorien.
Das Yoneda-Lemma
Es sei C eine Kategorie. Der Funktor
der einem Objekt X den Funktor
zuordnet, ist volltreu. Allgemeiner gilt für Objekte X von C und F von Mor(Cop,Set):
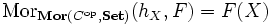 ;
;
einer natürlichen Transformation t: hX → F wird dabei tX(idX) zugeordnet (man beachte hX(X) = MorC(X,X)).
Strukturtransfer
Das Yoneda-Lemma erlaubt es, Begriffe, die aus der Kategorie der Mengen geläufig sind, auf beliebige Kategorien zu übertragen. Beispielsweise kann man ein Produkt von Objekten Xi definieren als ein Objekt P, für das h(P) objektweise das kartesische Produkt der h(Xi) ist, d. h. dass
gilt; dabei meint
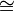 eine natürliche Äquivalenz von Funktoren in T. Diese Äquivalenz liefert für T = P als Entsprechung von idP auch Morphismen pri: P → Xi. Das Yoneda-Lemma zeigt dann, dass P bis auf kanonische Isomorphie eindeutig bestimmt ist: sind Mor(_,P) und Mor(_,Q) via t natürlich äquivalente Funktoren, so sind P und Q via tP(idP) isomorph.
eine natürliche Äquivalenz von Funktoren in T. Diese Äquivalenz liefert für T = P als Entsprechung von idP auch Morphismen pri: P → Xi. Das Yoneda-Lemma zeigt dann, dass P bis auf kanonische Isomorphie eindeutig bestimmt ist: sind Mor(_,P) und Mor(_,Q) via t natürlich äquivalente Funktoren, so sind P und Q via tP(idP) isomorph.„Universell“ ist dieses kategorielle Produkt in dem folgenden Sinn: wann immer man Abbildungen fi: T → Xi gegeben hat, kommen diese von den universellen Abbildungen pri: P → Xi her, d. h. es gibt eine Abbildung c: T → P, so dass fi = pri c gilt.
Außerdem kann man zu jeder derart gewonnenen Konstruktion die duale Konstruktion bilden (meist durch eine Vorsilbe „Ko“ gekennzeichnet), indem man zur dualen Kategorie übergeht. Beispielsweise ist das Koprodukt von Objekten Xi in einer Kategorie C dasselbe wie das Produkt derselben Objekte Xi in der dualen Kategorie Cop.
Entsprechend können auch Eigenschaften von Mengenabbildungen auf beliebige Kategorien übertragen werden: beispielsweise ist ein Morphismus X → Y ein Monomorphismus, wenn h(X) → h(Y) objektweise injektiv ist. Man beachte: Epimorphismus ist der duale Begriff zu Monomorphismus, jedoch die Entsprechung zu surjektiven Mengenabbildungen ist der Begriff Retraktion.
Spezielle universelle Konstruktionen bzw. Begriffe
- Produkt und Koprodukt
- Anfangsobjekte und Endobjekte
- Differenzkern und Differenzkokern
- Faserprodukt und push-out
- allgemein Limites bzw. Kolimites
- injektive und projektive Objekte
- Adjungierte Funktoren
Anmerkungen
Zu einem anderen allgemeinen Zugang zu mathematischen Strukturen siehe Algebraische Struktur.
Mathematical Subject Classification (2000): 18-XX (mit homologischer Algebra in 18Gxx)
Siehe auch: Homologische Algebra sowie Kategorie (Allgemeinbegriff) und Kategorie in der Philosophie
Literatur
Einführungen sind:
- F. W. Lawvere, S. H. Schanuel: Conceptual Mathematics. A first introduction to categories, Cambridge, 1997. ISBN 0-521-47817-0 (hardback ISBN 0-521-47249-0).
- Steve Awodey: Category Theory, Claredon Press, Oxford, 2006. ISBN 978-0-19-856861-2.
- Michael A. Arbib, Ernest G. Manes: Arrows, Structures and Functors. The Categorical Imperative, Academic Press, 1975.
- Hartmut Ehrig, Michael Pfender und Studenten der Mathematik und Informatik: Kategorien und Automaten, Walter de Gruyter, Berlin, New York, 1972. ISBN 3-11-003902-8 (Das Buch gibt in den Kapiteln 1, 3 und 5 eine in sich abgeschlossene Einführung in die allgemeine Kategorientheorie und in den Kapiteln 2, 4 und 6 wird die Automatentheorie mit kategoriellen Methoden entwickelt.)
Klassische Lehrbücher sind:
- J. Adámek, H. Herrlich, G.E. Strecker: Abstract and concrete categories, John Wiley (1990)
- MacLane, Saunders: Kategorien: Begriffssprache und mathematische Theorie, Berlin, 1972, vii, 295 pp. – (Categories for the Working Mathematician <1971, deutsch>) vergriffen engl. Ausgabe ISBN 0-387-98403-8
- Mac Lane, Saunders: Categories for the Working Mathematician, 2nd edition, Springer, 1998, ISBN 0-387-98403-8
- Herrlich, Horst; Strecker, George E.: Category Theory. An Introduction, Boston, 1973
- Schubert, Horst: Kategorien I/II, Springer, 1970.
Ein Nachschlagewerk ist:
- Borceux, Francis: Handbook of categorical algebra, 3 vol (1: Basic category theory; 2: Categories and structures; 3: Categories of sheaves). – Cambridge, 1994. (Encyclopedia of Mathematics and its Applications, 50/52) ISBN 0-521-44178-1, 0-521-44179-X, 0-521-44180-3
Ein Sammelband ist:
- W Gähler & G Preuss: Categorical Structures and their Applications, World Scientific, 2004. ISBN 981-256-053-X
Siehe auch
Weblinks
- Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
- Category theory, homological algebra im Mathematical Atlas
- PlanetMath Übersichtsartikel (engl.)
- eine „freundliche Einführung“ in die Kategorientheorie, die nur mit Beispielen aus der Algorithmik arbeitet (engl.) Postscript, 80 S.
- categories, moderierte Liste von Kategorientheoretikern über Kategorientheorie
- einer Klasse
Wikimedia Foundation.

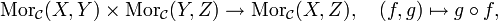
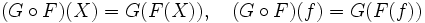
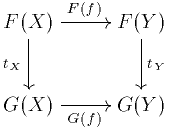
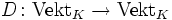
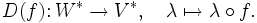
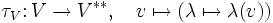
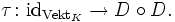
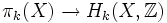
![G\to G^{\mathrm ab}:=G/[G,G]](/pictures/dewiki/49/1302b6782c3052e7f6641dc409da1be1.png)