Rektaszension

Rektaszension und Deklination

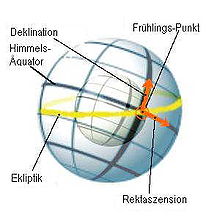
Die Rektaszension (aus dem Lateinischen für „gerader Aufstieg“; gebräuchlichste Abkürzungen: α und RA, vom englischen right ascension; auch RA, von lat. ascensio recta), auch Himmlischer Längengrad genannt, ist in der Astronomie der Winkel zwischen dem Längenkreis des Frühlingspunktes bis zum Längenkreis, über dem das beobachtete Objekt steht, auf der Äquatorebene gemessen. Er ist die Entsprechung auf der (imaginären) Himmelskugel zur geographischen Länge auf der Erde.

Äquatoriales Koordinatensystem

Himmelsäquator und Ekliptik

Die Rektaszension ist die eine Koordinate des mit der Himmelskugel mitrotierenden äquatorialen Koordinatensystems, die andere heißt Deklination (δ).

Als Nullpunkt der Rektaszension dient dabei der Frühlingspunkt. Die Rektaszension wird wie die geografische Länge gegen den Uhrzeigersinn, also nach Osten gemessen.

In der Astronomie hat sich durchgesetzt, die Rektaszension nicht in Grad, sondern im Zeitmaß in Stunden anzugeben, wobei der Vollkreis von 360° in 24 „Stunden“ eingeteilt wird.

In der astronomischen Navigation wird statt der Rektaszension auch der Sternwinkel (engl. sidereal hour angle (SHA)) verwendet, der vom Frühlingspunkt aus nach Westen gezählt wird.

Im ortsfesten äquatorialen Koordinatensystem wird statt der Rektaszension der Stundenwinkel verwendet.

Rektaszension α und Deklination δ lassen sich mittels der Ekliptikschiefe ε in die ekliptikale Länge λ und die ekliptikale Breite β des ekliptikalen Koordinatensystems umrechnen – siehe kleines Dreieck rechts auf der Skizze. Diese Koordinatentransformation ist für die Berechnung der Umlaufbahnen von Planeten und anderer Körper des Sonnensystems unerlässlich.

Abschätzung der Sichtbarkeit

Bei bekannter Rektaszension eines Sternes oder anderer astronomischer Objekte ist leicht abzuschätzen, zu welcher Zeit im Jahr das Objekt am besten zu beobachten ist, indem das Datum berechnet/abgeschätzt wird, an dem seine höchste Erhebung über dem Horizont in etwa auf Mitternacht fällt (Opposition). Der Trifidnebel z. B. hat eine Rektaszension von rund 18^h. Wenn man das Verhältnis von 18 Stunden zu den 24 Stunden des Vollkreises berechnet und auf die zwölf Monate des vollen Jahres bezieht, erhält man neun Monate. Zum Frühlingspunkt (21. März) addiert ergibt sich so ein Datum um den 21. Dezember. Das ist der Zeitpunkt, an dem die höchste Erhebung am Horizont auf 12 Uhr Mittag fällt. Daher liegt die optimale Sichtbarkeit sechs Monate davor oder danach, also etwa am 21. Juni. Diese Rechnung ist unabhängig vom Beobachtungsort, es ist aber trotzdem möglich, dass das Objekt unter dem Horizont steht. Der Trifidnebel hat eine Deklination von etwa −22 Grad und ist daher in unseren Breiten nur schwer zu beobachten (Höchststand nur rund 20 Grad in Süddeutschland); in Norwegen ist er das ganze Jahr nicht zu sehen.

Weblinks

• Rektaszension – der himmlische Längengrad – Seite bei BR-online