Stundenwinkel

Stundenwinkel und Deklination im ortsfesten äquatorialen Koordinatensystem

Der Stundenwinkel und die Deklination sind die Koordinaten eines Gestirns im ortsfesten äquatorialen Koordinatensystem, mit denen seine Position bezüglich eines Beobachtungsortes auf der Erde beschrieben werden kann. Man spricht vom Stundenwinkel, weil er sich unter anderem für die Zeitmessung eignet und daher üblicherweise im Zeitmaß angegeben wird. Er entspricht jener Zeit, die seit der letzten Kulmination des Gestirns vergangen ist.

Definition

Ein Himmelskörper mit dem Stundenwinkel 56° aus der Sicht eines Beobachters auf der geographischen Breite 42°N

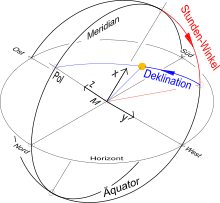
Der Stundenwinkel ist der Winkel, unter dem sich die vom Großkreis (Stundenkreis) durch den Himmelskörper und die Himmelspole und dem Meridian aufgespannten Ebenen schneiden.

Er wird in der Ebene des Himmelsäquators vom Meridian aus in Richtung der scheinbaren täglichen Bewegung der Himmelskugel gemessen, also positiv in westlicher Richtung (für einen nach Süden blickenden Beobachter „nach rechts“) und negativ in östlicher Richtung („nach links“). Tritt ein Gestirn durch den Meridian, hat es in diesem Augenblick den Stundenwinkel Null.

Stundenwinkel einiger Himmelskörper

Der Stundenwinkel jener Himmelskörper, welche der westwärts gerichteten scheinbaren täglichen Bewegung des Himmels folgen, wächst stets in positiver Richtung an. Anders verhält es sich beispielsweise bei denjenigen Erdsatelliten, welche die Erde von West nach Ost umkreisen und deren Stundenwinkel daher in negativer Richtung wächst, oder bei geostationären Satelliten, deren Stundenwinkel konstant bleibt.

Der Stundenwinkel der meisten Himmelskörper ändert sich rasch. Der Stundenwinkel eines Sterns wächst während eines siderischen Tages von ca. 23^h 56^m um 360°, in einer Stunde also um 15,04°. Man beachte, dass der Stundenwinkel zu unterscheiden ist vom Bogen, den der Himmelskörper auf der Himmelskugel zurücklegt: dieser beträgt zum Beispiel für einen Stern auf dem Himmelsäquator ebenfalls 15,04° pro Stunde, für einen Stern mit der Deklination 50° aber nur 15,04°·cos(50°) = 0.6428·15,04° = 9,6675° pro Stunde.

Da die Sonne sich bezüglich der Sterne um etwa ein Grad pro Tag in östlicher Richtung bewegt, wächst ihr Stundenwinkel etwas langsamer an als der eines Sterns. Er wächst auch mit etwas ungleichmäßiger Geschwindigkeit, was mit Hilfe der Zeitgleichung erfasst wird. Man kann eine so genannte mittlere Sonne derart definieren, dass diese Geschwindigkeitsschwankungen ausgeglichen sind. Deren Stundenwinkel wächst mit konstanter Geschwindigkeit 15° pro Stunde. Die mit der Zeitgleichung korrigierte scheinbare Bewegung der Sonne ist als sogenannte mittlere Sonnenzeit die Grundlage unserer heutigen Zeitmessung. Bis zur Mitte des 19. Jahrhunderts begnügte man sich mit der leicht schwankenden sogenannten wahren Sonnenzeit. Die Sonnenzeit ist der um 12 Stunden vermehrte Stundenwinkel der Sonne. Der glatte Zahlenwert „15° pro Stunde“ folgt aus der ursprünglichen Definition der Stunde. Sie war definiert als 1/24 eines Sonnentages, des Zeitraums zwischen zwei Meridiandurchgängen der Sonne, in welchem ihr Stundenwinkel um 360° wächst. Während 1/24 dieses Zeitraums wächst der Stundenwinkel um 360°/24 = 15°.

Auch der Stundenwinkel eines Sterns kann zur Zeitmessung verwendet werden. Er ist gleich der seit dem letzten Meridiandurchgang des Sterns verstrichenen Sternzeit.

Aufgrund dieser Eignung zur Zeitmessung wird der Stundenwinkel statt im Gradmaß oft auch im Zeitmaß (in Stunden, Minuten und Sekunden) angegeben (15° = 1 Stunde). Er gibt dann unmittelbar die seit dem Meridiandurchgang der Sonne bzw. des Sterns verstrichene Sonnen- bzw. Sternzeit an. Die dabei verwendeten Zeitminuten und Zeitsekunden dürfen nicht verwechselt werden mit den Bogenminuten und den Bogensekunden eines im Gradmaß gegebenen Winkels.

Stundenwinkel und parallaktische Montierung

Parallaktische Montierungen von astronomischen Beobachtungsinstrumenten ermöglichen die getrennte Messung der ortsfesten äquatorialen Koordinaten Stundenwinkel und Deklination. Sie enthalten je eine Drehachse, um der Änderung der beiden Koordinaten zu folgen. Ändert sich der Stundenwinkel gleichmäßig wie bei Sternen, so lässt sich das Instrument automatisch mit Hilfe eines Antriebs an der zur Himmelsachse parallelen Deklinationsachse (oder Stundenachse) nachführen. Weil sich die Deklination der Sterne nicht ändert, kann bei deren Beobachtung die Deklinationsachse arretiert werden.

Stundenwinkel und Rektaszension

Stundenwinkel und Rektaszension sind die einander entsprechenden Koordinaten im ortsfesten beziehungsweise im rotierenden äquatorialen Koordinatensystem. Bezugsebene des Rektaszensions-Winkels ist nicht die ortsfeste Meridianebene, sondern die rotierende Ebene, die vom Großkreis durch den Frühlingspunkt und die Himmelspole aufgespannt wird. Die Rektaszension wird positiv in östlicher Richtung - also entgegengesetzt zum Stundenwinkel - gezählt. Die Deklination ist in beiden Systemen identisch, denn sie bezieht sich beide male auf die Äquatorebene.

Stundenwinkel τ und Rektaszension α sind über die Sternzeit θ miteinander verknüpft:

τ = θ − α .

Der Stundenwinkel des Frühlingspunkts ist identisch mit der Sternzeit am Standort. Er ist null, wenn der fiktive Frühlingspunkt den (örtlichen) Meridian passiert. In diesem Moment sind Stundenwinkel und Rektaszension für alle Himmelskörper gleich groß, unterschiedlich sind nur die Vorzeichen.

Die Umrechnung zwischen Stundenwinkel und Rektaszension ist unter anderem im Hauptartikel Astronomische Koordinatensysteme beschrieben.

Siehe auch

• Astronomische Koordinatensysteme zur genaueren Erläuterung der verschiedenen Himmelskoordinaten
• Nautisches Dreieck zur Umrechnung zwischen verschiedenen Koordinatensystemen
• Ortsstundenwinkel