- Reversionspendel
-
Das Wort Reversionspendel bezeichnet in der Gravimetrie ein Pendel zur präzisen Messung der Schwerebeschleunigung. Es hat zwei verstellbare Punkte oder Achat-Schneiden zur Aufhängung und Justierung der verstellbaren Pendelmassen.
Die Besonderheit von Reversionspendeln besteht darin, dass die zwei Aufhängepunkte so eingestellt werden, dass sie exakt dieselbe Schwingungsperiode besitzen. Damit wird das schwierige Problem umgangen, den Schwerpunkt des Pendels zu bestimmen, um die Pendellänge genau zu bestimmen.
Diese Aufgabe reduziert sich auf die Messung der Distanz zwischen den beiden Schneiden, deren Wert die in die Schwingungsformel einzugebende Pendellänge ist.
Mit diesem Verfahren hat man bereits vor der Jahrhundertwende die Erdschwerebeschleunigung g auf etwa ein Millionstel ihres Wertes bestimmen können (siehe Pendelapparat von Sterneck). Die um die Mitte des 20. Jahrhunderts entwickelten Gravimeter nach dem Prinzip der Federwaage haben diese Genauigkeit nur durch hohen Aufwand an Konstruktion, Rechenmethoden und Reduktionen erreicht, sind aber mittlerweile um den Faktor 10 bis 100 genauer geworden.
Nach Angabe mehrerer Quellen wurde das Reversionspendel von Johann Gottlieb Friedrich von Bohnenberger erfunden.
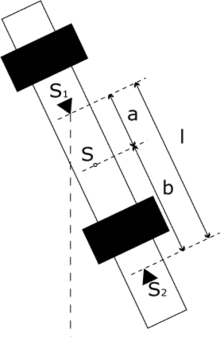
Funktionsprinzip
Die Abbildung zeigt den schematischen Aufbau eines Reversionspendels mit zwei verschiebbaren Massen.
Wenn JS das Trägheitsmoment bezüglich des Schwerpunkts S des Pendels ist, gilt nach dem Steinerschen Satz für das Trägheitsmoment J bezüglich der Schneide S1 im Abstand a vom Schwerpunkt
 .
.
Daraus ergibt sich für kleine Auslenkungen die Schwingungsdauer
 .
.
Analoges gilt für S2.
Bestimmt man nun die Positionen der Massen so, dass die Schwingungsdauern
 und
und  für Schwingungen um S1 bzw. S2 gleich sind, erhält man mit a + b = l (l: Reduzierte Pendellänge):
für Schwingungen um S1 bzw. S2 gleich sind, erhält man mit a + b = l (l: Reduzierte Pendellänge): .
.
Analoge Überlegungen gelten für Reversionspendel mit verstellbaren Schneiden. Kann man den Abstand zwischen den Schneiden sehr genau messen, lässt sich – eine exakte Schwingungsdauermessung vorausgesetzt – mit diesem Experiment die Erdbeschleunigung g sehr präzise bestimmen.
Weblinks & Literatur
- 1997 Uni Bonn (PDF-Datei; 13 kB)
- Uni Tübingen
- Physikpraktikum RP TU Dresden (PDF-Datei; 670 kB)
- Friedrich Georg Wieck, Otto Wilhelm Alund: Naturkrafterna och deras användning (Naturkräfte und deren Anwendung) (1873-1875), S. 99 [1]
Kategorien:- Dimensionales Messgerät
- Geophysik
- Geodätisches Instrument
- Schwingung
Wikimedia Foundation.