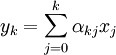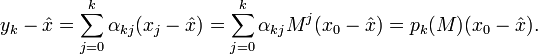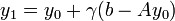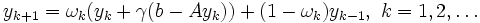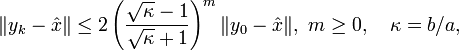Tschebyscheff-Iteration

Die Tschebyschow-Iteration (nach Pafnuti Lwowitsch Tschebyschow) ist ein numerisches Verfahren zur Lösung von linearen Gleichungssystemen Ax = b mit 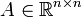$A \in \R^{n \times n}$ und wird auch als semi-iteratives Verfahren bezeichnet, da sie als ein einfacher Iterationsschritt eines Splitting-Verfahrens mit nachgeschalteter Extrapolation interpretiert werden kann. Grundlage ist die Rekursionsformel für Tschebyschow-Polynome. Das Verfahren erreicht für symmetrisch-definite Matrizen die Geschwindigkeit des CG-Verfahrens, kann aber auch für unsymmetrische Matrizen angepasst werden, wenn Informationen über die Lage der Eigenwerte vorliegen.

Das semi-iterative Verfahren

Grundlage ist die Idee, dass man aus der Vektorfolge 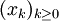$(x_k)_{k\ge0}$, die man mit einem Splitting-Verfahren erhält, durch allgemeine Linearkombination eine bessere Folge

$y_k = \sum_{j=0}^k\alpha_{kj}x_j$

konstruiert. Um eine exakte Lösung 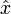$\hat x$ nicht wieder zu verlassen, ist 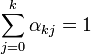$\sum_{j=0}^k\alpha_{kj}=1$ erforderlich. Da für die Fehler beim Splitting-Verfahren 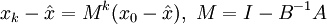$x_k-\hat x=M^k(x_0-\hat x),\ M=I-B^{-1}A$ gilt, erhält man für den neuen Fehler

$y_k-\hat x=\sum_{j=0}^k\alpha_{kj}(x_j-\hat x)=\sum_{j=0}^k\alpha_{kj}M^j(x_0-\hat x)=p_k(M)(x_0-\hat x).$

Also wird der Startfehler 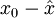$x_0-\hat x$ mit dem Matrix-Polynom p_k(M) multipliziert mit dem Ziel, diesen zu verkleinern. Hat die Matrix A nur reelle Eigenwerte in einem Intervall $[a,b],\,a>0,$, ist dasjenige Polynom mit kleinster Schranke für den Spektralradius ρ(p_k(A)) ein verschobenes Tschebyschow-Polynom T_k. Da für letztere eine zweistufige Rekursionsformel gilt, kann die Tschebyschow-Iteration ebenfalls als zweistufiges Verfahren ausgeführt werden:

$\,\! y_1= y_0+\gamma (b-Ay_0)$

$y_{k+1} = \omega_k(y_k+\gamma (b-Ay_k))+(1-\omega_k)y_{k-1},\ k=1,2,\ldots$

mit den Parametern

$\gamma=\frac{2}{a+b},\quad \omega_k=2\mu\frac{T_k(\mu)}{T_{k+1}(\mu)},\quad \mu=\frac{b+a}{b-a}.$

In der Vorschrift für y_{k + 1} ist zu erkennen, dass in der Klammer ein optimaler Schritt des Richardson-Verfahrens steht.

Für eine symmetrisch-definite Matrix A ist diese Iteration eng verwandt mit dem CG-Verfahren, welches aber die Parameter γ,ω_k anders bestimmt, und besitzt die gleiche Konvergenzgeschwindigkeit. Die Tschebyschow-Iteration kann aber auch auf unsymmetrische Matrizen mit komplexen Eigenwerten angewendet werden, wenn diese sich in einer Ellipse einschließen lassen, welche den Nullpunkt nicht enthält.

Konvergenz des Verfahrens

Für eine symmetrische, positiv definite Matrix A gilt in der euklidischen Norm die Fehlerschranke

$\|y_k-\hat x\|\le 2\left(\frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1}\right)^m\|y_0-\hat x\|, \ m\ge0,\quad \kappa=b/a,$

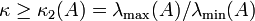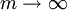ähnlich dem CG-Verfahren, wobei κ eine Schranke für die Konditionszahl der Matrix A ist $\kappa\ge \kappa_2(A)=\lambda_{\rm max}(A)/\lambda_{\rm min}(A)$. Für $m\to\infty$ geht der Fehler offenbar gegen null.

Der Konvergenzvorteil gegenüber dem einfachen Splitting-Verfahren bzw. Richardson-Verfahren ist, dass die Konvergenz nur von der Wurzel der Kondition abhängt. Bei komplexen Eigenwerten geht dieser Vorteil umso mehr verloren, je runder die zur Einschließung benötigte Ellipse wird. Bei Einschließung mit einem Kreis schließlich ist das einfache Verfahren mit 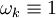$\omega_k\equiv1$ optimal.

Literatur

• Gene H. Golub, Charles van Loan: Matrix Computations, Johns Hopkins University Press.