- Rutherford-Streuung
-
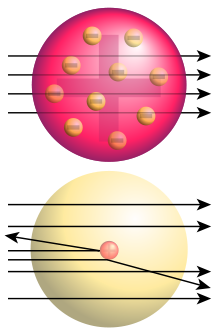
Die Rutherford-Streuung beschreibt die Streuung von geladenen Partikeln an einem geladenen Streuzentrum. Im Ausgangsversuch wurde die Streuung von Alpha-Teilchen an Gold-Atomkernen untersucht. Die sich daraus ergebenden Teilchenbahnen sind Hyperbeln. Die Verteilung der gestreuten Teilchen lässt auf die Struktur des Streuzentrums rückschließen. Dies führte zur Erkenntnis, dass die positive Ladung in den Atomen sich auf einen kleinen Raum im Atomzentrum konzentriert. Bis dahin galt das Modell von J.J. Thomson, bei dem die positive Ladung des Atoms homogen in einer Kugel verteilt ist (thomsonsches Atommodell). Beteiligt an diesen Experimenten waren Hans Geiger, Ernest Marsden und Ernest Rutherford. Bei der Betrachtung der Messergebnisse, die darauf hinweisen, dass die Masse des Atoms in einem kleinen Kern konzentriert ist, soll Rutherford gesagt haben: „Dies ist so unwahrscheinlich, als ob man mit einer Pistole auf einen Wattebausch schießt, und die Kugel zurückprallt.“
Inhaltsverzeichnis
Rutherfordscher Streuversuch (Manchester, 1909-1913)
Aufbau und Versuchsdurchführung
In einen Bleiblock mit Öffnung zu einer Seite hin wird ein radioaktiver Stoff gelegt, der Strahlung abgibt: Alpha-, Beta- und Gamma-Strahlung. Diese Strahlen werden durch die Öffnung im Bleiblock durch ein elektrisches Feld geleitet. Die Beta-Strahlen lenkt man zum positiven Pol hin ab, die Alpha-Strahlen zum negativen Pol und die Gamma-Strahlen bleiben unverändert. Die Alpha-Strahlung wird durch eine (ca. 1000 Atome) dünne Goldfolie geleitet. Die Strahlung lässt sich danach mit einem Leuchtschirm sichtbar machen. Es wurde Gold verwendet, da es sich schon damals mit einfachen mechanischen Mitteln zu sehr dünnen Schichten verarbeiten ließ und eine hohe Atommasse besitzt.
Beobachtung
- Der Großteil der Alpha-Teilchen kann die Goldfolie (mehr oder weniger) ungehindert passieren.
- Größere Streuwinkel kommen immer seltener vor, je größer der Winkel ist.
- Auch Streuwinkel von über 90° gibt es, aber extrem selten.
- Einige Alpha-Teilchen werden zurück gestreut.
- Die Verteilung entspricht der Rutherfordschen Streuformel.
Interpretation
Die Ablenkung der Alpha-Teilchen und ihre Winkelverteilung lassen sich dadurch verstehen, dass sich in den Atomen ein sehr kleines Massezentrum befindet, das positiv geladen ist. Man nennt dieses Massezentrum den Atomkern. Die meisten Teilchen passieren die Goldfolie ungehindert, d.h. dass zwischen den Kernen ein großer Freiraum besteht. Das Ergebnis führte auf das rutherfordsche Atommodell. Die Elektronen, welche um den Kern kreisen, schirmen die positive Kern-Ladung ab, sodass das Atom nach außen hin neutral erscheint.
Rutherfordsche Streuformel
Die rutherfordsche Streuformel gibt den so genannten differenziellen Streuquerschnitt (auch Wirkungsquerschnitt genannt) im Schwerpunktsystem an:
Die gleiche Formel in kernphysikalisch sinnvollen Einheiten:
Damit ist die Wahrscheinlichkeit beschrieben, dass gestreute Teilchen nach einer Ablenkung um den Winkel
 im Raumwinkel
im Raumwinkel  auftreffen.
auftreffen.In der Formel werden weiterhin folgende Größen benutzt:
Elektrische Feldkonstante (Dielektrizitätskonstante) 
Ladung des gestreuten Teilchens Z1e Ladung des Atomkerns Z2e Elementarladung 
Anfangsenergie des gestreuten Teilchens E0 Auf den Vorfaktor kommt man, indem man folgende Größen verwendet:
Feinstrukturkonstante 
Einheit für den Wirkungsquerschnitt 1barn = 100fm2 
Rutherford leitete die rutherfordsche Streuformel aus der klassischen Physik her. Eine vollständige quantenmechanische Behandlung des Problems mit Hilfe der bornschen Näherung ergibt, dass die rutherfordsche Streuformel in erster Ordnung korrekt ist und quantenmechanische Effekte nur kleine Korrekturen darstellen. Ein weiteres Problem der rutherfordschen Formel ist der Grenzfall
 , für die der differentielle Wirkungsquerschnitt unendlich groß wird. Kleine Winkel entsprechen jedoch einem großen Stoßparameter. Bei sehr großen Stoßparametern schirmen die Atomelektronen den Kern jedoch ab. Die einzige Möglichkeit sehr kleine Winkel bei kleinen Stoßparametern zu haben, ist die Energie der α-Teilchen zu erhöhen. Für sehr hohe Energien kann die Ladungsverteilung des Atomkerns jedoch nicht mehr als punktförmig angenommen werden. Dann geht der Formfaktor der Ladungsverteilung zusätzlich in die Streuformel ein. Außerdem kann man bei hohen Projektilenergien nicht mehr davon ausgehen, dass die Streuung nur durch elektromagnetische Wechselwirkung geschieht. Nähern sich beide Kerne bis zu einem Kontaktradius, spielt die starke Wechselwirkung eine größere Rolle.
, für die der differentielle Wirkungsquerschnitt unendlich groß wird. Kleine Winkel entsprechen jedoch einem großen Stoßparameter. Bei sehr großen Stoßparametern schirmen die Atomelektronen den Kern jedoch ab. Die einzige Möglichkeit sehr kleine Winkel bei kleinen Stoßparametern zu haben, ist die Energie der α-Teilchen zu erhöhen. Für sehr hohe Energien kann die Ladungsverteilung des Atomkerns jedoch nicht mehr als punktförmig angenommen werden. Dann geht der Formfaktor der Ladungsverteilung zusätzlich in die Streuformel ein. Außerdem kann man bei hohen Projektilenergien nicht mehr davon ausgehen, dass die Streuung nur durch elektromagnetische Wechselwirkung geschieht. Nähern sich beide Kerne bis zu einem Kontaktradius, spielt die starke Wechselwirkung eine größere Rolle.Plausibilitätsbetrachtung der Abhängigkeiten
Nach den Feynman-Regeln ergibt sich für die Streuung eines Teilchens der Ladung Z1e an einem zweiten Teilchen der Ladung Z2e für die Wahrscheinlichkeitsamplitude
wobei der Propagator vernachlässigt wurde. Nach Fermis Goldener Regel gilt
womit folgt, dass
Herleitung der Rutherford-Streuformel
Aufgrund der abstoßenden Wirkung der Coulombkraft

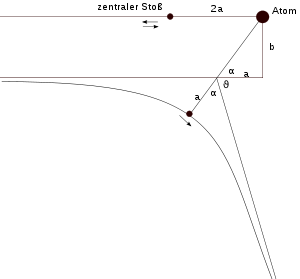
ergibt sich für die Bahn des Alphateilchens (Z1 = 2) eine Hyperbel.Die große Halbachse a der Hyperbel lässt sich aus dem Ansatz
bestimmen, wobei 2a der minimale Abstand des Alphateilchens ist, wenn es zentral mit dem Kern stößt. a ist von der kinetischen Energie abhängig und kann auch für Stöße, die nicht zentral sind, übernommen werden. Der Stoßparameter b ist der minimale Abstand des Alphateilchens zum Kern, wenn es auf einer Geraden weiter fliegen würde. Tatsächlich wird das Alphateilchen um den Winkel
 gestreut. Aus der Geometrie der Hyperbel erhält man folgende Gleichungen:
gestreut. Aus der Geometrie der Hyperbel erhält man folgende Gleichungen:und damit
 .
.
Durch Ableitung der letzten Formel erhält man einen Zusammenhang zwischen der Breite db eines Hohlkegels und der zugehörigen Breite
 des Ablenkwinkels
des Ablenkwinkels .
.Sei
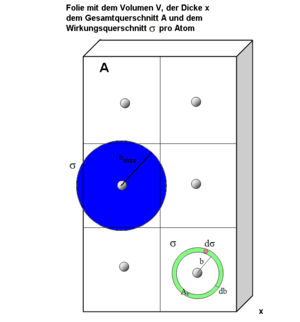
 die Teilchendichte (n Atome pro Volumen V) des Streumaterials und x die Dicke der Folie, so gibt
die Teilchendichte (n Atome pro Volumen V) des Streumaterials und x die Dicke der Folie, so gibt  die durchschnittliche Querschnittsfläche pro Atom an, die das Alphateilchen beim Durchgang durch die Folie erfährt. σ nennt man auch den Wirkungsquerschnitt.
die durchschnittliche Querschnittsfläche pro Atom an, die das Alphateilchen beim Durchgang durch die Folie erfährt. σ nennt man auch den Wirkungsquerschnitt.Die Wahrscheinlichkeit
 im Ring des Hohlzylinders zu landen ergibt sich dann aus
im Ring des Hohlzylinders zu landen ergibt sich dann aus .
.
Von N Teilchen werden dN' in den Hohlkegel gestreut. Die Wahrscheinlichkeit dafür istdN gibt die Anzahl der Teilchen in den Raumwinkel dΩ an.
Daraus folgt : .
.
So ergibt sich für die Wahrscheinlichkeit
Dies ist die Rutherford-Streuformel. Sie gibt an, wie hoch die Wahrscheinlichkeit für ein Teilchen ist, in den Raumwinkel dΩ gestreut zu werden.Oft wird die Streuformel mit Hilfe des differentiellen Wirkungsquerschnitts
 angegeben. Er ist ein Maß für die gleiche Wahrscheinlichkeit.
angegeben. Er ist ein Maß für die gleiche Wahrscheinlichkeit.Es gilt
und damit
.
Bemerkungen
1)
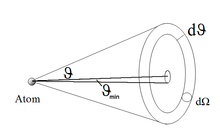
 ist nicht definiert, da es einen minimalen Ablenkwinkel
ist nicht definiert, da es einen minimalen Ablenkwinkel  gibt. Dieser wird angenommen, wenn sich das Alphateilchen im Abstand b = bmax vom Atom, also am Rand der kreisförmigen Wirkungsquerschnittsfläche bewegt. Für einen größeren Stoßparameter b befindet sich das Alphateilchen im Streufeld des Nachbaratoms und der Ablenkwinkel nimmt wieder zu. Dabei gilt:
gibt. Dieser wird angenommen, wenn sich das Alphateilchen im Abstand b = bmax vom Atom, also am Rand der kreisförmigen Wirkungsquerschnittsfläche bewegt. Für einen größeren Stoßparameter b befindet sich das Alphateilchen im Streufeld des Nachbaratoms und der Ablenkwinkel nimmt wieder zu. Dabei gilt:- und
-
 .
.
2) Das Integral über die Wahrscheinlichkeitsverteilung
 ergibt 1
ergibt 13) Ähnliches gilt für die Flächenintegrale
- und
Literatur
- E. Rutherford, The Scattering of α and β Particles by Matter and the Structure of the Atom, Philosophical Magazine. Series 6, 21 (May 1911) p. 669-688
- H. Geiger and E. Marsden, On a Diffuse Reflection of the α-Particles, Proceedings of the Royal Society 82A (1909), p. 495-500
- H. Geiger and E. Marsden, LXI. The Laws of Deflexion of a Particles through Large Angles, Philosophical Magazine 25 (1913), p. 604-623
- Gerthsen, Kneser, Vogel: Physik, 16. Auflage, S.630 - 633, Springer-Verlag
Weblinks
- LP - Rutherfordsches Streuexperiment (inkl. Skizzen, Fotos, Video und Literaturhinweisen)
- Rutherfordstreuung - Moderne Physik mit Maple
- Animation bei chimie.de
Wikimedia Foundation.


![\frac{\mathrm{d}\sigma} {\mathrm{d}\Omega} [\mathrm{barn}] \approx 1{,}3 \cdot 10^{-3} \left(\frac{Z_1 Z_2}{E_0[\mathrm{MeV}]}
\right)^2\frac{1}{ \sin^4 \left( \frac{\vartheta}{2} \right) }](a/1ea0ba1164dee14b1a1d5034748701b5.png)