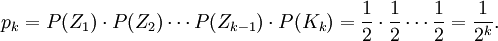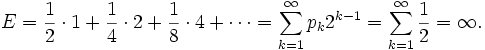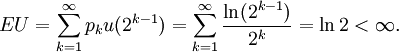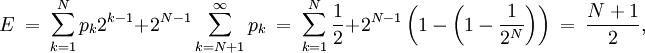Sankt-Petersburg-Lotterie

Das Sankt-Petersburg-Paradoxon (oft auch Sankt-Petersburg-Lotterie) beschreibt ein Paradoxon in einem Glücksspiel. Die Zufallsvariable hat hier einen unendlichen Erwartungswert, was gleichbedeutend mit einer unendlich großen erwarteten Auszahlung ist. Trotzdem scheint der Spieleinstieg nur einen kleinen Geldbetrag wert zu sein. Das St.-Petersburg-Paradoxon ist eine klassische Situation, in der eine naive Entscheidungstheorie, die nur den Erwartungswert als Kriterium verwendet, eine Entscheidung empfehlen würde, die keine (reale) rationale Person fällen würde. Das Paradoxon kann gelöst werden, indem das Entscheidungsmodell durch die Verwendung einer Nutzenfunktion verfeinert wird, oder indem endliche Varianten der Lotterie betrachtet werden.

Das Paradox erhielt seinen Namen von Daniel Bernoullis Präsentation des Problems und seiner Lösung, die er 1738 in den Commentarii Academiae Scientiarum Imperialis Petropolitanae veröffentlichte. Nikolaus I. Bernoulli erwähnte das Problem jedoch schon 1713 in einem Briefwechsel mit Pierre Rémond de Montmort.

Das Paradoxon

In einem Glücksspiel, für das eine Teilnahmegebühr verlangt wird, wird eine faire Münze geworfen, solange bis zum ersten Mal "Kopf" fällt. Dies beendet das Spiel. Der Gewinn richtet sich nach der Anzahl der Münzwürfe insgesamt. War es nur einer, dann erhält der Spieler 1 Euro. Bei zwei Würfen (also einmal "Zahl", einem "Kopf") erhält er 2 Euro, bei drei Würfen 4 Euro, bei vier Würfen 8 Euro und bei jedem weiteren Wurf verdoppelt sich der Betrag. Man gewinnt also 2^k−1 Euro, wenn die Münze k mal geworfen wurde. (In der ursprünglichen Darstellung spielt sich diese Geschichte in einem hypothetischen Kasino in Sankt Petersburg ab, daher der Name des Paradoxons)

Welchen Geldbetrag würde man für die Teilnahme an diesem Spiel bezahlen wollen?

Sei P(Z_i) die Wahrscheinlichkeit, dass beim i-ten Münzwurf Zahl fällt und P(K_i) die Wahrscheinlichkeit, dass beim i-ten Münzwurf Kopf fällt. Man kommt genau dann zum k-ten Wurf, wenn man vorher k-1-mal Zahl geworfen hat. Also ist die Wahrscheinlichkeit, dass das erste Mal beim k-ten Münzwurf "Kopf" fällt:

$p_k=P(Z_1)\cdot P(Z_2)\dotsb P(Z_{k-1})\cdot P(K_k)=\frac{1}{2}\cdot\frac{1}{2}\dotsb\frac{1}{2}=\frac{1}{2^k}.$

Wieviel kann man im Durchschnitt erwarten zu gewinnen? Mit Wahrscheinlichkeit 1/2 ist der Gewinn 1 Euro, mit Wahrscheinlichkeit 1/4 ist er 2 Euro, mit Wahrscheinlichkeit 1/8 ist er 4 Euro etc. Der Erwartungswert ist daher

$E=\frac{1}{2}\cdot 1+\frac{1}{4}\cdot 2 + \frac{1}{8}\cdot 4 + \cdots =\sum_{k=1}^\infty p_k 2^{k-1} =\sum_{k=1}^\infty {1 \over 2}=\infty.$

(Σ bezeichnet eine Summierung, siehe Summenzeichen.) Diese Summe divergiert gegen unendlich; "im Durchschnitt" erwartet man daher einen unendlichen Gewinn.

Allerdings ist die Wahrscheinlichkeit, z.B. 1024 Euro oder mehr zu gewinnen sehr klein, nämlich gerade 1:1024. (1:2048 für 1024 Euro und 1:2048 für mehr)

Gemäß einer Entscheidungstheorie, die auf dem Erwartungswert basiert, sollte man daher jede beliebige Teilnahmegebühr akzeptieren. Dies widerspricht natürlich einer tatsächlichen Entscheidung, und scheint auch irrational zu sein, da man in der Regel nur einige Euro gewinnt. Diese offenbar paradoxe Diskrepanz führte zu dem Namen Sankt-Petersburg-Paradoxon.

Lösungen des Paradoxons

Es gibt mehrere Ansätze, dieses Paradoxon zu lösen.

Erwartungsnutzentheorie

Ökonomen nutzen dieses Paradoxon, um Konzepte in der Entscheidungstheorie zu demonstrieren. Das Paradox wird dabei gelöst, indem die naive Entscheidungstheorie, die auf dem Erwartungswert basiert, durch die (vernünftigere) Erwartungsnutzentheorie (Utility Theorie) ersetzt wird.

Diese Theorie des sinkenden Grenznutzens des Geldes wurde schon von Bernoulli erkannt. Die Hauptidee ist hierbei, dass ein Geldbetrag unterschiedlich bewertet wird: Zum Beispiel ist der relative Unterschied in der (subjektiven) Nützlichkeit von 2 Billionen Euro zu 1 Billion Euro sicher kleiner als der entsprechende Unterschied zwischen 1 Billion Euro und gar keinem Geld. Die Beziehung zwischen Geldwert und Nutzen ist also nicht-linear. Verallgemeinert man diese Idee, so hat eine 1:100'000'000'000 Chance, 100'000'000'000 Euro zu gewinnen, zwar einen Erwartungswert von einem Euro, muss aber nicht zwingend auch einen Euro wert sein.

Wenn wir nun eine Nutzenfunktion, wie zum Beispiel die von Bernoulli vorgeschlagene Logarithmusfunktion u(x)=ln(x), verwenden, so hat die Sankt-Petersburg-Lotterie einen endlichen Wert:

$EU=\sum_{k=1}^\infty p_k u(2^{k-1}) =\sum_{k=1}^\infty {\ln(2^{k-1}) \over {2^k}}= \ln 2 <\infty.$

In Bernoullis eigenen Worten:

"Die Berechnung des Wertes einer Sache darf nicht auf ihrem Preis basiert werden, sondern stattdessen auf die Nützlichkeit, die sie besitzt … Unzweifelhaft ist ein Gewinn von 1000 Dukaten für einen Bettler signifikanter als für einen Wohlhabenden, obgleich beide denselben Betrag erhalten."

Diese Lösung ist jedoch noch nicht vollauf befriedigend, da die Lotterie in einer Weise geändert werden kann, dass das Paradox wiederauftritt: Dazu müssen wir lediglich die Lotterie so ändern, dass die Auszahlungen 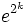$e^{2^k}$ betragen, dann ist der Wert der Lotterie, berechnet mit der logarithmischen Nutzenfunktionen, wieder unendlich.

Allgemein kann man für jede unbeschränkte Nutzenfunktion eine Variante des Sankt-Petersburg-Paradoxon finden, die einen unendlichen Wert liefert, wie von dem österreichischen Mathematiker Karl Menger als erstem bemerkt wurde.^[1]

Es gibt nun im Wesentlichen zwei Möglichkeiten, dieses neue Paradox, das zuweilen Super-Sankt-Petersburg-Paradox genannt wird, zu lösen:

• Man kann berücksichtigen, dass ein Kasino nur Lotterien mit einem endlichen Erwartungswert anbieten würde. Unter dieser Annahme lässt sich zeigen, dass das Paradox verschwindet, falls die Nutzenfunktion konkav ist, was bedeutet, dass man eine Risikoaversion (zumindest für hohe Geldbeträge) voraussetzt.^[2]

• Man kann annehmen, dass die Nutzenfunktion nach oben beschränkt ist. Dies bedeutet nicht, dass die Nutzenfunktion ab einem bestimmten Wert konstant sein muss. Als Beispiel betrachte u(x) = 1 − e ^{− x}.

In den letzten Jahren wurde die Expected Utility Theory erweitert, um Entscheidungsmodelle zu erhalten, die das reale Verhalten von Testpersonen quantitativ besser beschreiben. In einigen dieser neuen Theorien, wie zum Beispiel in Cumulative Prospect Theory, taucht das Sankt-Petersburg-Paradox in einigen Fällen auch dann auf, wenn die Nutzenfunktion konkav und der Erwartungswert endlich ist, jedoch nicht, wenn die Nutzenfunktion beschränkt ist.^[3]

Endliche Sankt-Petersburg-Lotterie

In der klassischen Variante der Sankt-Petersburg-Lotterie hat das Kasino unbegrenzte Geldvorräte. Es gibt also keinen Gewinn, den das Kasino nicht auszahlen könnte, und das Spiel könnte beliebig lange gehen.

Geht man hingegen von einem realen Kasino mit einem Kapital von K aus, dann kann das Kasino nicht mehr als einen maximalen Gewinn auszahlen. Erreicht der Spieler die daraus resultierende Grenze von N Münzwürfen, dann wird ihm der Gewinn an dieser Stelle ausgezahlt und das Spiel abgebrochen. Diese Grenze N legt das Kasino vorher fest.

Man erhält nun einen endlichen Erwartungswert. Zur Berechnung verwendet man die Formel

$E \ =\ \sum_{k=1}^N p_k 2^{k-1}+2^{N-1}\sum_{k=N+1}^\infty p_k\ =\ \sum_{k=1}^N{1 \over 2}+2^{N-1} \left(1-\left(1-{1 \over {2^N}}\right)\right)\ =\ {N+1 \over 2},$

mit N = 1 + [log₂(K)], wobei [X] die größte ganze Zahl kleiner oder gleich X bezeichnen soll.

Folgende Tabelle zeigt, welche Erwartungswerte die endliche Sankt-Petersburg-Lotterie für verschiedene Kasinotypen hat:

Kasinokapital K	max. Spiellänge N	Erwartungswert E
100 €	7	4 €	Spiel unter Freunden
100 Millionen €	27	14 €	(normales) Kasino
100 Milliarden €	37	19 €	Ungefährer EU-Haushalt 2005

Weblinks

Eine kurze Einführung in Utility Theorie und ihre Verbindung zum Sankt-Petersburg-Paradox findet sich hier:

• The New School for Social Research, New York, "The history of economic thought" (in Englisch)

Ein anregender, aber zuweilen nicht ganz korrekter Artikel aus Sicht eines Philosophen findet sich hier:

• Martin, Robert (2004), "The St. Petersburg Paradox". In The Stanford Encyclopaedia of Philosophy (Fall 2004 Edition), Edward N. Zalta (ed.) (auf Englisch)

Man kann die Sankt-Petersburg-Lotterie auch online spielen, allerdings ist dabei kein echtes Geld involviert:

• http://www.mathematik.com/Petersburg/Petersburg.html

Referenzen

Eine Übersetzung von Bernoullis Originalarbeit ins Englische:

• Bernoulli, Daniel (1738), "Exposition of a New Theory on the Measurement of Risk", Econometrica vol. 22 (1954), pp. 23-36 (Version im Internet: http://www.math.fau.edu/richman/Ideas/daniel.htm)

Der Briefwechsel von Nikolaus I. Bernoulli und Pierre Rémond de Montmort (englische Internetversion):

• http://www.cs.xu.edu/math/Sources/Montmort/stpetersburg.pdf

Ein Kommentar bezüglich beschränkter Nutzenfunktion und des St.-Petersburg-Paradox:

• Aumann, Robert J. (1977), "The St. Petersburg paradox: A discussion of some recent comments", Journal of Economic Theory, vol. 14, pp. 443-445

Im Text zitierte Artikel:

1. ↑ Menger, Karl (1934), "Das Unsicherheitsmoment in der Wertenlehre", Z. Nationalokon., vol. 51, pp. 459-485.
2. ↑ Vergleiche Arrow, Kenneth J. (1974), "The use of unbounded utility functions in expected-utility maximization: Response", Quarterly Journal of Economics, vol. 88, pp. 136-138.
3. ↑ Rieger, Marc Oliver and Wang, Mei (2006), "Cumulative prospect theory and the St. Petersburg paradox", Economic Theory, vol. 28, issue 3, pp. 665-679.