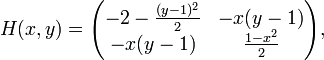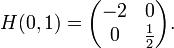- Sattelstelle
-
In der Mathematik bezeichnet man mit Sattelpunkt oder Terrassenpunkt einen kritischen Punkt einer Funktion, genauer eines Skalarfeldes, der kein Extremwert ist. Dieser Punkt ist ein Spezialfall des Wendepunktes.
Inhaltsverzeichnis
Eindimensionaler Fall
Für Funktionen einer Veränderlichen
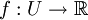 mit
mit 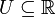 ist das Verschwinden der ersten Ableitung an der Stelle x0
ist das Verschwinden der ersten Ableitung an der Stelle x0- f'(x0) = 0
eine Bedingung dafür, dass ein kritischer Punkt vorliegt. Ist die 2. Ableitung an dieser Stelle nicht gleich 0, so liegt ein Extrempunkt und damit kein Sattelpunkt vor. Für einen Sattelpunkt muss also ebenfalls die 2. Ableitung 0 sein. Dies ist allerdings nur eine notwendige Bedingung, wie man an der Funktion f(x) = x4 sieht. Ist die 3. Ableitung ungleich 0, so liegt ein Sattelpunkt vor, es handelt sich also um einen Wendepunkt mit waagrechter Tangente. Genauer muss für gerades
 gelten:
gelten:Es sind also die ersten n Ableitungen gleich 0 und die (n + 1)-te Ableitung ungleich 0.
Mehrdimensionaler Fall
Spezifikation über Ableitungen
Für Funktionen mehrerer Veränderlichen
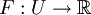 mit
mit 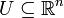 ist das Verschwinden des Gradienten an der Stelle x0
ist das Verschwinden des Gradienten an der Stelle x0eine Bedingung dafür, dass ein kritischer Punkt vorliegt. Ist zusätzlich die Hesse-Matrix indefinit, so liegt ein Sattelpunkt vor.
Spezifikation direkt über die Funktion
Für den Fall, dass der Sattelpunkt mit den Koordinatenachsen ausgerichtet ist, lässt sich ein Sattelpunkt auch ganz ohne Ableitungen in einfacher Weise beschreiben: Ein Punkt
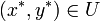 ist ein Sattelpunkt der Funktion F, falls
ist ein Sattelpunkt der Funktion F, fallsfür alle
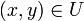 erfüllt ist. Anschaulich bedeutet dies, dass der Funktionswert von F in x-Richtung kleiner wird, sobald der Sattelpunkt verlassen wird, während ein Verlassen des Sattelpunktes in y-Richtung ein Ansteigen der Funktion F zur Folge hat. Diese Beschreibung eines Sattelpunktes ist Ursprung der Namensgebung: Ein Reitsattel neigt sich senkrecht zur Wirbelsäule des Pferdes nach unten, stellt also die x-Richtung dar, während er in y-Richtung, d.h. parallel zur Wirbelsäule, nach oben ausgeformt ist.
erfüllt ist. Anschaulich bedeutet dies, dass der Funktionswert von F in x-Richtung kleiner wird, sobald der Sattelpunkt verlassen wird, während ein Verlassen des Sattelpunktes in y-Richtung ein Ansteigen der Funktion F zur Folge hat. Diese Beschreibung eines Sattelpunktes ist Ursprung der Namensgebung: Ein Reitsattel neigt sich senkrecht zur Wirbelsäule des Pferdes nach unten, stellt also die x-Richtung dar, während er in y-Richtung, d.h. parallel zur Wirbelsäule, nach oben ausgeformt ist.Falls der Sattelpunkt nicht in Koordinatenrichtung ausgerichtet ist, stellt sich die obige Beziehung nach einer Koordinatentransformation ein.
Beispiel
Die Funktion
hat den Sattelpunkt (0,1): Ist y = 1, so ist
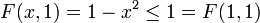 für alle
für alle 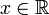 . Für x = 0 ergibt sich
. Für x = 0 ergibt sich 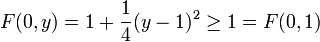 .
.Dass (0,1) ein Sattelpunkt von F ist, lässt sich auch über das Ableitungskriterium beweisen. Es ist
und nach Einsetzen von (x,y) = (0,1) ergibt sich
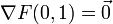 . Die Hesse-Matrix zu F ist
. Die Hesse-Matrix zu F istund nach Einsetzen des Sattelpunktes (x,y) = (0,1):
Da ein Eigenwert von H positiv ist (1 / 2) und einer negativ ( − 2), ist die Hesse-Matrix indefinit, was nachweist, dass tatsächlich ein Sattelpunkt vorliegt.
Siehe auch
Weblinks
Wikimedia Foundation.


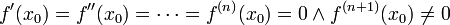
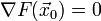
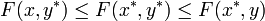
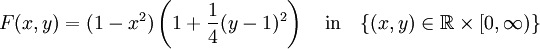
![\nabla F(x,y) = \left[-2x\left(1+\frac{1}{4}(y-1)^2\right),(1-x^2)\frac{y-1}{2}\right],](/pictures/dewiki/101/eca703cd6ff0e2483045b48430cd75fa.png)