- Satz von Bohr-Mollerup
-
Die Gammafunktion ist in der Mathematik eine Funktion, die definiert wird als
für x > 0. Sie genügt der Funktionalgleichung
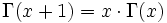 ,
,
aus der sich mit der Bedingung Γ(1) = 1 der Wert der Gammafunktion für alle positiven ganzen Zahlen n als
- Γ(n) = (n − 1)!
ergibt. Sie erweitert also die Fakultätsfunktion auf die positiven reellen Zahlen.
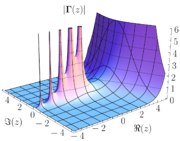
Die Gammafunktion lässt sich als meromorphe Funktion ohne Nullstellen auf die komplexe Zahlenebene mit einfachen Polstellen an den nichtpositiven ganzen Zahlen fortsetzen.
Aus der Gammafunktion leitet sich die Gamma-Wahrscheinlichkeitsverteilung ab.
Inhaltsverzeichnis
Darstellungsformen
Eine weitere Ausweitung des Definitionsbereichs erlaubt die Darstellung der Gammafunktion nach Gauß:
Direkt aus der Gaußschen Darstellungsform abgeleitet ist diejenige von Karl Weierstraß:
wobei die Eulersche Konstante γ definiert ist als
Näherungswerte der Gammafunktion für x > 0 liefert die Stirlingsche Formel, es gilt
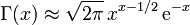 .
.
Der Satz von Bohr-Mollerup
Der Satz von Bohr-Mollerup (H. Bohr und J. Mollerup, 1922) erlaubt eine einfache Charakterisierung der Gammafunktion:
- Eine Funktion
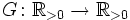 ist in diesem Bereich gleich der Gammafunktion, wenn folgende Eigenschaften erfüllt sind:
ist in diesem Bereich gleich der Gammafunktion, wenn folgende Eigenschaften erfüllt sind:
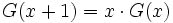
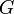 ist logarithmisch konvex, d.h.
ist logarithmisch konvex, d.h. 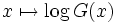 ist eine konvexe Funktion.
ist eine konvexe Funktion.
Die ersten beiden Bedingungen werden auch von Funktionen wie
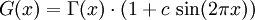 , 0 < c < 1, erfüllt.
, 0 < c < 1, erfüllt.Funktionalgleichungen
Die Gammafunktion genügt der Funktionalgleichung
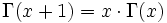 mit
mit 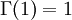 und
und 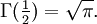
Der Ergänzungssatz der Gammafunktion
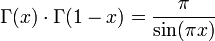 für
für 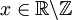
ermöglicht die Berechnung von Werten der Gammafunktion aus bereits bekannten Funktionswerten ebenso wie die Legendresche Verdopplungsformel
Diese ist ein Spezialfall der Gaußschen Multiplikationsformel
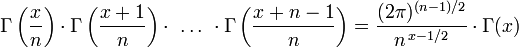 für
für 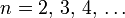
Zusammenhang zur Riemannschen ζ-Funktion
Die Gammafunktion besitzt folgende Beziehung zur Riemannschen ζ-Funktion, was von Riemann mit Hilfe der Funktionentheorie abgeleitet wurde.
Unvollständige Gammafunktion
In der Literatur wird dieser Begriff, im Hinblick auf Integrationsgrenzen und Normierung (Regularisierung), nicht einheitlich verwendet.
Häufige Notationen sind:
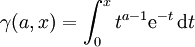 unvollständige Gammafunktion der oberen Grenze
unvollständige Gammafunktion der oberen Grenze
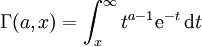 unvollständige Gammafunktion der unteren Grenze
unvollständige Gammafunktion der unteren Grenze
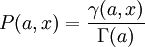 regularisierte (unvollständige) Gammafunktion der oberen Grenze
regularisierte (unvollständige) Gammafunktion der oberen Grenze
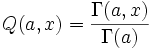 regularisierte (unvollständige) Gammafunktion der unteren Grenze
regularisierte (unvollständige) Gammafunktion der unteren Grenze
Spricht man von einer regularisierten Gammafunktion, so induziert dies schon, dass sie unvollständig ist.
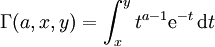 bzw.
bzw. 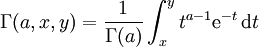
steht für die verallgemeinerte unvollständige Gammafunktion. Unklar ist, ob sie regularisiert ist oder nicht. Ebenso unklar ist, ob man das Wort "verallgemeinert" darauf beziehen soll, dass nun beide Integrationsgrenzen variabel sind, oder ob es sich, wie bei den obigen vier Darstellungen, um eine Verallgemeinerung der (vollständigen) Gammafunktion handelt.
Geschichtliches
1730 stellte Leonhard Euler in einem Brief an Christian Goldbach folgendes Integral zur Interpolation der Fakultätsfunktion vor:
(Diese Funktionsdefinition geht durch die Substitution u = ln(1 / t) in die obige Form über.)
Dieses Integral entdeckte Euler bei der Untersuchung eines Problems aus der Mechanik, bei dem die Beschleunigung eines Partikels betrachtet wird.
Die Verwendung des griechischen Gamma-Zeichens und die uns heute vertraute Darstellung wurde erst später durch Adrien-Marie Legendre eingeführt.
Siehe auch
Literatur
- Niels Nielsen: Handbuch der Theorie der Gammafunktion, Teubner, Leipzig 1906
- Emil Artin: Einführung in die Theorie der Gammafunktion (DjVu-Datei, 30 Sekunden Verzögerung), Teubner, Leipzig 1931
- Philip J. Davis: Leonhard Euler’s Integral: A Historic Profile of the Gamma Function. In: American Mathematical Monthly, Band 66, Jahrgang 1959, Seiten 849–869
- Konrad Königsberger: Analysis 1. Springer, Heidelberg 2003, ISBN 3-540-40371-X.
Weblinks
- Eric W. Weisstein: Gamma Function auf MathWorld (englisch)
- gamma function bei PlanetMath
Wikimedia Foundation.



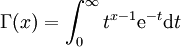
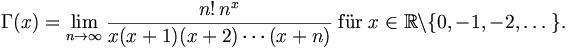
![\Gamma(x) = \left[ x \cdot \mathrm{e}^{\gamma x} \cdot \prod_{k=1}^{\infty} \left(1+\frac{x}{k}\right)\mathrm{e}^{-x/k} \right]^{-1},](/pictures/dewiki/48/08328fd43c2d478dd3deb14bad434712.png)
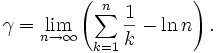
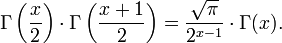
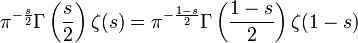
![\int_0^1 \left[\ln\left(\frac{1}{t}\right)\right]^{x-1} \mathrm{d}t](/pictures/dewiki/99/c31c2d0037fbc5a6b3fa4dc5e4510a61.png)