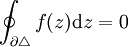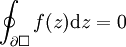Satz von Goursat

Das Lemma von Goursat, manchmal auch als Satz von Goursat bezeichnet, ist ein Satz aus der Funktionentheorie.

Das Lemma von Goursat ist eine Vorstufe des Cauchyschen Integralsatzes und wird auch oft für dessen Beweis genutzt. Es spielt im Aufbau der Funktionentheorie eine wichtige Rolle. Bemerkenswert ist, dass das Lemma lediglich die komplexe Differenzierbarkeit voraussetzt, nicht aber die stetige Differenzierbarkeit. Das Lemma wurde von Édouard Goursat (1858-1936) in der Rechteckform bewiesen und 1884 veröffentlicht. Die heute übliche Dreiecksform stammt von Alfred Pringsheim.

Das Lemma von Goursat

Das Lemma von Goursat für Dreiecke

Sei 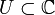$U \subset \mathbb{C}$ offen und 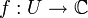$f: U \rightarrow \mathbb{C}$ holomorph (komplex-differenzierbar). Dann gilt für das Wegintegral längs der Randkurve 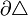$\partial \triangle$ eines jeden in U gelegenen Dreieckes $\triangle$:

$\oint_{\partial \triangle} f(z)\mathrm{d}z = 0$

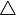Das Lemma von Goursat für Rechtecke

Manchmal wird das Lemma von Goursat auch für Rechtecke formuliert:

Sei 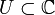$U \subset \mathbb{C}$ offen und 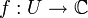$f: U \rightarrow \mathbb{C}$ holomorph. Dann gilt für alle Randkurven 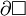$\partial \Box$ eines in U gelegenen Rechteckes $\Box$:

$\oint_{\partial \Box} f(z)\mathrm{d}z = 0$

Verschärfung des Lemmas von Goursat

Das Lemma von Goursat gilt auch mit etwas schwächeren Voraussetzungen:

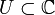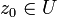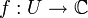Sei $U \subset \mathbb{C}$ offen, $z_0 \in U$ und $f: U \rightarrow \mathbb{C}$ stetig und holomorph auf 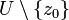$U \setminus \{z_0 \}$, dann gilt für alle Randkurven 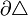$\partial \triangle$ von in U gelegenen Dreiecken 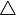$\triangle$ mit z₀ als Eckpunkt:

$\oint_{\partial \triangle} f(z)\mathrm{d}z = 0$