Satz von Routh

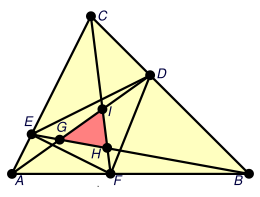
Der Satz von Routh, benannt nach Edward Routh, ist ein mathematischer Satz zur Geometrie des Dreiecks. Er macht folgende Aussage über den Flächeninhalt von Dreiecken (siehe Grafik):

ABC sei ein Dreieck mit Flächeninhalt A_ABC (äußeres Dreieck in der Grafik). Ferner seien F, D und E Punkte auf den Seiten [AB], [BC] bzw. [AC]. Die Teilverhältnisse seien:

$\overline{AF}/\overline{BF} = r$

$\overline{BD}/\overline{CD} = s$

$\overline{CE}/\overline{AE} = t$

Mit I, G und H seien die Schnittpunkte von AD und CF, AD und BE bzw. BE und CF bezeichnet.

Dann gilt für den Flächeninhalt von Dreieck GHI (inneres Dreieck in der Grafik):

$A_{GHI} = \frac{(rst-1)^2}{(st+s+1)(rt+t+1)(rs+r+1)} A_{ABC}.$

Der Satz von Ceva kann als Spezialfall des Satzes von Routh aufgefasst werden. Schneiden sich nämlich die Transversalen [AD], [BE] und [CF] in einem Punkt, so ist der Flächeninhalt des Dreiecks GHI gleich 0. Daraus kann rst = 1 gefolgert werden, also die Aussage des Satzes von Ceva.

Weblinks

• Beweis bei Schule.at

Literatur

• H. S. M. Coxeter: Introduction to Geometry, 2nd edition, Wiley, New York, 1969