- Teilverhältnis
-
Unter dem Teilverhältnis versteht man in der Geometrie eine Zahl, die die Position eines Punktes in Bezug auf eine gegebene Strecke festlegt. Als Formelzeichen wird häufig λ verwendet. Teilt der Punkt T die Strecke
![\left[ AB \right]](2/bc2cd38ffa8fdb466e9b0d2a102caf1d.png) , so schreibt man für das Teilverhältnis
, so schreibt man für das Teilverhältnis  oder, wenn die Bedeutung aus dem Zusammenhang klar ist, häufiger noch einfach λ = (ABT).
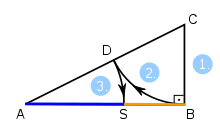
oder, wenn die Bedeutung aus dem Zusammenhang klar ist, häufiger noch einfach λ = (ABT). Beispiel für ein Teilverhältnis: Die Seitenhalbierende sa wird vom Schwerpunkt S des Dreiecks im Verhältnis 2:1 geteilt. Dabei wird die Seitenhalbierende von der Ecke A zur gegenüberliegenden Mitte Ma der Strecke a hin orientiert; formalisiert:
Beispiel für ein Teilverhältnis: Die Seitenhalbierende sa wird vom Schwerpunkt S des Dreiecks im Verhältnis 2:1 geteilt. Dabei wird die Seitenhalbierende von der Ecke A zur gegenüberliegenden Mitte Ma der Strecke a hin orientiert; formalisiert: .
.Die Mitte M einer Strecke teilt zum Beispiel die Strecke
![\left[ AB \right]](2/bc2cd38ffa8fdb466e9b0d2a102caf1d.png) im Verhältnis 1:1, d.h. λ = (ABM) = 1. Ein weiteres einfaches Beispiel ist die in der Abbildung dargestellte Aussage über den Schwerpunkt und die Seitenhalbierenden in einem beliebigen Dreieck.
im Verhältnis 1:1, d.h. λ = (ABM) = 1. Ein weiteres einfaches Beispiel ist die in der Abbildung dargestellte Aussage über den Schwerpunkt und die Seitenhalbierenden in einem beliebigen Dreieck.Ein (äußeres) Teilverhältnis wird zusätzlich für den Fall definiert, dass T nicht auf der Strecke
![\left[ AB \right]](2/bc2cd38ffa8fdb466e9b0d2a102caf1d.png) liegt, sondern auf deren Verlängerung (äußere Teilung). Zusammen ergeben inneres und äußeres Teilverhältnis den Begriff Teilverhältnis in der affinen Geometrie, mit dem eine wichtige Invariante unter affinen Abbildungen beschrieben werden kann. Dieses allgemeinere Teilverhältnis hängt eng mit affinen Koordinatensystemen zusammen: Affine Koordinaten können stets aus Teilverhältnissen berechnet werden und umgekehrt.
liegt, sondern auf deren Verlängerung (äußere Teilung). Zusammen ergeben inneres und äußeres Teilverhältnis den Begriff Teilverhältnis in der affinen Geometrie, mit dem eine wichtige Invariante unter affinen Abbildungen beschrieben werden kann. Dieses allgemeinere Teilverhältnis hängt eng mit affinen Koordinatensystemen zusammen: Affine Koordinaten können stets aus Teilverhältnissen berechnet werden und umgekehrt.Das Doppelverhältnis wird ähnlich gebildet wie das Teilverhältnis und hat in Projektiven Räumen eine vergleichbare Bedeutung.
Im Falle einer zweidimensionalen Geometrie (Ebene) wird ein Teilverhältnis in der synthetischen Geometrie allgemeiner auch für bestimmte nichtdesarguesche Ebenen definiert. → Siehe Affine Translationsebene.
Inhaltsverzeichnis
Elementargeometrische Definition
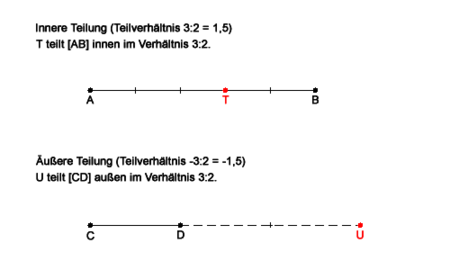
Innere Teilung
Gegeben seien eine Strecke [AB] und ein von B verschiedener Punkt T auf [AB]. Dann ist das Teilverhältnis definiert durch
Einfache Teilverhältnisse werden in der Regel als Brüche angegeben; statt λ = 1,5 schreibt man „Teilverhältnis 3:2“ und spricht dies „3 zu 2“.
Wenn T mit B zusammenfällt, kann man λ = ∞ festsetzen.
Äußere Teilung
Liegt T auf der Geraden AB, jedoch nicht auf der Strecke [AB], so ist
Bei einer äußeren Teilung ist das Teilverhältnis also stets eine negative Zahl. Statt „λ = −1,5“ sagt man jedoch in der Regel „T teilt [AB] außen im Verhältnis 3:2“
Vertauschung von A und B
Beim Teilverhältnis wird [AB] als „gerichtete Strecke“ aufgefasst; es wird also zwischen Anfangs- und Endpunkt der Strecke unterschieden. Teilt ein Punkt die Strecke [AB] im Teilverhältnis λ, so teilt er [BA] im Teilverhältnis 1/λ. Als Formel:
 für T ≠ A und T ≠ B
für T ≠ A und T ≠ B
Dies gilt für die innere wie auch für die äußere Teilung.
Zeichnerisches Ermitteln des Teilpunkts
Um den Teilpunkt zu finden, verwendet man eine Konstruktion nach dem zweiten Strahlensatz: Soll die Strecke [AB] im Verhältnis m:n geteilt werden, so zeichnet man durch A und durch B zwei parallele Geraden. Auf der Parallelen durch A trägt man m-mal, auf der Parallelen durch B n-mal die gleiche Strecke ab. Bei innerer Teilung muss das Abtragen in verschiedener Richtung, bei äußerer Teilung in gleicher Richtung erfolgen. Man zeichnet die Gerade durch die Endpunkte der abgetragenen Strecken. Ihr Schnittpunkt mit der Geraden AB ist der gesuchte Teilpunkt.
Einheitliche Definition des Teilverhältnisses
Die Fallunterscheidung in innere und äußere Teilung lässt sich dadurch vermeiden, dass man das Konzept der gerichteten Strecke verwendet und den Längen der gerichteten Strecken ein Vorzeichen zuschreibt: Der Wert von lg(AT) (gerichtete Streckenlänge) beziehungsweise lg(BT) soll negativ sein, wenn die entsprechende Strecke entgegengesetzt zu [AB] verläuft.
Mit dieser Festsetzung kann man (für T≠B) einheitlich definieren:
Die gerichteten Strecken können auch als Vektoren aufgefasst werden. Da für Vektoren der Quotient nicht definiert ist, setzt man dann fest:
Das Teilverhältnis des Punktes T bezüglich der Strecke [AB] ist die (für
 ) eindeutig bestimmte Zahl λ, für die gilt
) eindeutig bestimmte Zahl λ, für die gilt .
.
Eine einheitliche Darstellung erhält man ebenfalls, wenn AB eine Zahlengerade ist. Haben A, B und T die Zahlenwerte a, b und t (t≠b), so ist
 ,
,
und das Vorzeichen ergibt sich automatisch.
Sind die Punkte in einem Parallelkoordinatensystem gegeben durch A(a|a'), und B(b|b') und T(t|t'), so ist
 .
.
Die Teilverhältnisse der Koordinatenabschnitte sind also dieselben wie die auf der Geraden AB. Dies folgt aus dem ersten Strahlensatz.
Irrationale Teilverhältnisse
Nicht für jeden Teilpunkt T ist es möglich, das Teilverhältnis als ein Verhältnis ganzer Zahlen anzugeben. Dies herausgefunden zu haben ist eine hervorragende Leistung bereits der griechischen Mathematik. So ist zum Beispiel das Teilverhältnis beim goldenen Schnitt (λ = 1/2 + √5 /2) eine irrationale Zahl, die sich nicht in der Form m:n (mit ganzzahligem m und n) schreiben lässt.
Dagegen entspricht jedem Punkt T der Geraden AB (außer dem Punkt B) eine reelle Zahl als Teilverhältnis (ABT). Umgekehrt kann man sagen, dass die Teilverhältnisse (ABT), wenn T die Gerade AB durchwandert, alle reellen Zahlen und den Wert ∞ annehmen.
Das Teilverhältnis erzeugt also eine umkehrbar eindeutige Abbildung der (bei B gelochten) Gerade AB auf die Menge der reellen Zahlen. Nimmt man als Strecke [AB] das Intervall [0;1] der Zahlengeraden und als Teilpunkt den Punkt x, so entspricht dieser Abbildung der Funktionsterm
 .
.Rechnerische Bestimmung des Teilpunkts
Wenn die Strecke
![\left[ AB \right]](2/bc2cd38ffa8fdb466e9b0d2a102caf1d.png) und das Teilverhältnis
und das Teilverhältnis  , in dem T die Strecke teilt, gegeben sind, berechnet man die gerichtete Länge der Strecke
, in dem T die Strecke teilt, gegeben sind, berechnet man die gerichtete Länge der Strecke ![\left[ AT \right]](9/a1988b2d4fffc708b4aac1bb8cf444a0.png) nach der Formel
nach der FormelLiegt λ zwischen 0 und −1, so ergibt sich für lg(AT) ein negativer Wert. Tist dann auf der Seite der Verbindungsgeraden AB einzutragen, auf der (von A aus gesehen) B nicht liegt.
Die Gleichung kann man auch als Vektorgleichung für die Verbindungsvektoren lesen:
Teilverhältnis und affine Koordinaten
Sind die Punkte A(a | a') und B(b | b') der affinen Ebene durch ihre inhomogenen affinen Koordinaten gegeben, so sind die entsprechenden Koordinaten von T(t | t'):
 .
.
Analog können in affinen Räumen mit mehr als 2 Dimensionen alle inhomogenen Koordinaten von T aus den entsprechenden Koordinaten von A und B berechnet werden: Sind A und B durch ihre Ortsvektoren gegeben, dann ist
 der Ortsvektor von T.
der Ortsvektor von T.
Koordinatensysteme auf der Verbindungsgeraden, Geradengleichung
 Das Hebelgesetz an einer Wippe kann den Zusammenhang zwischen Teilverhältnis und baryzentrischen Koordinaten anschaulich machen: Wenn das Gewicht des linken Punktes A 20 mal so groß ist, wie das Gewicht des rechten Punktes B, teilt der Schwerpunkt, in dem die Wippe unterstützt werden muss, die Verbindungsstrecke (von A, dem Auflagepunkt des größeren Gewichts aus gesehen) im Verhältnis 1:20.
Das Hebelgesetz an einer Wippe kann den Zusammenhang zwischen Teilverhältnis und baryzentrischen Koordinaten anschaulich machen: Wenn das Gewicht des linken Punktes A 20 mal so groß ist, wie das Gewicht des rechten Punktes B, teilt der Schwerpunkt, in dem die Wippe unterstützt werden muss, die Verbindungsstrecke (von A, dem Auflagepunkt des größeren Gewichts aus gesehen) im Verhältnis 1:20.
Andererseits kann man auch auf der Verbindungsgeraden AB alleine ein affines Koordinatensystem mit Ursprung A und "Einheitspunkt" B einführen. Dann lässt sich der Ortsvektor eines beliebigen Punktes auf der Geraden eineindeutig durch einen Parameterwert τ in der Geradengleichung in Parameterform
 darstellen. Gleichwertig ist
darstellen. Gleichwertig ist 
Der Parameterwert τ ist dann die inhomogene affine Koordinate von T bezüglich des affinen Koordinatensystems (A,B). Ein Vergleich mit dem Teilverhältnis λ liefert die Umrechnungsformeln
 und
und 
In der baryzentrischen Darstellung gilt für den Ortsvektor
 eines Punktes T auf der Geraden AB:
eines Punktes T auf der Geraden AB:Hier ist das Teilverhältnis
 , die Koordinaten (λ0;λ1) sind die baryzentrischen Koordinaten von T bezüglich des Koordinatensystems (A,B). Das Bild rechts veranschaulicht ein Beispiel, in dem T der Schwerpunkt der beiden Massen auf der Wippe,
, die Koordinaten (λ0;λ1) sind die baryzentrischen Koordinaten von T bezüglich des Koordinatensystems (A,B). Das Bild rechts veranschaulicht ein Beispiel, in dem T der Schwerpunkt der beiden Massen auf der Wippe,  ,
,  ist - diese Zahlen können hier als relative Gewichte der Auflagepunkte auf der Wippe angesehen werden - und die Streckenteilung im umgekehrten Verhältnis zum Gewichtsverhältnis erfolgt: λ = 1:20.
ist - diese Zahlen können hier als relative Gewichte der Auflagepunkte auf der Wippe angesehen werden - und die Streckenteilung im umgekehrten Verhältnis zum Gewichtsverhältnis erfolgt: λ = 1:20.Invariante der Affinen Geometrie
Das Teilverhältnis ist eine Invariante jeder affinen Abbildung, d.h. es behält bei Anwendung einer solchen Abbildung (beispielsweise einer Spiegelung, einer zentrischen Streckung oder einer Scherung) seinen Wert, sofern nicht die ganze Gerade, auf der das Teilverhältnis berechnet wird, auf einen einzigen Punkt abgebildet wird. Die Eigenschaft kann als kennzeichnendes Merkmal der affinen Geometrie angesehen werden.
→ Die Beschreibung einer "Geometrie" durch ihre Invarianten wird im Hauptartikel Erlanger Programm dargelegt.
Siehe auch
Weblinks
Literatur
- Hermann Schaal, Ekkehart Glässner: Lineare Algebra und analytische Geometrie, Band 1, 255 Seiten, Vieweg; Braunschweig, Wiesbaden 1976, ISBN 3-528-03056-9
- Uwe Storch, Hartmut Wiebe: Lehrbuch der Mathematik, Band II: Lineare Algebra. BI-Wissenschafts-Verlag, 1990, ISBN 3-411-14101-8
Wikimedia Foundation.